信号处理 (scipy.signal)

信号处理工具箱目前包含一些滤波函数、一组有限的滤波器设计工具以及一些用于 1-D 和 2-D 数据的 B 样条插值算法。虽然 B 样条算法在技术上可以归类为插值，但它们之所以包含在此处，是因为它们仅适用于等间距数据，并且大量使用滤波理论和传递函数形式来提供快速 B 样条变换。要理解本节，你需要了解 SciPy 中的信号是一个实数或复数数组。

B 样条

B 样条是对有限域上的连续函数的一种近似，其通过 B 样条系数和节点来表示。如果节点等间距，间距为 \(\Delta x\)，则 1-D 函数的 B 样条近似是有限基展开。

\[y\left(x\right)\approx\sum_{j}c_{j}\beta^{o}\left(\frac{x}{\Delta x}-j\right).\]

在具有节点间距 \(\Delta x\) 和 \(\Delta y\) 的二维情况下，函数表示为

\[z\left(x,y\right)\approx\sum_{j}\sum_{k}c_{jk}\beta^{o}\left(\frac{x}{\Delta x}-j\right)\beta^{o}\left(\frac{y}{\Delta y}-k\right).\]

在这些表达式中，\(\beta^{o}\left(\cdot\right)\) 是 \(o\) 阶空间有限 B 样条基函数。等间距节点和等间距数据点的要求使得可以开发快速（逆滤波）算法，从样本值 \(y_{n}\) 确定系数 \(c_{j}\)。与通用样条插值算法不同，这些算法可以快速找到大型图像的样条系数。

通过 B 样条基函数表示一组样本的优点在于，连续域算子（导数、重采样、积分等），它们假定数据样本来自底层连续函数，可以相对容易地从样条系数计算。例如，样条的二阶导数是

\[y{}^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\beta^{o\prime\prime}\left(\frac{x}{\Delta x}-j\right).\]

利用 B 样条的性质

\[\frac{d^{2}\beta^{o}\left(w\right)}{dw^{2}}=\beta^{o-2}\left(w+1\right)-2\beta^{o-2}\left(w\right)+\beta^{o-2}\left(w-1\right),\]

可以看出

\[y^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\left[\beta^{o-2}\left(\frac{x}{\Delta x}-j+1\right)-2\beta^{o-2}\left(\frac{x}{\Delta x}-j\right)+\beta^{o-2}\left(\frac{x}{\Delta x}-j-1\right)\right].\]

如果 \(o=3\)，则在样本点处

\begin{eqnarray*} \Delta x^{2}\left.y^{\prime}\left(x\right)\right|_{x=n\Delta x} & = & \sum_{j}c_{j}\delta_{n-j+1}-2c_{j}\delta_{n-j}+c_{j}\delta_{n-j-1},\\ & = & c_{n+1}-2c_{n}+c_{n-1}.\end{eqnarray*}

因此，二阶导数信号可以很容易地从样条拟合中计算出来。如果需要，可以找到平滑样条以使二阶导数对随机误差不那么敏感。

精明的读者可能已经注意到，数据样本通过卷积运算符与节点系数相关联，因此与采样 B 样条函数的简单卷积可以从样条系数中恢复原始数据。卷积的输出可能会根据边界处理方式而变化（随着数据集中维度的增加，这一点变得越来越重要）。信号处理子包中与 B 样条相关的算法假定镜像对称边界条件。因此，样条系数是基于该假设计算的，并且数据样本可以通过假定它们也镜像对称来从样条系数中精确恢复。

目前，该包提供了用于确定一维和二维等间距样本的二阶和三阶立方样条系数的函数（qspline1d、qspline2d、cspline1d、cspline2d）。对于较大的 \(o\)，B 样条基函数可以通过标准差等于 \(\sigma_{o}=\left(o+1\right)/12\) 的零均值高斯函数很好地近似

\[\beta^{o}\left(x\right)\approx\frac{1}{\sqrt{2\pi\sigma_{o}^{2}}}\exp\left(-\frac{x^{2}}{2\sigma_{o}}\right).\]

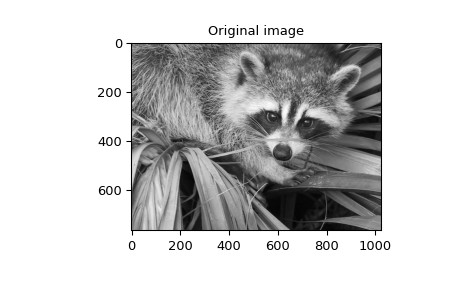
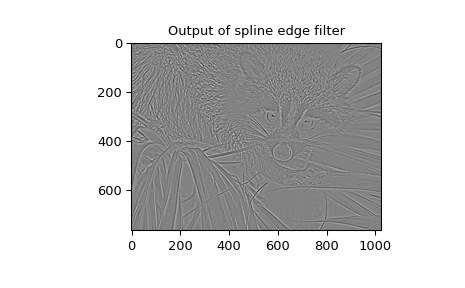
一个用于计算任意 \(x\) 和 \(o\) 的高斯函数的函数也可用（gauss_spline）。以下代码和图使用样条滤波来计算浣熊脸的边缘图像（平滑样条的二阶导数），这是命令 scipy.datasets.face 返回的数组。命令 sepfir2d 用于对样条系数应用具有镜像对称边界条件的可分离二维 FIR 滤波器。此函数非常适合从样条系数重建样本，并且比 convolve2d 更快，后者卷积任意二维滤波器并允许选择镜像对称边界条件。

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True).astype(np.float32)
>>> derfilt = np.array([1.0, -2, 1.0], dtype=np.float32)
>>> ck = signal.cspline2d(image, 8.0)
>>> deriv = (signal.sepfir2d(ck, derfilt, [1]) +
...          signal.sepfir2d(ck, [1], derfilt))

或者，我们可以这样做

laplacian = np.array([[0,1,0], [1,-4,1], [0,1,0]], dtype=np.float32)
deriv2 = signal.convolve2d(ck,laplacian,mode='same',boundary='symm')

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(deriv)
>>> plt.gray()
>>> plt.title('Output of spline edge filter')
>>> plt.show()

滤波

滤波是对输入信号进行某种修改的任何系统的通用名称。在 SciPy 中，信号可以被认为是 NumPy 数组。不同类型的操作有不同类型的滤波器。滤波操作主要有两种：线性和非线性。线性滤波器总是可以归结为将展平的 NumPy 数组乘以适当的矩阵，从而得到另一个展平的 NumPy 数组。当然，这通常不是计算滤波器的最佳方法，因为所涉及的矩阵和向量可能非常大。例如，用这种方法滤波一个 \(512 \times 512\) 图像将需要一个 \(512^2 \times 512^2\) 矩阵与一个 \(512^2\) 向量相乘。仅仅尝试使用标准 NumPy 数组存储 \(512^2 \times 512^2\) 矩阵将需要 \(68,719,476,736\) 个元素。以每个元素 4 字节计算，这将需要 \(256\textrm{GB}\) 内存。在大多数应用中，该矩阵的大多数元素都是零，因此采用不同的方法来计算滤波器的输出。

卷积/相关

许多线性滤波器还具有移不变性。这意味着滤波操作在信号的不同位置是相同的，并且它意味着滤波矩阵可以仅通过矩阵的一行（或一列）的信息来构建。在这种情况下，矩阵乘法可以通过傅里叶变换来完成。

设 \(x\left[n\right]\) 定义一个由整数 \(n\) 索引的 1-D 信号。两个 1-D 信号的完全卷积可以表示为

\[y\left[n\right]=\sum_{k=-\infty}^{\infty}x\left[k\right]h\left[n-k\right].\]

这个方程只能在我们将序列限制为可以存储在计算机中的有限支持序列，选择 \(n=0\) 作为两个序列的起始点，让 \(K+1\) 是所有 \(n\geq K+1\) 的 \(x\left[n\right]=0\) 的值，并且 \(M+1\) 是所有 \(n\geq M+1\) 的 \(h\left[n\right]=0\) 的值时直接实现，然后离散卷积表达式为

\[y\left[n\right]=\sum_{k=\max\left(n-M,0\right)}^{\min\left(n,K\right)}x\left[k\right]h\left[n-k\right].\]

为方便起见，假设 \(K\geq M.\) 那么，更明确地，此操作的输出是

\begin{eqnarray*} y\left[0\right] & = & x\left[0\right]h\left[0\right]\\ y\left[1\right] & = & x\left[0\right]h\left[1\right]+x\left[1\right]h\left[0\right]\\ y\left[2\right] & = & x\left[0\right]h\left[2\right]+x\left[1\right]h\left[1\right]+x\left[2\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[M\right] & = & x\left[0\right]h\left[M\right]+x\left[1\right]h\left[M-1\right]+\cdots+x\left[M\right]h\left[0\right]\\ y\left[M+1\right] & = & x\left[1\right]h\left[M\right]+x\left[2\right]h\left[M-1\right]+\cdots+x\left[M+1\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[K\right] & = & x\left[K-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[0\right]\\ y\left[K+1\right] & = & x\left[K+1-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[1\right]\\ \vdots & \vdots & \vdots\\ y\left[K+M-1\right] & = & x\left[K-1\right]h\left[M\right]+x\left[K\right]h\left[M-1\right]\\ y\left[K+M\right] & = & x\left[K\right]h\left[M\right].\end{eqnarray*}

因此，两个长度分别为 \(K+1\) 和 \(M+1\) 的有限序列的完全离散卷积，其结果是一个长度为 \(K+M+1=\left(K+1\right)+\left(M+1\right)-1\) 的有限序列。

1-D 卷积在 SciPy 中通过函数 convolve 实现。此函数将信号 \(x,\) \(h\) 作为输入，以及两个可选标志“mode”和“method”，并返回信号 \(y.\)

第一个可选标志“mode”允许指定返回输出信号的哪个部分。默认值“full”返回整个信号。如果该标志的值为“same”，则只返回中间的 \(K\) 个值，从 \(y\left[\left\lfloor \frac{M-1}{2}\right\rfloor \right]\) 开始，这样输出的长度与第一个输入相同。如果该标志的值为“valid”，则只返回中间的 \(K-M+1=\left(K+1\right)-\left(M+1\right)+1\) 个输出值，其中 \(z\) 取决于最小输入的所有值，从 \(h\left[0\right]\) 到 \(h\left[M\right].\) 换句话说，只返回包括 \(y\left[M\right]\) 到 \(y\left[K\right]\) 的值。

第二个可选标志“method”决定了如何计算卷积，可以通过傅里叶变换方法（使用 fftconvolve）或通过直接方法。默认情况下，它会选择预期更快速的方法。傅里叶变换方法的时间复杂度为 \(O(N\log N)\)，而直接方法的时间复杂度为 \(O(N^2)\)。根据大 O 常数和 \(N\) 的值，这两种方法之一可能更快。默认值“auto”会进行粗略计算并选择预期更快速的方法，而值“direct”和“fft”则强制使用另外两种方法进行计算。

以下代码展示了两个序列卷积的简单示例

>>> x = np.array([1.0, 2.0, 3.0])
>>> h = np.array([0.0, 1.0, 0.0, 0.0, 0.0])
>>> signal.convolve(x, h)
array([ 0.,  1.,  2.,  3.,  0.,  0.,  0.])
>>> signal.convolve(x, h, 'same')
array([ 2.,  3.,  0.])

同样，函数 convolve 实际上可以接受 N-D 数组作为输入，并返回两个数组的 N-D 卷积，如下面的代码示例所示。在这种情况下，同样可以使用相同的输入标志。

>>> x = np.array([[1., 1., 0., 0.], [1., 1., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]])
>>> h = np.array([[1., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 0.]])
>>> signal.convolve(x, h)
array([[ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]])

相关与卷积非常相似，只是负号变成了正号。因此，

\[w\left[n\right]=\sum_{k=-\infty}^{\infty}y\left[k\right]x\left[n+k\right],\]

是信号 \(y\) 和 \(x\) 的（互）相关。对于有限长信号，当 \(y\left[n\right]=0\) 在范围 \(\left[0,K\right]\) 之外，且 \(x\left[n\right]=0\) 在范围 \(\left[0,M\right]\) 之外时，求和可以简化为

\[w\left[n\right]=\sum_{k=\max\left(0,-n\right)}^{\min\left(K,M-n\right)}y\left[k\right]x\left[n+k\right].\]

再次假设 \(K\geq M\)，则结果为

\begin{eqnarray*} w\left[-K\right] & = & y\left[K\right]x\left[0\right]\\ w\left[-K+1\right] & = & y\left[K-1\right]x\left[0\right]+y\left[K\right]x\left[1\right]\\ \vdots & \vdots & \vdots\\ w\left[M-K\right] & = & y\left[K-M\right]x\left[0\right]+y\left[K-M+1\right]x\left[1\right]+\cdots+y\left[K\right]x\left[M\right]\\ w\left[M-K+1\right] & = & y\left[K-M-1\right]x\left[0\right]+\cdots+y\left[K-1\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[-1\right] & = & y\left[1\right]x\left[0\right]+y\left[2\right]x\left[1\right]+\cdots+y\left[M+1\right]x\left[M\right]\\ w\left[0\right] & = & y\left[0\right]x\left[0\right]+y\left[1\right]x\left[1\right]+\cdots+y\left[M\right]x\left[M\right]\\ w\left[1\right] & = & y\left[0\right]x\left[1\right]+y\left[1\right]x\left[2\right]+\cdots+y\left[M-1\right]x\left[M\right]\\ w\left[2\right] & = & y\left[0\right]x\left[2\right]+y\left[1\right]x\left[3\right]+\cdots+y\left[M-2\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[M-1\right] & = & y\left[0\right]x\left[M-1\right]+y\left[1\right]x\left[M\right]\\ w\left[M\right] & = & y\left[0\right]x\left[M\right].\end{eqnarray*}

SciPy 函数 correlate 实现了此操作。此操作同样提供了等效的标志，用于返回完整的 \(K+M+1\) 长度序列（“full”）或与最长序列大小相同的序列，从 \(w\left[-K+\left\lfloor \frac{M-1}{2}\right\rfloor \right]\) 开始（“same”），或返回其值取决于最短序列所有值的序列（“valid”）。此最后一个选项返回包括 \(w\left[M-K\right]\) 到 \(w\left[0\right]\) 的 \(K-M+1\) 个值。

函数 correlate 也可以将任意 N-D 数组作为输入，并输出两个数组的 N-D 卷积。

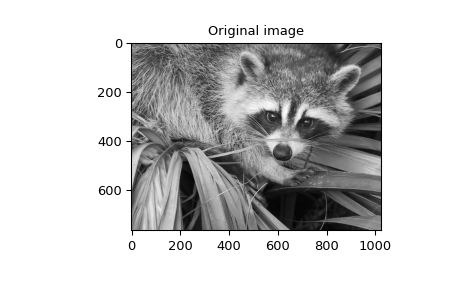
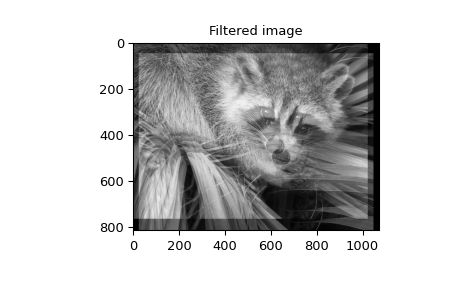
当 \(N=2,\) correlate 和/或 convolve 可用于构建任意图像滤波器，以执行图像的模糊、增强和边缘检测等操作。

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True)
>>> w = np.zeros((50, 50))
>>> w[0][0] = 1.0
>>> w[49][25] = 1.0
>>> image_new = signal.fftconvolve(image, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

如上所述在时域中计算卷积主要用于其中一个信号远小于另一个信号（\(K\gg M\)）的滤波情况，否则线性滤波在频域中计算效率更高，由函数 fftconvolve 提供。默认情况下，convolve 使用 choose_conv_method 估计最快的方法。

如果滤波器函数 \(w[n,m]\) 可以分解为

\[h[n, m] = h_1[n] h_2[m],\]

则卷积可以通过函数 sepfir2d 来计算。举个例子，我们考虑一个高斯滤波器 gaussian

\[h[n, m] \propto e^{-x^2-y^2} = e^{-x^2} e^{-y^2},\]

这通常用于模糊处理。

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = np.asarray(datasets.ascent(), np.float64)
>>> w = signal.windows.gaussian(51, 10.0)
>>> image_new = signal.sepfir2d(image, w, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

差分方程滤波

一类通用线性 1-D 滤波器（包括卷积滤波器）是通过差分方程描述的滤波器

\[\sum_{k=0}^{N}a_{k}y\left[n-k\right]=\sum_{k=0}^{M}b_{k}x\left[n-k\right],\]

其中 \(x\left[n\right]\) 是输入序列，\(y\left[n\right]\) 是输出序列。如果我们假设初始状态为静止，即 \(y\left[n\right]=0\) 对于 \(n<0\)，那么这种滤波器可以使用卷积来实现。然而，如果 \(a_{k}\neq0\) 对于 \(k\geq1,\) 则卷积滤波器序列 \(h\left[n\right]\) 可能是无限的。此外，这类通用线性滤波器允许在 \(n<0\) 时对 \(y\left[n\right]\) 施加初始条件，从而导致无法用卷积表示的滤波器。

差分方程滤波器可以被认为是递归地根据其先前值来寻找 \(y\left[n\right]\)

\[a_{0}y\left[n\right]=-a_{1}y\left[n-1\right]-\cdots-a_{N}y\left[n-N\right]+\cdots+b_{0}x\left[n\right]+\cdots+b_{M}x\left[n-M\right].\]

通常，选择 \(a_{0}=1\) 进行归一化。SciPy 中此通用差分方程滤波器的实现比上述方程所暗示的要复杂一些。它被实现为只需要延迟一个信号。实际的实现方程是（假设 \(a_{0}=1\)）

\begin{eqnarray*} y\left[n\right] & = & b_{0}x\left[n\right]+z_{0}\left[n-1\right]\\ z_{0}\left[n\right] & = & b_{1}x\left[n\right]+z_{1}\left[n-1\right]-a_{1}y\left[n\right]\\ z_{1}\left[n\right] & = & b_{2}x\left[n\right]+z_{2}\left[n-1\right]-a_{2}y\left[n\right]\\ \vdots & \vdots & \vdots\\ z_{K-2}\left[n\right] & = & b_{K-1}x\left[n\right]+z_{K-1}\left[n-1\right]-a_{K-1}y\left[n\right]\\ z_{K-1}\left[n\right] & = & b_{K}x\left[n\right]-a_{K}y\left[n\right],\end{eqnarray*}

其中 \(K=\max\left(N,M\right).\) 请注意，如果 \(K>M\)，则 \(b_{K}=0\)；如果 \(K>N,\) 则 \(a_{K}=0.\) 通过这种方式，时间 \(n\) 的输出仅取决于时间 \(n\) 的输入和前一时刻 \(z_{0}\) 的值。只要在每个时间步计算并存储 \(K\) 个值 \(z_{0}\left[n-1\right]\ldots z_{K-1}\left[n-1\right]\)，就可以始终计算出这个值。

差分方程滤波器通过 SciPy 中的命令 lfilter 调用。此命令将向量 \(b,\) 向量 \(a,\) 信号 \(x\) 作为输入，并返回使用上述方程计算的向量 \(y\)（与 \(x\) 长度相同）。如果 \(x\) 是 N-D 数组，则滤波器将沿提供的轴计算。如果需要，可以提供初始条件来给出 \(z_{0}\left[-1\right]\) 到 \(z_{K-1}\left[-1\right]\) 的值，否则将假定它们都为零。如果提供了初始条件，则还会返回中间变量的最终条件。例如，这些条件可用于在相同状态下重新开始计算。

有时，以信号 \(x\left[n\right]\) 和 \(y\left[n\right]\) 的形式表达初始条件更为方便。换句话说，也许你已经有了 \(x\left[-M\right]\) 到 \(x\left[-1\right]\) 的值以及 \(y\left[-N\right]\) 到 \(y\left[-1\right]\) 的值，并且希望确定应将 \(z_{m}\left[-1\right]\) 的哪些值作为初始条件传递给差分方程滤波器。不难证明，对于 \(0\leq m<K,\)

\[z_{m}\left[n\right]=\sum_{p=0}^{K-m-1}\left(b_{m+p+1}x\left[n-p\right]-a_{m+p+1}y\left[n-p\right]\right).\]

使用此公式，我们可以根据 \(y\)（和 \(x\)）的初始条件找到初始条件向量 \(z_{0}\left[-1\right]\) 到 \(z_{K-1}\left[-1\right]\)。命令 lfiltic 执行此功能。

举个例子，考虑以下系统

\[y[n] = \frac{1}{2} x[n] + \frac{1}{4} x[n-1] + \frac{1}{3} y[n-1]\]

此代码计算给定信号 \(x[n]\) 的信号 \(y[n]\)；首先是初始条件 \(y[-1] = 0\)（默认情况），然后是 \(y[-1] = 2\)，通过 lfiltic 实现。

>>> import numpy as np
>>> from scipy import signal

>>> x = np.array([1., 0., 0., 0.])
>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.lfilter(b, a, x)
array([0.5, 0.41666667, 0.13888889, 0.0462963])
>>> zi = signal.lfiltic(b, a, y=[2.])
>>> signal.lfilter(b, a, x, zi=zi)
(array([ 1.16666667,  0.63888889,  0.21296296,  0.07098765]), array([0.02366]))

请注意，输出信号 \(y[n]\) 的长度与输入信号 \(x[n]\) 的长度相同。

线性系统分析

由线性差分方程描述的线性系统可以完全由系数向量 \(a\) 和 \(b\) 来描述，如上所述；另一种表示方法是提供一个因子 \(k\)、\(N_z\) 个零点 \(z_k\) 和 \(N_p\) 个极点 \(p_k\)，分别通过其传递函数 \(H(z)\) 来描述系统，如下所示：

\[H(z) = k \frac{ (z-z_1)(z-z_2)...(z-z_{N_z})}{ (z-p_1)(z-p_2)...(z-p_{N_p})}.\]

这种替代表示可以通过 scipy 函数 tf2zpk 获得；逆变换由 zpk2tf 提供。

对于上述示例，我们有

>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.tf2zpk(b, a)
(array([-0.5]), array([ 0.33333333]), 0.5)

即，系统在 \(z=-1/2\) 处有一个零点，在 \(z=1/3\) 处有一个极点。

SciPy 函数 freqz 允许计算由系数 \(a_k\) 和 \(b_k\) 描述的系统的频率响应。有关全面的示例，请参阅 freqz 函数的帮助文档。

滤波器设计

时域离散滤波器可分为有限脉冲响应（FIR）滤波器和无限脉冲响应（IIR）滤波器。FIR 滤波器可以提供线性相位响应，而 IIR 滤波器不能。SciPy 提供了用于设计这两种类型滤波器的函数。

FIR 滤波器

函数 firwin 根据窗函数法设计滤波器。根据提供的参数，函数会返回不同类型的滤波器（例如，低通、带通等）。

以下示例分别设计了一个低通滤波器和一个带阻滤波器。

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b1 = signal.firwin(40, 0.5)
>>> b2 = signal.firwin(41, [0.3, 0.8])
>>> w1, h1 = signal.freqz(b1)
>>> w2, h2 = signal.freqz(b2)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w1, 20*np.log10(np.abs(h1)), 'b')
>>> plt.plot(w2, 20*np.log10(np.abs(h2)), 'r')
>>> plt.ylabel('Amplitude Response (dB)')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

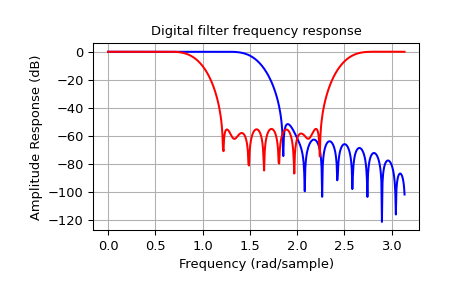
请注意，firwin 默认使用归一化频率，其中值 \(1\) 对应于奈奎斯特频率，而函数 freqz 定义中值 \(\pi\) 对应于奈奎斯特频率。

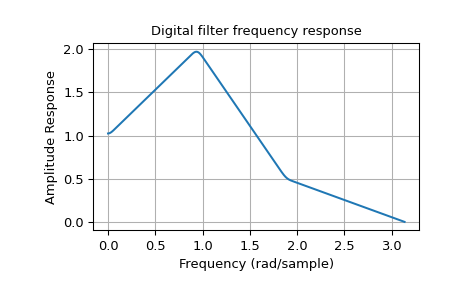
函数 firwin2 允许通过指定角频率数组和相应的增益来设计几乎任意的频率响应。

以下示例设计了一个具有此类任意幅度响应的滤波器。

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b = signal.firwin2(150, [0.0, 0.3, 0.6, 1.0], [1.0, 2.0, 0.5, 0.0])
>>> w, h = signal.freqz(b)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, np.abs(h))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

请注意 Y 轴的线性刻度以及 firwin2 和 freqz 中奈奎斯特频率的不同定义（如上所述）。

IIR 滤波器

SciPy 提供了两个函数来直接设计 IIR 滤波器：iirdesign 和 iirfilter，其中滤波器类型（例如，椭圆滤波器）作为参数传入；此外还有几个特定滤波器类型的设计函数，例如 ellip。

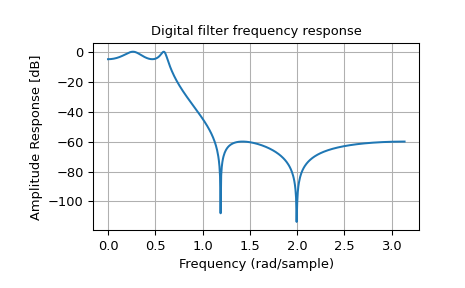
以下示例设计了一个具有定义通带和阻带波纹的椭圆低通滤波器。请注意，与上述 FIR 滤波器示例相比，为了达到约 \(60\) dB 的相同阻带衰减，该滤波器的阶数（4 阶）要低得多。

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirfilter(4, Wn=0.2, rp=5, rs=60, btype='lowpass', ftype='ellip')
>>> w, h = signal.freqz(b, a)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

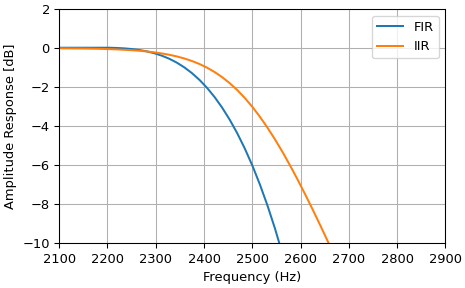
注意

需要注意的是，firwin 和 iirfilter 的截止频率定义不同。firwin 的截止频率在半幅度处（即 -6dB）。iirfilter 的截止频率在半功率处（即 -3dB）。

>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from scipy import signal as sig

>>> fs = 16000
>>> b = sig.firwin(101, 2500, fs=fs)
>>> f, h_fft = sig.freqz(b, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> _, ax = plt.subplots(layout="constrained")
>>> ax.plot(f, h_amp, label="FIR")
>>> ax.grid(True)

>>> b, a = sig.iirfilter(15, 2500, btype="low", fs=fs)
>>> f, h_fft = sig.freqz(b, a, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> ax.plot(f, h_amp, label="IIR")
>>> ax.set(xlim=[2100, 2900], ylim=[-10, 2])
>>> ax.set(xlabel="Frequency (Hz)", ylabel="Amplitude Response [dB]")
>>> ax.legend()

滤波器系数

滤波器系数可以以多种不同的格式存储

• “ba”或“tf”= 传递函数系数

• “zpk”= 零点、极点和总增益

• “ss”= 状态空间系统表示

• “sos”= 二阶节的传递函数系数

函数，例如 tf2zpk 和 zpk2ss，可以在它们之间进行转换。

传递函数表示

ba 或 tf 格式是一个 2 元组 (b, a)，表示一个传递函数，其中 b 是一个长度为 M+1 的数组，表示 M 阶分子多项式的系数，a 是一个长度为 N+1 的数组，表示 N 阶分母多项式的系数，按传递函数变量的降幂排列。因此，\(b = [b_0, b_1, ..., b_M]\) 和 \(a =[a_0, a_1, ..., a_N]\) 的元组可以表示模拟滤波器，形式为

\[H(s) = \frac {b_0 s^M + b_1 s^{(M-1)} + \cdots + b_M} {a_0 s^N + a_1 s^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i s^{(M-i)}} {\sum_{i=0}^N a_i s^{(N-i)}}\]

或离散时间滤波器，形式为

\[H(z) = \frac {b_0 z^M + b_1 z^{(M-1)} + \cdots + b_M} {a_0 z^N + a_1 z^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i z^{(M-i)}} {\sum_{i=0}^N a_i z^{(N-i)}}.\]

这种“正幂”形式在控制工程中更为常见。如果 M 和 N 相等（所有通过双线性变换生成的滤波器都如此），那么这恰好等同于 DSP 中更常用的“负幂”离散时间形式

\[H(z) = \frac {b_0 + b_1 z^{-1} + \cdots + b_M z^{-M}} {a_0 + a_1 z^{-1} + \cdots + a_N z^{-N}} = \frac {\sum_{i=0}^M b_i z^{-i}} {\sum_{i=0}^N a_i z^{-i}}.\]

尽管这对于常见滤波器是正确的，但请记住，在一般情况下并非如此。如果 M 和 N 不相等，离散时间传递函数系数必须首先转换为“正幂”形式，然后才能找到极点和零点。

这种表示在高阶时存在数值误差，因此在可能的情况下优先选择其他格式。

零点和极点表示

zpk 格式是一个 3 元组 (z, p, k)，其中 z 是一个长度为 M 的数组，表示传递函数的复零点 \(z = [z_0, z_1, ..., z_{M-1}]\)，p 是一个长度为 N 的数组，表示传递函数的复极点 \(p = [p_0, p_1, ..., p_{N-1}]\)，而 k 是一个标量增益。它们表示数字传递函数

\[H(z) = k \cdot \frac {(z - z_0) (z - z_1) \cdots (z - z_{(M-1)})} {(z - p_0) (z - p_1) \cdots (z - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (z - z_i)} {\prod_{i=0}^{N-1} (z - p_i)}\]

或模拟传递函数

\[H(s) = k \cdot \frac {(s - z_0) (s - z_1) \cdots (s - z_{(M-1)})} {(s - p_0) (s - p_1) \cdots (s - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (s - z_i)} {\prod_{i=0}^{N-1} (s - p_i)}.\]

尽管根集以有序 NumPy 数组的形式存储，但它们的顺序并不重要：([-1, -2], [-3, -4], 1) 与 ([-2, -1], [-4, -3], 1) 是相同的滤波器。

状态空间系统表示

ss 格式是一个由四个数组组成的元组 (A, B, C, D)，表示一个 N 阶数字/离散时间系统的状态空间，形式为

\[\begin{split}\mathbf{x}[k+1] = A \mathbf{x}[k] + B \mathbf{u}[k]\\ \mathbf{y}[k] = C \mathbf{x}[k] + D \mathbf{u}[k]\end{split}\]

或连续/模拟系统，形式为

\[\begin{split}\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)\\ \mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t),\end{split}\]

具有 P 个输入、Q 个输出和 N 个状态变量，其中

• x 是状态向量

• y 是长度为 Q 的输出向量

• u 是长度为 P 的输入向量

• A 是状态矩阵，形状为 (N, N)

• B 是输入矩阵，形状为 (N, P)

• C 是输出矩阵，形状为 (Q, N)

• D 是直通或前馈矩阵，形状为 (Q, P)。（在系统没有直接前馈的情况下，D 中的所有值都为零。）

状态空间是最通用的表示形式，也是唯一允许多输入、多输出（MIMO）系统的表示形式。对于给定的传递函数，存在多种状态空间表示。具体而言，“可控规范形式”和“可观测规范形式”与 tf 表示具有相同的系数，因此存在相同的数值误差。

二阶节表示

sos 格式是一个形状为 (n_sections, 6) 的二维数组，表示一系列二阶传递函数，当它们串联级联时，可以实现具有最小数值误差的高阶滤波器。每一行对应一个二阶 tf 表示，前三列提供分子系数，后三列提供分母系数

\[[b_0, b_1, b_2, a_0, a_1, a_2]\]

系数通常进行归一化，使得 \(a_0\) 始终为 1。在浮点计算中，节的顺序通常不重要；无论顺序如何，滤波器输出都将相同。

滤波器变换

IIR 滤波器设计函数首先生成一个原型模拟低通滤波器，其归一化截止频率为 1 弧度/秒。然后使用以下替换将其转换为其他频率和频带类型

类型	转换
lp2lp	\(s \rightarrow \frac{s}{\omega_0}\)
lp2hp	\(s \rightarrow \frac{\omega_0}{s}\)
lp2bp	\(s \rightarrow \frac{s^2 + {\omega_0}^2}{s \cdot \mathrm{BW}}\)
lp2bs	\(s \rightarrow \frac{s \cdot \mathrm{BW}}{s^2 + {\omega_0}^2}\)

这里，\(\omega_0\) 是新的截止或中心频率，\(\mathrm{BW}\) 是带宽。这些变换在对数频率轴上保持对称性。

为了将变换后的模拟滤波器转换为数字滤波器，使用了 bilinear 变换，它进行以下替换

\[s \rightarrow \frac{2}{T} \frac{z - 1}{z + 1},\]

其中 T 是采样时间（采样频率的倒数）。

其他滤波器

信号处理包还提供了许多其他滤波器。

中值滤波器

当中值滤波适用于噪声明显非高斯或需要保留边缘时。中值滤波器的工作原理是，对感兴趣点周围矩形区域中的所有数组像素值进行排序。此邻域像素值列表的样本中值用作输出数组的值。样本中值是排序后的邻域值列表中的中间数组值。如果邻域中元素的数量为偶数，则使用中间两个值的平均值作为中值。一个适用于 N-D 数组的通用中值滤波器是 medfilt。一个仅适用于 2-D 数组的专用版本是 medfilt2d。

阶数滤波器

中值滤波器是更通用的一类滤波器（称为阶数滤波器）的特定示例。为了计算特定像素的输出，所有阶数滤波器都使用该像素周围区域中的数组值。这些数组值经过排序，然后其中一个被选作输出值。对于中值滤波器，使用数组值列表的样本中值作为输出。通用阶数滤波器允许用户选择排序后的邻居数组值列表中的哪个元素将用作输出。因此，例如，可以选择选择列表中的最大值或最小值。阶数滤波器除了输入数组和区域掩码之外，还接受一个附加参数，该参数指定应使用排序后的邻居数组值列表中的哪个元素作为输出。执行阶数滤波器的命令是 order_filter。

维纳滤波器

维纳滤波器是一种简单的图像去模糊滤波器，用于图像去噪。这并非图像重建问题中常见的维纳滤波器，而是一种简单的局部均值滤波器。设 \(x\) 为输入信号，则输出为

\[\begin{split}y=\left\{ \begin{array}{cc} \frac{\sigma^{2}}{\sigma_{x}^{2}}m_{x}+\left(1-\frac{\sigma^{2}}{\sigma_{x}^{2}}\right)x & \sigma_{x}^{2}\geq\sigma^{2},\\ m_{x} & \sigma_{x}^{2}<\sigma^{2},\end{array}\right.\end{split}\]

其中 \(m_{x}\) 是均值的局部估计，\(\sigma_{x}^{2}\) 是方差的局部估计。这些估计的窗口是一个可选输入参数（默认为 \(3\times3\)）。参数 \(\sigma^{2}\) 是一个阈值噪声参数。如果未给出 \(\sigma\)，则将其估计为局部方差的平均值。

希尔伯特滤波器

希尔伯特变换从实信号构造复值解析信号。例如，如果 \(x=\cos\omega n\)，则 \(y=\textrm{hilbert}\left(x\right)\) 将返回（除了靠近边缘的部分） \(y=\exp\left(j\omega n\right).\) 在频域中，希尔伯特变换执行

\[Y=X\cdot H,\]

其中 \(H\) 对于正频率为 \(2\)，对于负频率为 \(0\)，对于零频率为 \(1\)。

模拟滤波器设计

函数 iirdesign、iirfilter 和特定滤波器类型的设计函数（例如 ellip）都带有一个标志 analog，它也允许设计模拟滤波器。

以下示例设计了一个模拟 (IIR) 滤波器，通过 tf2zpk 获得其零点和极点，并在复 s 平面中绘制它们。在幅度响应中可以清楚地看到 \(\omega \approx 150\) 和 \(\omega \approx 300\) 处的零点。

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirdesign(wp=100, ws=200, gpass=2.0, gstop=40., analog=True)
>>> w, h = signal.freqs(b, a)

>>> plt.title('Analog filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency')
>>> plt.grid()
>>> plt.show()

>>> z, p, k = signal.tf2zpk(b, a)

>>> plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
>>> plt.plot(np.real(p), np.imag(p), 'xr')
>>> plt.legend(['Zeros', 'Poles'], loc=2)

>>> plt.title('Pole / Zero Plot')
>>> plt.xlabel('Real')
>>> plt.ylabel('Imaginary')
>>> plt.grid()
>>> plt.show()

\[% LaTeX Macros to make the LaTeX formulas more readable: \newcommand{\IC}{{\mathbb{C}}} % set of complex numbers \newcommand{\IN}{{\mathbb{N}}} % set of natural numbers \newcommand{\IR}{{\mathbb{R}}} % set of real numbers \newcommand{\IZ}{{\mathbb{Z}}} % set of integers \newcommand{\jj}{{\mathbb{j}}} % imaginary unit \newcommand{\e}{\operatorname{e}} % Euler's number \newcommand{\dd}{\operatorname{d}} % infinitesimal operator \newcommand{\abs}[1]{\left|#1\right|} % absolute value \newcommand{\conj}[1]{\overline{#1}} % complex conjugate \newcommand{\conjT}[1]{\overline{#1^T}} % transposed complex conjugate \newcommand{\inv}[1]{\left(#1\right)^{\!-1}} % inverse % Since the physics package is not loaded, we define the macros ourselves: \newcommand{\vb}[1]{\mathbf{#1}} % vectors and matrices are bold % new macros: \newcommand{\rect}{\operatorname{rect}} % rect or boxcar function \newcommand{\sinc}{\operatorname{sinc}} % sinc(t) := sin(pi*t) / (pi*t)\]

频谱分析

频谱分析是指研究信号的傅里叶变换[1]。根据上下文，傅里叶变换的各种频谱表示有不同的名称，例如频谱、谱密度或周期图。[2] 本节以固定持续时间的连续时间正弦波信号为例，说明最常见的表示。然后讨论离散傅里叶变换[3] 在该正弦波的采样版本上的应用。

单独的小节专门讨论频谱的相位，估算功率谱密度（无平均periodogram和有平均welch），以及非等间距信号（lombscargle）。

请注意，傅里叶级数的概念密切相关，但有一个关键区别：傅里叶级数的频谱由离散频率谐波组成，而本节中的频谱在频率上是连续的。

连续时间正弦信号

考虑一个振幅为 \(a\)、频率为 \(f_x\)、持续时间为 \(\tau\) 的正弦信号，即

(1)\[x(t) = a \sin(2 \pi f_x t)\, \rect(\frac{t}{\tau}-\frac{1}{2}) = \left(\frac{a}{2\jj} \e^{\jj 2 \pi f_x t} - \frac{a}{2\jj} \e^{-\jj 2 \pi f_x t} \right) \rect(\frac{t}{\tau}-\frac{1}{2})\ .\]

由于 \(\rect(t)\) 函数在 \(|t|<1/2\) 时为 1，在 \(|t|>1/2\) 时为 0，因此它将 \(x(t)\) 限制在区间 \([0, \tau]\)。通过复指数表示正弦函数显示了其两个频率为 \(\pm f_x\) 的周期分量。我们假设 \(x(t)\) 是一个电压信号，因此其单位为 \(\text{V}\)。

在信号处理中，绝对值平方 \(|x(t)|^2\) 的积分用于定义信号的能量和功率，即

(2)\[E_x := \int_0^\tau |x(t)|^2 \dd t\ = \frac{1}{2}|a|^2\tau\ , \qquad P_x := \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ .\]

功率 \(P_x\) 可以解释为单位时间间隔内的能量 \(E_x\)。从单位来看，对 \(t\) 积分的结果是乘以秒。因此，\(E_x\) 的单位是 \(\text{V}^2\text{s}\)，\(P_x\) 的单位是 \(\text{V}^2\)。

对 \(x(t)\) 应用傅里叶变换，即

(3)\[X(f) = \int_{\IR} x(t)\, \e^{-2\jj\pi f t}\, \dd t = \frac{a \tau}{2\jj} \Big( \sinc\!\big(\tau (f-f_x)\big) - \sinc\!\big(\tau (f+f_x)\big) \Big)\e^{-\jj\pi\tau f}\ ,\]

结果是两个以 \(\pm f_x\) 为中心的 \(\sinc(f) := \sin(\pi f) /(\pi f)\) 函数。幅度（绝对值） \(|X(f)|\) 在 \(\pm f_x\) 处有两个最大值，其值为 \(|a|\tau/2\)。从下面的图中可以看出，\(X(f)\) 并非集中在 \(\pm f_x\) 处的主瓣周围，而是包含高度与 \(1/(\tau f)\) 成比例下降的旁瓣。这种所谓的“频谱泄漏”[4] 是由于将正弦函数限制在有限区间内造成的。请注意，信号持续时间 \(\tau\) 越短，泄漏越高。为了独立于信号持续时间，可以使用所谓的“幅度谱” \(X(f)/\tau\) 代替频谱 \(X(f)\)。其在 \(f\) 处的值对应于复指数 \(\exp(\jj2\pi f t)\) 的幅度。

根据帕塞瓦尔定理，能量也可以通过其傅里叶变换 \(X(f)\) 计算得到：

(4)\[ E_X := \int_\IR \abs{X(f)}^2 \dd f = E_x\]

同样。例如，通过直接计算可以证明方程 (4) 中 \(X(f)\) 的能量为 \(|a|^2\tau/2\)。因此，信号在频带 \(f_a, f_b\) 中的功率可以用以下方式确定

(5)\[P_X^{a,b} = \frac{1}{\tau} \int_{f_a}^{f_b} \abs{X(f)}^2 \dd f\ .\]

因此，函数 \(|X(f)|^2\) 可以定义为所谓的“能量谱密度”，而 \(S_{xx}(f) := |X(f)|^2 / \tau\) 可以定义为 \(x(t)\) 的“功率谱密度”（PSD）。除了 PSD 之外，还可以使用所谓的“幅度谱密度” \(X(f) / \sqrt{\tau}\)，它仍然包含相位信息。它的绝对值平方就是 PSD，因此它与信号的均方根（RMS）值 \(\sqrt{P_x}\) 的概念密切相关。

总而言之，本小节介绍了五种表示频谱的方法

正弦信号 \(x(t)\) （如方程 (1) 所示，单位为 \(\text{V}\)）的频谱表示比较：

	频谱	幅度谱	能量谱密度	功率谱密度 (PSD)	幅度谱密度
定义	\(X(f)\)	\(X(f) / \tau\)	\(|X(f)|^2\)	\(|X(f)|^2 / \tau\)	\(X(f) / \sqrt{\tau}\)
在 \(\pm f_x\) 处的幅度	\(\frac{1}{2}|a|\tau\)	\(\frac{1}{2}|a|\)	\(\frac{1}{4}|a|^2\tau^2\)	\(\frac{1}{4}|a|^2\tau\)	\(\frac{1}{2}|a|\sqrt{\tau}\)
单位	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

请注意，上表中给出的单位并非明确的，例如，\(\text{V}^2\text{s} / \text{Hz} = \text{V}^2\text{s}^2 = \text{V}^2/ \text{Hz}^2\)。当使用幅度谱的 \(|X(f) / \tau|\) 的绝对值时，它被称为幅度谱。此外，请注意，表示的命名方案不一致，在文献中各不相同。

对于实值信号，通常使用所谓的“单边”频谱表示。它只使用非负频率（因为如果 \(x(t)\in\IR\)，则 \(X(-f)= \conj{X}(f)\)）。有时，负频率的值会加到其对应的正频率上。然后，幅度谱允许读取 \(x(t)\) 在 \(f_x\) 处的完整（而非半）幅度正弦值，而 PSD 中一个区间的面积则表示其完整（而非半）功率。请注意，对于幅度谱密度，正值不加倍，而是乘以 \(\sqrt{2}\)，因为它是 PSD 的平方根。此外，对于加倍的频谱，没有规范的命名方式。

以下图表展示了四个正弦信号 \(x(t)\)（由方程式 (1) 定义，具有不同振幅 \(a\) 和持续时间 \(\tau\)）的三种不同频谱表示。为了减少混乱，频谱以 \(f_x\) 为中心并相邻绘制

import matplotlib.pyplot as plt
import numpy as np

aa = [1, 1, 2, 2]  # amplitudes
taus = [1, 2, 1, 2]  # durations

fg0, axx = plt.subplots(3, 1, sharex='all', tight_layout=True, figsize=(6., 4.))
axx[0].set(title=r"Spectrum $|X(f)|$", ylabel="V/Hz")
axx[1].set(title=r"Magnitude Spectrum $|X(f)/\tau|$ ", ylabel=r"V")
axx[2].set(title=r"Amplitude Spectral Density $|X(f)/\sqrt{\tau}|$",
           ylabel=r"$\operatorname{V} / \sqrt{\operatorname{Hz}}$",
           xlabel="Frequency $f$ in Hertz",)

x_labels, x_ticks = [], []
f = np.linspace(-2.5, 2.5, 400)
for c_, (a_, tau_) in enumerate(zip(aa, taus), start=1):
    aZ_, f_ = abs(a_ * tau_ * np.sinc(tau_ * f) / 2), f + c_ * 5
    axx[0].plot(f_, aZ_)
    axx[1].plot(f_, aZ_ / tau_)
    axx[2].plot(f_, aZ_ / np.sqrt(tau_))
    x_labels.append(rf"$a={a_:g}$, $\tau={tau_:g}$")
    x_ticks.append(c_ * 5)

axx[2].set_xticks(x_ticks)
axx[2].set_xticklabels(x_labels)
plt.show()

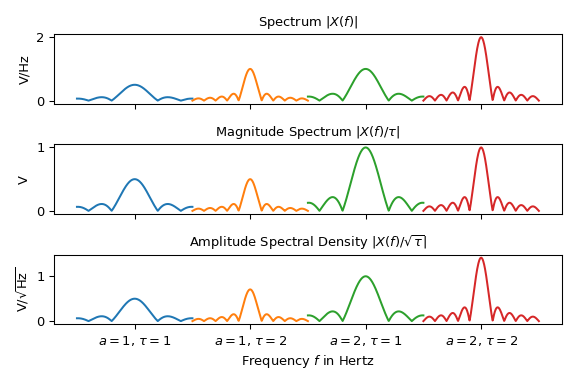
请注意，峰值的高度会根据表示方式而异。只有幅度谱的解释是直截了当的：第二个图中的 \(f_x\) 处的峰值代表正弦信号幅度的二分之一 \(|a|\)。对于所有其他表示，需要考虑持续时间 \(\tau\) 才能提取有关信号幅度信息。

采样正弦信号

在实践中，采样信号被广泛使用。即，信号由 \(n\) 个样本 \(x_k := x(kT)\)，\(k=0, \ldots, n-1\) 表示，其中 \(T\) 是采样间隔，\(\tau:=nT\) 是信号的持续时间，\(f_S := 1/T\) 是采样频率。请注意，连续信号需要被限制在 \([-f_S/2, f_S/2]\) 带宽内，以避免混叠，其中 \(f_S/2\) 被称为奈奎斯特频率。[5] 将积分替换为求和以计算信号的能量和功率，即

\[E_x = T\sum_{k=0}^{n-1} \abs{x_k}^2 = \frac{1}{2}|a|^2\tau\ , \qquad P_x = \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ ,\]

这与连续时间情况下方程 (2) 的结果相同。离散傅里叶变换 (DFT) 及其逆变换（通过 scipy.fft 模块中高效的 FFT 计算实现）由下式给出

(6)\[X_l := \sum_{k=0}^{n-1} x_k \e^{-2\jj\pi k l / n}\ ,\qquad x_k = \frac{1}{n} \sum_{l=0}^{n-1} X_l \e^{2\jj\pi k l / n}\ .\]

DFT 可以解释为方程 (3) 中连续傅里叶变换的未缩放采样版本，即

\[X(l\Delta f) = T X_l\ , \quad \Delta f := 1/\tau = 1/(nT)\ .\]

下图显示了两个单位振幅、频率分别为 20 Hz 和 20.5 Hz 的正弦信号的幅度谱。该信号由 \(n=100\) 个样本组成，采样间隔为 \(T=10\) 毫秒，导致持续时间为 \(\tau=1\) 秒，采样频率为 \(f_S=100\) Hz。

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
fcc = (20, 20.5)  # frequencies of sines
t = np.arange(n) * T
xx = (np.sin(2 * np.pi * fx_ * t) for fx_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided magnitude spectrum

fg1, ax1 = plt.subplots(1, 1, tight_layout=True, figsize=(6., 3.))
ax1.set(title=r"Magnitude Spectrum (no window) of $x(t) = \sin(2\pi f_x t)$ ",
        xlabel=rf"Frequency $f$ in Hertz (bin width $\Delta f = {f[1]}\,$Hz)",
        ylabel=r"Magnitude $|X(f)|/\tau$", xlim=(f[0], f[-1]))
for X_, fc_, m_ in zip(XX, fcc, ('x-', '.-')):
    ax1.plot(f, abs(X_), m_, label=rf"$f_x={fc_}\,$Hz")

ax1.grid(True)
ax1.legend()
plt.show()

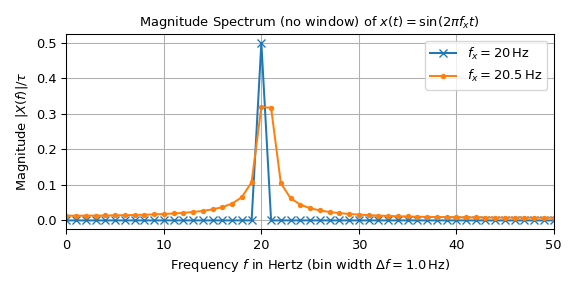
20 Hz 信号的解释似乎是直截了当的：除了 20 Hz 之外，所有值都为零。在那里，它为 0.5，这与输入信号幅度的一半相对应，符合方程 (1)。另一方面，20.5 Hz 信号的峰值沿频率轴分散。方程 (3) 表明这种差异是由于 20 Hz 是 1 Hz 仓宽的倍数而 20.5 Hz 不是造成的。下图通过将连续频谱叠加在采样频谱上来阐明这一点

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = (np.sin(2 * np.pi * fc_ * t) for fc_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided FFT normalized to magnitude

i0, i1 = 15, 25
f_cont = np.linspace(f[i0], f[i1], 501)

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, fx_) in enumerate(zip(axx, XX, fcc)):
    Xc_ = (np.sinc(tau * (f_cont - fx_)) +
           np.sinc(tau * (f_cont + fx_))) / 2
    ax_.plot(f_cont, abs(Xc_), f'-C{c_}', alpha=.5, label=rf"$f_x={fx_}\,$Hz")
    m_line, _, _, = ax_.stem(f[i0:i1+1], abs(X_[i0:i1+1]), markerfmt=f'dC{c_}',
                             linefmt=f'-C{c_}', basefmt=' ')
    plt.setp(m_line, markersize=5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f[i0], f[i1]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle("Continuous and Sampled Magnitude Spectrum ", x=0.55, y=0.93)
fg1.tight_layout()
plt.show()

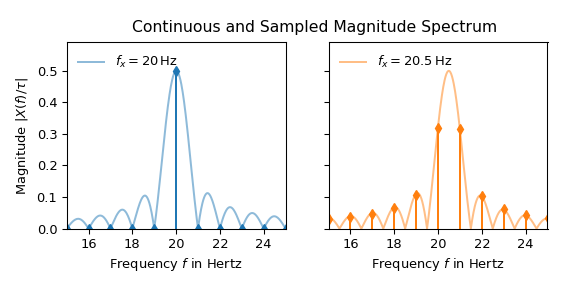
频率的微小变化会产生显著不同的幅度谱，这对于许多实际应用来说显然是不希望的行为。以下两种常用技术可以用来改进频谱

所谓的“零填充”通过在信号末尾附加零来减小 \(\Delta f\)。为了对频率进行 q 倍过采样，将参数 n=q*n_x 传递给 fft / rfft 函数，其中 n_x 是输入信号的长度。

第二种技术称为窗化，即用一个合适的函数乘以输入信号，从而通常会抑制旁瓣，但代价是加宽主瓣。加窗 DFT 可以表示为

(7)\[X^w_l := \sum_{k=0}^{n-1} x_k w_k\e^{-2\jj\pi k l / n}\ ,\]

其中 \(w_k\)，\(k=0,\ldots,n-1\) 是采样窗函数。为了计算前一小节中给出的频谱表示的采样版本，需要使用以下归一化常数

\[c^\text{amp}:= \abs{\sum_{k=0}^{n-1} w_k}\ ,\qquad c^\text{den} := \sqrt{\sum_{k=0}^{n-1} \abs{w_k}^2}\]

需要被利用。第一个确保频谱中的峰值与该频率下的信号幅度一致。例如，幅度谱可以用 \(|X^w_l / c^\text{amp}|\) 表示。第二个常数保证频率区间的功率与方程 (5) 中定义的功率一致。需要绝对值是因为不禁止复值窗口。

下图显示了对 \(x(t)\) 应用 hann 窗并进行三次过采样的结果

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal.windows import hann

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
q = 3  # over-sampling factor
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = [np.sin(2 * np.pi * fc_ * t) for fc_ in fcc]  # sine signals
w = hann(n)
c_w = abs(sum(w))  # normalize constant for window

f_X = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_ * w) / c_w for x_ in xx)  # one-sided amplitude spectrum
# Oversampled spectrum:
f_Y = rfftfreq(n*q, T)  # frequency bins range from 0 Hz to Nyquist freq.
YY = (rfft(x_ * w, n=q*n) / c_w for x_ in xx)  # one-sided magnitude spectrum

i0, i1 = 15, 25
j0, j1 = i0*q, i1*q

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, Y_, fx_) in enumerate(zip(axx, XX, YY, fcc)):
    ax_.plot(f_Y[j0:j1 + 1], abs(Y_[j0:j1 + 1]), f'.-C{c_}',
             label=rf"$f_x={fx_}\,$Hz")
    m_ln, s_ln, _, = ax_.stem(f_X[i0:i1 + 1], abs(X_[i0:i1 + 1]), basefmt=' ',
                              markerfmt=f'dC{c_}', linefmt=f'-C{c_}')
    plt.setp(m_ln, markersize=5)
    plt.setp(s_ln, alpha=0.5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f_X[15], f_X[25]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle(rf"Magnitude Spectrum (Hann window, ${q}\times$oversampled)",
             x=0.55, y=0.93)
plt.show()

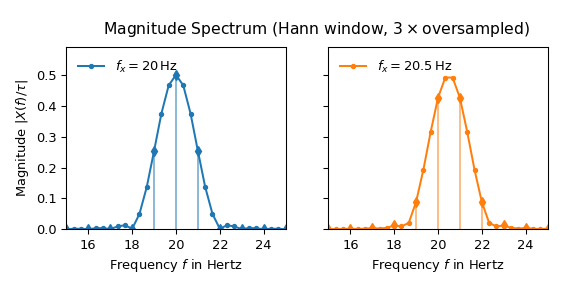
现在两个波瓣看起来几乎相同，并且旁瓣得到了很好的抑制。20.5 Hz 频谱的最大值也非常接近预期的一半高度。

频谱能量和频谱功率的计算类似于方程 (4)，得到相同的结果，即

\[E^w_X = T\sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = E_x\ ,\qquad P^w_X = \frac{1}{\tau} E^w_X = \frac{1}{n} \sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = P_x\ .\]

这个公式不要与矩形窗（或无窗）的特殊情况混淆，即 \(w_k = 1\)，\(X^w_l=X_l\)，\(c^\text{den}=\sqrt{n}\)，这导致

\[E_X = \frac{T}{n}\sum_{k=0}^{n-1} \abs{X_k}^2\ ,\qquad P_X = \frac{1}{n^2} \sum_{k=0}^{n-1} \abs{X_k}^2\ .\]

加窗频率离散功率谱密度

\[S^w_{xx} := \frac{1}{f_S}\abs{\frac{X^w_l}{c^\text{den}}}^2 = T \abs{\frac{X^w_l}{c^\text{den}}}^2\]

定义在频率范围 \([0, f_S)\) 上，可以解释为每频率间隔 \(\Delta f\) 的功率。对频率带 \(l_a\Delta f, l_b\Delta f)\) 求积分，如方程 (5) 所示，变为求和

\[P_X^{a,b} = \Delta f\sum_{k=l_a}^{l_b-1} S^w_{xx} = \frac{1}{nT}\sum_{k=l_a}^{l_b-1} S^w_{xx}\ .\]

加窗频率离散能量谱密度 \(\tau S^w_{xx}\) 可以类似地定义。

上述讨论表明，可以定义与连续时间情况中相同的频谱表示的采样版本。下表总结了这些

窗化 DFT \(X^w_l\)（如方程 (7) 所示）的频谱表示比较，适用于单位为 \(\text{V}\) 的采样信号：

	频谱	幅度谱	能量谱密度	功率谱密度 (PSD)	幅度谱密度
定义	\(\tau X^w_l / c^\text{amp}\)	\(X^w_l / c^\text{amp}\)	\(\tau T |X^w_l / c^\text{den}|^2\)	\(T |X^w_l / c^\text{den}|^2\)	\(\sqrt{T} X^w_l / c^\text{den}\)
单位	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

请注意，对于密度，\(\pm f_x\) 处的幅度值与连续时间情况不同，这是由于确定频谱能量/功率时将积分改为求和。

尽管汉宁窗（Hann window）是频谱分析中最常用的窗函数，但也存在其他窗函数。下图显示了windows子模块中各种窗函数的幅度谱。它可以被解释为单频率输入信号的瓣形。请注意，图中仅显示了右半部分，并且\(y\)轴以分贝表示，即按对数比例缩放。

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal import get_window

n, n_zp = 128, 16384  # number of samples without and with zero-padding
t = np.arange(n)
f = rfftfreq(n_zp, 1 / n)

ww = ['boxcar', 'hann', 'hamming', 'tukey', 'blackman', 'flattop']
fg0, axx = plt.subplots(len(ww), 1, sharex='all', sharey='all', figsize=(6., 4.))
for c_, (w_name_, ax_) in enumerate(zip(ww, axx)):
    w_ = get_window(w_name_, n, fftbins=False)
    W_ = rfft(w_ / abs(sum(w_)), n=n_zp)
    W_dB = 20*np.log10(np.maximum(abs(W_), 1e-250))
    ax_.plot(f, W_dB, f'C{c_}-', label=w_name_)
    ax_.text(0.1, -50, w_name_, color=f'C{c_}', verticalalignment='bottom',
             horizontalalignment='left', bbox={'color': 'white', 'pad': 0})
    ax_.set_yticks([-20, -60])
    ax_.grid(axis='x')

axx[0].set_title("Spectral Leakage of various Windows")
fg0.supylabel(r"Normalized Magnitude $20\,\log_{10}|W(f)/c^\operatorname{amp}|$ in dB",
              x=0.04, y=0.5, fontsize='medium')
axx[-1].set(xlabel=r"Normalized frequency $f/\Delta f$ in bins",
            xlim=(0, 9), ylim=(-75, 3))

fg0.tight_layout(h_pad=0.4)
plt.show()

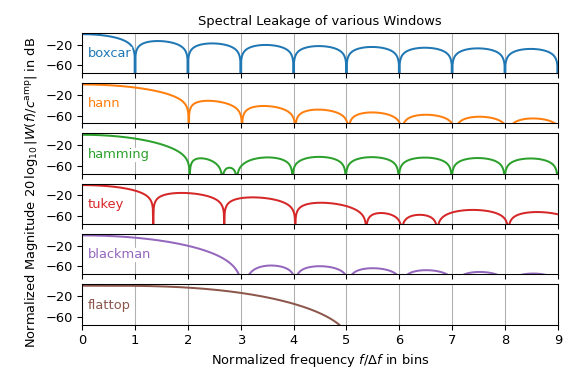
此图表明，窗函数的选择通常是主瓣宽度和旁瓣高度之间的权衡。请注意，boxcar窗对应于一个\(\rect\)函数，即没有加窗。此外，许多所示的窗函数在滤波器设计中比在频谱分析中更常用。

频谱的相位

傅里叶变换的相位（即angle）通常用于研究信号通过滤波器等系统时频谱分量的时间延迟。在以下示例中，标准测试信号（单位功率的冲激信号）通过一个简单滤波器，该滤波器将输入延迟三个采样。输入包含\(n=50\)个采样，采样间隔\(T = 1\)秒。该图显示了输入和输出信号的幅度及相位随频率的变化。

import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np

from scipy import signal
from scipy.fft import rfft, rfftfreq

# Create input signal:
n = 50
x = np.zeros(n)
x[0] = n

# Apply FIR filter which delays signal by 3 samples:
y = signal.lfilter([0, 0, 0, 1], 1, x)

X, Y = (rfft(z_) / n for z_ in (x, y))
f = rfftfreq(n, 1)  # sampling interval T = 1 s

fig = plt.figure(tight_layout=True, figsize=(6., 4.))
gs = gridspec.GridSpec(3, 1)
ax0 = fig.add_subplot(gs[0, :])
ax1 = fig.add_subplot(gs[1:, :], sharex=ax0)

for Z_, n_, m_ in zip((X, Y), ("Input $X(f)$", "Output $Y(f)$"), ('+-', 'x-')):
    ax0.plot(f, abs(Z_), m_, alpha=.5, label=n_)
    ax1.plot(f, np.unwrap(np.angle(Z_)), m_, alpha=.5, label=n_)

ax0.set(title="Frequency Response of 3 Sample Delay Filter (no window)",
        ylabel="Magnitude", xlim=(0, f[-1]), ylim=(0, 1.1))
ax1.set(xlabel=rf"Frequency $f$ in Hertz ($\Delta f = {1/n}\,$Hz)",
        ylabel=r"Phase in rad")
ax1.set_yticks(-np.arange(0, 7)*np.pi/2,
               ['0', '-π/2', '-π', '-3/2π', '-2π', '-4/3π', '-3π'])

ax2 = ax1.twinx()
ax2.set(ylabel=r"Phase in Degrees", ylim=np.rad2deg(ax1.get_ylim()),
        yticks=np.arange(-540, 90, 90))
for ax_ in (ax0, ax1):
    ax_.legend()
    ax_.grid()
plt.show()

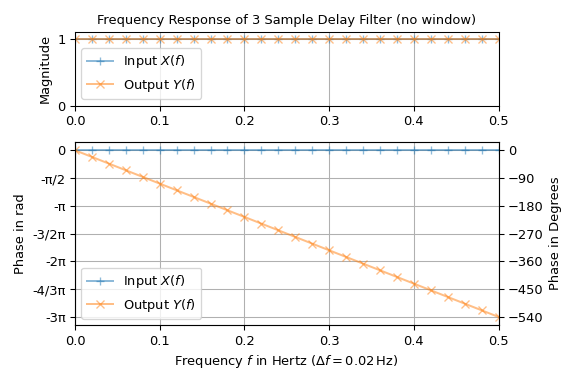
输入信号的傅里叶变换具有单位幅度和零相位，这就是其被用作测试信号的原因。输出信号也具有单位幅度，但相位线性下降，斜率为\(-6\pi\)。这是预期的，因为将信号\(x(t)\)延迟\(\Delta t\)会在其傅里叶变换中产生一个额外的线性相位项，即：

\[\int_\IR x(t-\Delta t) \e^{-\jj2\pi f t}\dd t = X(f)\, e^{-\jj2\pi \Delta t f}\ .\]

请注意，在图中，相位不限于区间\((+\pi, \pi]\)（angle的输出），因此没有任何不连续性。这是通过使用numpy.unwrap函数实现的。如果滤波器的传递函数已知，可以使用freqz直接确定滤波器的频谱响应。

平均频谱

periodogram函数计算功率谱密度（scaling='density'）或平方幅度谱（scaling='spectrum'）。为了获得平滑的周期图，可以使用welch函数。它通过将输入信号分成重叠的段来执行平滑，然后计算每个段的加窗DFT。结果是这些DFT的平均值。

下面的示例显示了一个信号的平方幅度谱和功率谱密度，该信号由一个频率为\(1.27\,\text{kHz}\)、幅度为\(\sqrt{2}\,\text{V}\)的正弦信号和具有平均谱功率密度为\(10^{-3}\,\text{V}^2/\text{Hz}\)的附加高斯噪声组成。

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal

rng = np.random.default_rng(73625)  # seeding for reproducibility

fs, n = 10e3, 10_000
f_x, noise_power = 1270, 1e-3 * fs / 2
t = np.arange(n) / fs
x = (np.sqrt(2) * np.sin(2 * np.pi * f_x * t) +
     rng.normal(scale=np.sqrt(noise_power), size=t.shape))

fg, axx = plt.subplots(1, 2, sharex='all', tight_layout=True, figsize=(7, 3.5))
axx[0].set(title="Squared Magnitude Spectrum", ylabel="Square of Magnitude in V²")
axx[1].set(title="Power Spectral Density", ylabel="Power Spectral Density in V²/Hz")
for ax_, s_ in zip(axx, ('spectrum', 'density')):
    f_p, P_p = signal.periodogram(x, fs, 'hann', scaling=s_)
    f_w, P_w = signal.welch(x, fs, scaling=s_)
    ax_.semilogy(f_p/1e3, P_p, label=f"Periodogram ({len(f_p)} bins)")
    ax_.semilogy(f_w/1e3, P_w, label=f"Welch's Method ({len(f_w)} bins)")
    ax_.set(xlabel="Frequency in kHz", xlim=(0, 2), ylim=(1e-7, 1.3))
    ax_.grid(True)
    ax_.legend(loc='lower center')
plt.show()

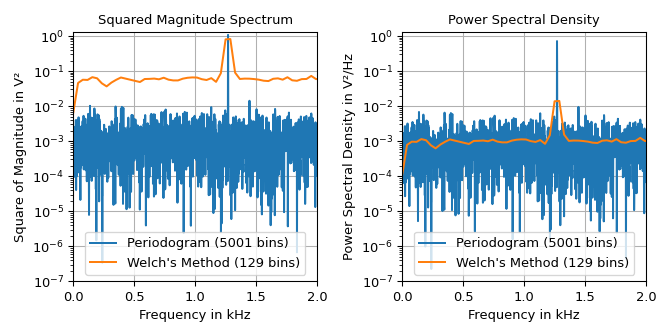
该图显示，welch函数以牺牲频率分辨率为代价，产生了更平滑的噪声基底。由于平滑，正弦信号的瓣高更宽，且不如周期图中的高。左图可用于读取瓣高，即正弦信号平方幅度的一半，为\(1\,\text{V}^2\)。右图可用于确定噪声基底为\(10^{-3}\,\text{V}^2/\text{Hz}\)。请注意，由于频率分辨率有限，平均平方幅度谱的瓣高不完全是1。可以通过零填充（例如，将nfft=4*len(x)传递给welch）或通过增加段长度（设置参数nperseg）来减少段数，从而增加频率分段的数量。

Lomb-Scargle 周期图（lombscargle）

最小二乘谱分析（LSSA）[6] [7]是一种估计频率谱的方法，它基于将正弦函数最小二乘拟合到数据样本，类似于傅里叶分析。傅里叶分析是科学中最常用的频谱方法，通常会在长时间间隔的记录中增强长周期噪声；LSSA则能减轻此类问题。

Lomb-Scargle 方法对非均匀采样数据执行频谱分析，并被认为是一种发现和测试弱周期信号显著性的有效方法。

对于包含\(N_{t}\)个测量值\(X_{j}\equiv X(t_{j})\)的时间序列，在时间\(t_{j}\)处采样（其中\((j = 1, \ldots, N_{t})\)），假设其已进行缩放和移位，使其平均值为零且方差为一，则在频率\(f\)处的归一化Lomb-Scargle周期图为

\[P_{n}(f) = \frac{1}{2}\left\{\frac{\left[\sum_{j}^{N_{t}}X_{j}\cos\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\cos^{2}\omega(t_{j}-\tau)}+\frac{\left[\sum_{j}^{N_{t}}X_{j}\sin\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\sin^{2}\omega(t_{j}-\tau)}\right\}.\]

此处，\(\omega \equiv 2\pi f\)是角频率。与频率相关的时间偏移\(\tau\)由下式给出

\[\tan 2\omega\tau = \frac{\sum_{j}^{N_{t}}\sin 2\omega t_{j}}{\sum_{j}^{N_{t}}\cos 2\omega t_{j}}.\]

lombscargle函数使用Zechmeister和Kürster[8]创建的稍作修改的算法计算周期图，该算法允许对单个样本进行加权并独立计算每个频率的未知偏移（也称为“浮动均值”）。

短时傅里叶变换

本节提供了使用ShortTimeFFT类的一些背景信息：短时傅里叶变换（STFT）可用于分析信号随时间的频谱特性。它通过使用滑动窗口将信号分成重叠的块，并计算每个块的傅里叶变换。对于连续时间复值信号\(x(t)\)，STFT的定义[9]如下：

\[S(f, t) := \int_\IR x(\xi)\, \conj{w(\xi-t)}\,\e^{-\jj2\pi f \xi}\dd\xi\ ,\]

其中\(w(t)\)是一个复值窗函数，其复共轭为\(\conj{w(t)}\)。它可以解释为确定\(x\)与窗函数\(w\)的标量积，其中窗函数\(w\)被时间\(t\)平移，然后被频率\(f\)调制（即频率偏移）。对于采样信号\(x[k] := x(kT)\)，\(k\in\IZ\)，采样间隔为\(T\)（即采样频率fs的倒数），需要使用离散版本，即仅在离散网格点\(S[q, p] := S(q \Delta f, p\Delta t)\)，\(q,p\in\IZ\)处评估STFT。它可以表示为

(8)\[S[q,p] = \sum_{k=0}^{N-1} x[k]\,\conj{w[k-p h]}\, \e^{-\jj2\pi q k / N}\ , \quad q,p\in\IZ\ ,\]

其中p表示\(S\)的时间索引，时间间隔为\(\Delta t := h T\)，\(h\in\IN\)（参见delta_t），这可以表示为\(h\)个样本的hop大小。\(q\)表示\(S\)的频率索引，步长为\(\Delta f := 1 / (N T)\)（参见delta_f），这使其与FFT兼容。\(w[m] := w(mT)\)，\(m\in\IZ\)是采样后的窗函数。

为了更贴合ShortTimeFFT的实现，将公式(8)重新表述为两步过程更有意义。

1. 通过长度为\(M\)（参见m_num）并以\(t[p] := p \Delta t = h T\)为中心（参见delta_t）的窗函数\(w[m]\)进行加窗，提取第\(p\)个切片，即：

   (9)\[x_p[m] = x\!\big[m - \lfloor M/2\rfloor + h p\big]\, \conj{w[m]}\ , \quad m = 0, \ldots M-1\ ,\]

   其中整数\(\lfloor M/2\rfloor\)表示M//2，即它是窗的中心点（m_num_mid）。为方便起见，假定\(x[k]:=0\)，当\(k\not\in\{0, 1, \ldots, N-1\}\)时。在滑动窗口小节中，将更详细地讨论切片的索引。

2. 然后对\(x_p[m]\)进行离散傅里叶变换（即FFT）。

   (10)\[S[q, p] = \sum_{m=0}^{M-1} x_p[m] \exp\!\big\{% -2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

   请注意，可以指定一个线性相位\(\phi_m\)（参见phase_shift），这对应于将输入移动\(\phi_m\)个采样。默认值为\(\phi_m = \lfloor M/2\rfloor\)（根据定义对应于phase_shift = 0），这会抑制未移位信号的线性相位分量。此外，FFT可以通过零填充\(w[m]\)进行过采样。这可以通过指定mfft大于窗长m_num来实现——这会将\(M\)设置为mfft（这意味着对于\(m\not\in\{0, 1, \ldots, M-1\}\)，\(w[m]:=0\)也成立）。

逆短时傅里叶变换（istft）通过反转这两个步骤来实现

1. 执行逆离散傅里叶变换，即：

   \[x_p[m] = \frac{1}{M}\sum_{q=0}^M S[q, p]\, \exp\!\big\{ 2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

2. 将通过\(w_d[m]\)加权的移位切片求和以重建原始信号，即：

   \[x[k] = \sum_p x_p\!\big[\mu_p(k)\big]\, w_d\!\big[\mu_p(k)\big]\ ,\quad \mu_p(k) = k + \lfloor M/2\rfloor - h p\]

   对于\(k \in [0, \ldots, n-1]\)。\(w_d[m]\)是\(w[m]\)的所谓对偶窗，也由\(M\)个样本组成。

请注意，对于所有窗函数和步长，逆STFT不一定存在。对于给定的窗函数\(w[m]\)，步长\(h\)必须足够小，以确保\(x[k]\)的每个样本都至少被一个非零窗片触及。这有时被称为“非零重叠条件”（参见check_NOLA）。更多详细信息将在逆STFT和对偶窗小节中给出。

滑动窗口

本小节通过一个示例讨论了ShortTimeFFT中滑动窗口的索引方式：考虑一个长度为6，hop间隔为2，采样间隔T为1的窗口，例如ShortTimeFFT(np.ones(6), 2, fs=1)。下图示意性地描绘了前四个窗口位置，也称为时间切片。

x轴表示时间\(t\)，对应于蓝色框底部行所示的样本索引k。y轴表示时间切片索引\(p\)。信号\(x[k]\)从索引\(k=0\)开始，并由浅蓝色背景标记。根据定义，第零个切片（\(p=0\)）以\(t=0\)为中心。每个切片的中心（m_num_mid），此处为样本6//2=3，由文本“mid”标记。默认情况下，stft计算所有与信号有重叠的切片。因此，第一个切片位于p_min = -1，最低样本索引为k_min = -5。第一个不受切片伸出信号左侧影响的样本索引是\(p_{lb} = 2\)，第一个不受边界效应影响的样本索引是\(k_{lb} = 5\)。属性lower_border_end返回元组\((k_{lb}, p_{lb})\)。

信号末端的行为如下所示，对于一个有\(n=50\)个样本的信号，由蓝色背景表示：

这里最后一个切片的索引是\(p=26\)。因此，根据Python的约定（结束索引不在范围内），p_max = 27表示第一个不接触信号的切片。对应的样本索引是k_max = 55。第一个伸出右侧的切片是\(p_{ub} = 24\)，其第一个样本位于\(k_{ub}=45\)。函数upper_border_begin返回元组\((k_{ub}, p_{ub})\)。

逆STFT和对偶窗

“对偶窗”一词源于帧理论[10]，其中帧是一种级数展开，可以表示给定希尔伯特空间中的任何函数。在此理论中，如果对于给定希尔伯特空间\(\mathcal{H}\)中的所有函数\(f\)，都满足以下条件，则展开式\(\{g_k\}\)和\(\{h_k\}\)是对偶帧：

\[f = \sum_{k\in\IN} \langle f, g_k\rangle h_k = \sum_{k\in\IN} \langle f, h_k\rangle g_k\ , \quad f \in \mathcal{H}\ ,\]

其中\(\langle ., .\rangle\)表示\(\mathcal{H}\)的标量积。所有帧都具有对偶帧[10]。

仅在离散网格点\(S(q \Delta f, p\Delta t)\)处评估的STFT在文献中被称为“Gabor帧”[9] [10]。由于窗函数\(w[m]\)的支持范围限于有限区间，ShortTimeFFT属于所谓的“无痛非正交展开”类别[9]。在这种情况下，对偶窗总是具有相同的支持范围，并且可以通过求对角矩阵的逆来计算。下面将粗略地推导，只需一些矩阵操作的理解即可。

由于公式(8)中给出的STFT是\(x[k]\)的线性映射，因此可以用向量-矩阵表示法表达。这使我们能够通过线性最小二乘法的形式解（如lstsq中）来表达逆，从而得到一个优美而简单的结果。

我们首先重新表述公式(9)的加窗操作。

(11)\[\begin{split} \vb{x}_p = \vb{W}_{\!p}\,\vb{x} = \begin{bmatrix} \cdots & 0 & w[0] & 0 & \cdots&&&\\ & \cdots & 0 & w[1] & 0 & \cdots&&\\ & & & & \ddots&&&\\ &&\cdots & 0 & 0 & w[M-1] & 0 & \cdots \end{bmatrix}\begin{bmatrix} x[0]\\ x[1]\\ \vdots\\ x[N-1] \end{bmatrix} ,\end{split}\]

其中\(M\times N\)矩阵\(\vb{W}_{\!p}\)仅在第\((ph)\)个次对角线上有非零项，即：

(12)\[\begin{split} W_p[m,k] = w[m]\, \delta_{m+ph,k}\ ,\quad \delta_{k,l} &= \begin{cases} 1 & \text{ for } k=l\ ,\\ 0 & \text{ elsewhere ,} \end{cases}\end{split}\]

其中\(\delta_{k,l}\)是克罗内克 delta。公式(10)可以表示为

(13)\[\vb{s}_p = \vb{F}\,\vb{x}_p \quad\text{with}\quad F[q,m] = \frac{1}{\sqrt{M}}\exp\!\big\{-2\jj\pi (q + \phi_m)\, m / M\big\}\ ,\]

这允许将第\(p\)个切片的STFT写为

(14)\[\vb{s}_p = \vb{F}\vb{W}_{\!p}\,\vb{x} =: \vb{G}_p\,\vb{x} \quad\text{with}\quad s_p[q] = S[p,q]\ .\]

由于缩放因子\(M^{-1/2}\)，\(\vb{F}\)是酉矩阵，即其逆等于其共轭转置，表示\(\conjT{\vb{F}}\vb{F} = \vb{I}\)。也允许其他缩放，例如公式(6)中的缩放，但在本节中会使符号稍微复杂。

为了获得STFT的单个向量-矩阵方程，将切片堆叠成一个向量，即：

\[\begin{split}\vb{s} := \begin{bmatrix} \vb{s}_0\\ \vb{s}_1\\ \vdots\\ \vb{s}_{P-1} \end{bmatrix} = \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix}\, \vb{x} =: \vb{G}\, \vb{x}\ ,\end{split}\]

其中\(P\)是结果STFT的列数。为了对该方程求逆，可以使用Moore-Penrose逆\(\vb{G}^\dagger\)：

(15)\[\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\, \conjT{\vb{G}} \vb{s} =: \vb{G}^\dagger \vb{s}\ ,\]

如果以下条件成立，则存在：

(16)\[\begin{split} \vb{D} := \conjT{\vb{G}}\vb{G} = \begin{bmatrix} \conjT{\vb{G}_0}& \conjT{\vb{G}_1}& \cdots & \conjT{\vb{G}_{P-1}} \end{bmatrix}^T \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p \ .\end{split}\]

是可逆的。那么\(\vb{x} = \vb{G}^\dagger\vb{G}\,\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\,\conjT{\vb{G}}\vb{G}\,\vb{x}\)显然成立。\(\vb{D}\)总是对角矩阵，其对角线元素非负。这在进一步简化\(\vb{D}\)后变得清晰：

(17)\[\vb{D} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p = \sum_{p=0}^{P-1} \conjT{(\vb{F}\,\vb{W}_{\!p})}\, \vb{F}\,\vb{W}_{\!p} = \sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\vb{W}_{\!p} =: \sum_{p=0}^{P-1} \vb{D}_p\]

由于\(\vb{F}\)是酉矩阵。此外

(18)\[\begin{split}D_p[r,s] &= \sum_{m=0}^{M-1} \conj{W_p^T[r,m]}\,W_p[m,s] = \sum_{m=0}^{M-1} \left(\conj{w[m]}\, \delta_{m+ph,r}\right) \left(w[m]\, \delta_{m+ph,s}\right)\\ &= \sum_{m=0}^{M-1} \big|w[m]\big|^2\, \delta_{r,s}\, \delta_{r,m+ph}\ .\end{split}\]

表明\(\vb{D}_p\)是一个对角矩阵，其元素非负。因此，对\(\vb{D}_p\)求和会保留该性质。这使得公式(15)能够进一步简化，即：

(19)\[\begin{split}\vb{x} &= \vb{D}^{-1} \conjT{\vb{G}}\vb{s} = \sum_{p=0}^{P-1} \vb{D}^{-1}\conjT{\vb{W}_{\!p}}\, \conjT{\vb{F}}\vb{s}_p = \sum_{p=0}^{P-1} (\conj{\vb{W}_{\!p}\vb{D}^{-1}})^T\, \conjT{\vb{F}}\vb{s}_p\\ &=: \sum_{p=0}^{P-1}\conjT{\vb{U}_p}\,\conjT{\vb{F}}\vb{s}_p\ .\end{split}\]

利用公式(12)、(17)、(18)，\(\vb{U}_p=\vb{W}_{\!p}\vb{D}^{-1}\)可以表示为

(20)\[\begin{split}U_p[m, k] &= W[m,k]\, D^{-1}[k,k] = \left(w[m] \delta_{m+ph,k}\right) \inv{\sum_{\eta=0}^{P-1} \vb{D}_\eta[k,k]} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1}\sum_{\mu=0}^{M-1} \big|w[\mu]\big|^2\,\delta_{m+ph, \mu+\eta h}} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1} \big|w[m+(p-\eta)h]\big|^2} \delta_{m+ph,k} \ .\end{split}\]

这表明\(\vb{U}_p\)与公式(12)中的\(\vb{W}_p\)具有相同的结构，即仅在第\((ph)\)个次对角线上有非零项。逆项中的求和可以解释为将\(|w[\mu]|^2\)滑动到\(w[m]\)上（并包含一个求逆操作），因此只有与\(w[m]\)重叠的分量才有效。因此，所有远离边界的\(U_p[m, k]\)都是相同的窗。为了避免边界效应，\(x[k]\)用零填充，从而扩大\(\vb{U}\)，使得所有接触\(x[k]\)的切片都包含相同的对偶窗。

(21)\[\begin{split} w_d[m] &= w[m] \inv{\sum_{\eta\in\IZ} \big|w[m + \eta\, h]\big|^2}\\ &=\ w[m] \inv{\sum_{l=0}^{M-1} \big|w[l]\big|^2 \delta_{l+m,\eta h}}\ , \quad \eta\in \IZ\ .\end{split}\]

由于当\(m \not\in\{0, \ldots, M-1\}\)时\(w[m] = 0\)成立，因此只需对满足\(|\eta| < M/h\)的索引\(\eta\)求和。第二个表达式是另一种形式，通过从索引\(l=0\)到\(M\)以\(h\)的增量求和。\(\delta_{l+m,\eta h}\)是克罗内克 delta 符号，表示(l+m) % h == 0。对偶窗这个名称可以通过将公式(14)插入公式(19)来证明，即：

(22)\[ \vb{x} = \sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\conjT{\vb{F}}\, \vb{F}\,\vb{W}_{\!p}\,\vb{x} = \left(\sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\vb{W}_{\!p}\right)\vb{x}\ ,\]

这表明\(\vb{U}_p\)和\(\vb{W}_{\!p}\)可以互换。由于\(\vb{U}_p\)和\(\vb{W}_{\!p}\)具有公式(11)中给出的相同结构，公式(22)包含所有可能的对偶窗的通用条件，即：

(23)\[\sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\,\vb{U}_p = \vb{I} \quad\Leftrightarrow\quad \sum_{p=0}^{P-1} \sum_{m=0}^{M-1} \conj{w[m]} u[m]\, \delta_{m+ph,i}\, \delta_{m+ph,j} = \delta_{i,j}\]

可以重新表述为

(24)\[\conjT{\vb{V}}\,\vb{u} = \vb{1}\ , \qquad V[i,j] := w[i]\, \delta_{i, j+ph}\ , \qquad \vb{V}\in \IC^{M\times h},\ p\in\IZ\ ,\]

其中\(\vb{1}\in\IR^h\)是一个全1向量。之所以\(\vb{V}\)只有\(h\)列，是因为公式(22)中第\(i\)行和第\((i+m)\)行（\(i\in\IN\)）是相同的。因此只有\(h\)个不同的方程。

实际应用中，寻找最接近给定向量\(\vb{d}\in\IC^M\)的有效对偶窗\(\vb{u}_d\)是一个兴趣点。通过利用\(h\)维的拉格朗日乘子向量\(\vb{\lambda}\)，我们得到凸二次规划问题：

\[\begin{split}\vb{u}_d = \min_{\vb{u}}{ \frac{1}{2}\lVert\vb{d} - \vb{u}\rVert^2 } \quad\text{w.r.t.}\quad \conjT{\vb{V}}\vb{u} = \vb{1} \qquad\Leftrightarrow\qquad \begin{bmatrix} \vb{I} & \vb{V}\\ \conjT{\vb{V}} & \vb{0} \end{bmatrix} \begin{bmatrix} \vb{u}_d \\ \vb{\lambda} \end{bmatrix} = \begin{bmatrix} \vb{d}\\ \vb{1} \end{bmatrix}\ .\end{split}\]

通过对\(2\times2\)块矩阵进行符号求逆，可以计算出一个封闭形式的解，得到

(25)\[\begin{split}\vb{u}_d &= \underbrace{\vb{V}\inv{\conjT{\vb{V}}\vb{V}}}_{% =:\vb{Q}\in\IC^{M\times h}} \vb{1} + \big(\vb{I} - \vb{Q}\conjT{\vb{V}}\big)\vb{d} = \vb{w}_d + \vb{d} - \vb{q}_d\ ,\\ \vb{w}_d &= \vb{Q}\vb{1}\ ,\qquad \vb{q}_d = \vb{Q}\conjT{\vb{V}}\vb{d}\ ,\\ Q[i,j] &= \frac{ w[i] \delta_{i-j, \eta h} }{% \sum_{k=0}^M |w[k]|^2\,\delta_{i-k, \xi h} } ,\qquad w_d[i] = \frac{w[i] }{ \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \xi h} }\ ,\\ q_d[i] &= w[i] \frac{\sum_{j=1}^h \delta_{i-j, \eta h} \sum_{l=1}^M \conj{w[l]} d[l] \delta_{j-l, \xi h} }{% \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \zeta h} } = w_d[i] \sum_{l=1}^M \conj{w[l]} d[l] \delta_{i-l, \eta h}\ ,\end{split}\]

其中\(\eta,\xi,\zeta\in\IZ\)。请注意，第一个项\(\vb{w}_d\)等于公式(21)中给出的解，并且\(\conjT{\vb{V}}\vb{V}\)的逆必须存在，否则STFT不可逆。当\(\vb{d}=\vb{0}\)时，得到解\(\vb{w}_d\)。因此，\(\vb{w}_d\)最小化\(L^2\)范数\(\lVert\vb{u}\rVert\)，这是其名称“规范对偶窗”的理由。有时，更希望找到方向上最接近且忽略向量长度的向量。这可以通过引入比例因子\(\alpha\in\IC\)来最小化\(\lVert\alpha\vb{d} - \vb{u}\rVert^2\)来实现。由于公式(25)已经提供了通用解，我们可以写成：

\[\begin{split} \alpha_{\min} &= \min_{\alpha}{ \frac{1}{2}\big\lVert\alpha\vb{d} - \vb{u}_d(\alpha)\big\rVert^2 }\ ,\qquad \vb{u}_d(\alpha) = \vb{w}_d + \alpha\vb{d} - \alpha\vb{q}_d \qquad\Leftrightarrow\\ \alpha_{\min} &= \conjT{\vb{q}_d}\vb{w}_d \big/\, \conjT{\vb{q}_d}\vb{q}_d \ .\end{split}\]

当窗函数\(w[m]\)和对偶窗\(u[m]\)相等时的情况，可以很容易地从公式(23)推导出来，结果是\(h\)个形式为以下条件的方程：

(26)\[\sum_{p=0}^{\lfloor M / h \rfloor} \big|w[m+ph]\big|^2 = 1\ , \qquad m \in \{0, \ldots, h-1\}\ .\]

请注意，每个窗口样本\(w[m]\)在\(h\)个方程中只出现一次。对于给定窗口\(\vb{d}\)，找到最接近的窗口\(\vb{w}\)是直接的：根据公式(26)划分\(\vb{d}\)，并将每个部分的长度归一化为1。在这种情况下，\(w[m]\)也是一个规范对偶窗口，这可以通过在公式(24)中设置\(u[m]=w[m]\)，这等效于公式(21)中的分母为1来证明。

此外，如果公式(26)成立，则公式(16)的矩阵\(\vb{D}\)是单位矩阵，使得STFT \(\vb{G}\)是一个酉映射，即\(\conjT{\vb{G}}\vb{G}=\vb{I}\)。请注意，这仅在公式(13)中使用了酉DFT时才成立。ShortTimeFFT的实现使用了公式(6)的标准DFT。因此，STFT空间中的标量积需要缩放\(1/M\)以确保酉映射的关键性质——标量积相等——成立。即：

(27)\[\langle x, y\rangle = \sum_k x[k]\, \conj{y[k]} \stackrel{\stackrel{\text{unitary}}{\downarrow}}{=} \frac{1}{M}\sum_{q,p} S_x[q,p]\, \conj{S_y[q,p]}\ ,\]

其中\(S_{x,y}\)是\(x,y\)的STFT。或者，可以将窗函数按\(1/\sqrt{M}\)缩放，对偶窗按\(\sqrt{M}\)缩放以获得酉映射，这在from_win_equals_dual中实现。

与旧有实现的比较

函数stft、istft和spectrogram早于ShortTimeFFT实现。本节讨论旧的“旧有”（legacy）实现和新的ShortTimeFFT实现之间的主要区别。重写的核心动机是认识到，在不破坏兼容性的情况下，无法以合理的方式集成对偶窗。这为重新思考代码结构和参数化提供了机会，从而使一些隐式行为变得更加显式。

以下示例比较了一个负斜率复值chirp信号的两种STFT：

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import fftshift
>>> from scipy.signal import stft, istft, spectrogram, ShortTimeFFT
...
>>> fs, N = 200, 1001  # 200 Hz sampling rate for 5 s signal
>>> t_z = np.arange(N) / fs  # time indexes for signal
>>> z = np.exp(2j*np.pi*70 * (t_z - 0.2*t_z**2))  # complex-valued chirp
...
>>> nperseg, noverlap = 50, 40
>>> win = ('gaussian', 1e-2 * fs)  # Gaussian with 0.01 s standard dev.
...
>>> # Legacy STFT:
>>> f0_u, t0, Sz0_u = stft(z, fs, win, nperseg, noverlap,
...                        return_onesided=False, scaling='spectrum')
>>> f0, Sz0 = fftshift(f0_u), fftshift(Sz0_u, axes=0)
...
>>> # New STFT:
>>> SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap, fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz1 = SFT.stft(z)
...
>>> # Plot results:
>>> fig1, axx = plt.subplots(2, 1, sharex='all', sharey='all',
...                          figsize=(6., 5.))  # enlarge figure a bit
>>> t_lo, t_hi, f_lo, f_hi = SFT.extent(N, center_bins=True)
>>> axx[0].set_title(r"Legacy stft() produces $%d\times%d$ points" % Sz0.T.shape)
>>> axx[0].set_xlim(t_lo, t_hi)
>>> axx[0].set_ylim(f_lo, f_hi)
>>> axx[1].set_title(r"ShortTimeFFT produces $%d\times%d$ points" % Sz1.T.shape)
>>> axx[1].set_xlabel(rf"Time $t$ in seconds ($\Delta t= {SFT.delta_t:g}\,$s)")
...
>>> # Calculate extent of plot with centered bins since
>>> # imshow does not interpolate by default:
>>> dt2 = (nperseg-noverlap) / fs / 2  # equals SFT.delta_t / 2
>>> df2 = fs / nperseg / 2  # equals SFT.delta_f / 2
>>> extent0 = (-dt2, t0[-1] + dt2, f0[0] - df2, f0[-1] - df2)
>>> extent1 = SFT.extent(N, center_bins=True)
...
>>> kw = dict(origin='lower', aspect='auto', cmap='viridis')
>>> im1a = axx[0].imshow(abs(Sz0), extent=extent0, **kw)
>>> im1b = axx[1].imshow(abs(Sz1), extent=extent1, **kw)
>>> fig1.colorbar(im1b, ax=axx, label="Magnitude $|S_z(t, f)|$")
>>> _ = fig1.supylabel(r"Frequency $f$ in Hertz ($\Delta f = %g\,$Hz)" %
...                    SFT.delta_f, x=0.08, y=0.5, fontsize='medium')
>>> plt.show()

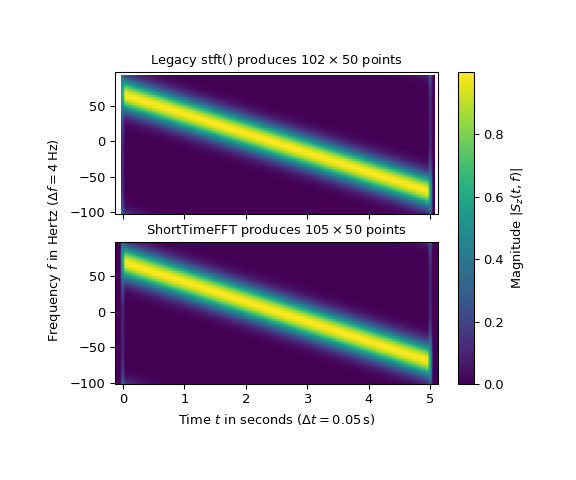
ShortTimeFFT比旧有版本多生成3个时间切片是主要区别。如滑动窗口一节所述，所有接触信号的切片都包含在新版本中。这样做的好处是STFT可以像ShortTimeFFT代码示例中所示的那样进行切片和重组。此外，使用所有接触切片使得ISTFT在某些窗函数为零的情况下更鲁棒。

请注意，具有相同时间戳的切片会产生相同的结果（在数值精度范围内），即

>>> np.allclose(Sz0, Sz1[:, 2:-1])
True

通常，这些额外的切片包含非零值。由于我们示例中的大量重叠，它们相当小。例如，

>>> abs(Sz1[:, 1]).min(), abs(Sz1[:, 1]).max()
(6.925060911593139e-07, 8.00271269218721e-07)

ISTFT可用于重建原始信号

>>> t0_r, z0_r = istft(Sz0_u, fs, win, nperseg, noverlap,
...                    input_onesided=False, scaling='spectrum')
>>> z1_r = SFT.istft(Sz1, k1=N)
...
>>> len(z0_r), len(z)
(1010, 1001)
>>> np.allclose(z0_r[:N], z)
True
>>> np.allclose(z1_r, z)
True

请注意，旧版实现返回的信号比原始信号长。另一方面，新的istft允许明确指定重建信号的起始索引k0和结束索引k1。旧实现中的长度差异是由于信号长度不是切片长度的倍数造成的。

本例中新旧版本之间的其他差异包括：

• 参数fft_mode='centered'确保在绘图时，对于双边FFT，零频率垂直居中。对于旧版实现，需要使用fftshift。fft_mode='twosided'产生与旧版相同的行为。

• 参数phase_shift=None确保两个版本具有相同的相位。ShortTimeFFT的默认值0会产生具有额外线性相位项的STFT切片。

语谱图被定义为STFT的绝对平方[9]。ShortTimeFFT提供的spectrogram遵循该定义，即：

>>> np.allclose(SFT.spectrogram(z), abs(Sz1)**2)
True

另一方面，旧版的spectrogram提供了另一种STFT实现，其主要区别在于对信号边界的不同处理。以下示例展示了如何使用ShortTimeFFT获得与旧版spectrogram产生的SFT相同的结果：

>>> # Legacy spectrogram (detrending for complex signals not useful):
>>> f2_u, t2, Sz2_u = spectrogram(z, fs, win, nperseg, noverlap,
...                               detrend=None, return_onesided=False,
...                               scaling='spectrum', mode='complex')
>>> f2, Sz2 = fftshift(f2_u), fftshift(Sz2_u, axes=0)
...
>>> # New STFT:
... SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap,
...                                fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz3 = SFT.stft(z, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
>>> t3 = SFT.t(N, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
...
>>> np.allclose(t2, t3)
True
>>> np.allclose(f2, SFT.f)
True
>>> np.allclose(Sz2, Sz3)
True

与其他STFT的区别在于，时间切片不是从0开始，而是从nperseg//2开始，即：

>>> t2
array([0.125, 0.175, 0.225, 0.275, 0.325, 0.375, 0.425, 0.475, 0.525,
       ...
       4.625, 4.675, 4.725, 4.775, 4.825, 4.875])

此外，只返回不向右突出的切片，最后一个切片以4.875秒为中心，这使其比默认的stft参数化更短。

使用mode参数，旧版spectrogram还可以返回“角度”、“相位”、“PSD”或“幅度”。旧版spectrogram的scaling行为不直接，因为它取决于参数mode、scaling和return_onesided。ShortTimeFFT中并非所有组合都有直接对应关系，因为它只提供“幅度”、“PSD”或根本不进行窗函数scaling。下表显示了这些对应关系：

旧版spectrogram				ShortTimeFFT
模式（mode）	缩放（scaling）	返回单边（return_onesided）		fft_模式（fft_mode）	缩放（scaling）
功率谱密度（psd）	密度（density）	真（True）		单边2X（onesided2X）	功率谱密度（psd）
功率谱密度（psd）	密度（density）	假（False）		双边（twosided）	功率谱密度（psd）
幅度（magnitude）	频谱（spectrum）	真（True）		单边（onesided）	幅度（magnitude）
幅度（magnitude）	频谱（spectrum）	假（False）		双边（twosided）	幅度（magnitude）
复数（complex）	频谱（spectrum）	真（True）		单边（onesided）	幅度（magnitude）
复数（complex）	频谱（spectrum）	假（False）		双边（twosided）	幅度（magnitude）
功率谱密度（psd）	频谱（spectrum）	真（True）		—	—
功率谱密度（psd）	频谱（spectrum）	假（False）		—	—
复数（complex）	密度（density）	真（True）		—	—
复数（complex）	密度（density）	假（False）		—	—
幅度（magnitude）	密度（density）	真（True）		—	—
幅度（magnitude）	密度（density）	假（False）		—	—
—	—	—		*	无（None）

当对复值输入信号使用onesided输出时，旧版spectrogram会切换到two-sided模式。ShortTimeFFT会引发TypeError，因为所使用的rfft函数只接受实值输入。关于由各种参数化引起的各种频谱表示的讨论，请参阅上面的频谱分析部分。

参考文献

更多阅读和相关软件

[1]

“傅里叶变换”，维基百科，https://en.wikipedia.org/wiki/Fourier_transform

[2]

“频谱密度”，维基百科，https://en.wikipedia.org/wiki/Spectral_density

[3]

“离散傅里叶变换”，维基百科，https://en.wikipedia.org/wiki/Discrete_Fourier_transform

[4]

“频谱泄漏”，维基百科，https://en.wikipedia.org/wiki/Spectral_leakage

[5]

“奈奎斯特–香农采样定理”，维基百科，https://en.wikipedia.org/wiki/Nyquist-Shannon_sampling_theorem

[6]

N.R. Lomb “不等间隔数据的最小二乘频率分析”，Astrophysics and Space Science, vol 39, pp. 447-462, 1976

[7]

J.D. Scargle “天文时间序列分析研究。II - 不等间隔数据频谱分析的统计方面”，The Astrophysical Journal, vol 263, pp. 835-853, 1982

[8]

M. Zechmeister 和 M. Kürster，《广义Lomb-Scargle周期图。浮动均值和开普勒周期图的新形式》，Astronomy and Astrophysics, vol. 496, pp. 577-584, 2009

[9] (1,2,3,4)

Karlheinz Gröchenig：《时频分析基础》，Birkhäuser Boston 2001，DOI:10.1007/978-1-4612-0003-1

[10] (1,2,3)

Ole Christensen：《帧和里斯基底导论》，Birkhäuser Boston 2016，DOI:10.1007/978-3-319-25613-9