scipy.signal.

fftconvolve

scipy.signal.fftconvolve(in1, in2, mode='full', axes=None)

使用 FFT 卷积两个 N 维数组。

使用快速傅里叶变换方法卷积 in1 和 in2，输出大小由 mode 参数确定。

对于大型数组 (n > ~500)，这通常比 convolve 快得多，但当只需要少量输出值时可能会较慢，并且只能输出浮点数组（整数或对象数组输入将转换为浮点数）。

从 v0.19 开始，convolve 会根据对哪个更快做出估计，自动选择此方法或直接方法。

参数:

in1array_like

第一个输入。

in2array_like

第二个输入。应具有与 in1 相同的维度数。

modestr {‘full’, ‘valid’, ‘same’}, 可选

一个字符串，指示输出的大小

full

输出是输入的完整离散线性卷积。（默认）

valid

输出仅包含那些不依赖于零填充的元素。在“valid”模式下，in1 或 in2 在每个维度上都必须至少与另一个一样大。

same

输出的大小与 in1 相同，相对于“full”输出居中。

axesint 或 int 数组或 None，可选

计算卷积的轴。默认值是对所有轴进行计算。

返回:

out数组

一个 N 维数组，包含 in1 与 in2 的离散线性卷积的子集。

另请参阅

convolve

根据哪个更快使用直接卷积或 FFT 卷积算法。

oaconvolve

使用重叠相加法进行卷积，当输入数组很大且大小差异很大时，通常速度更快。

示例

在您的浏览器中尝试！

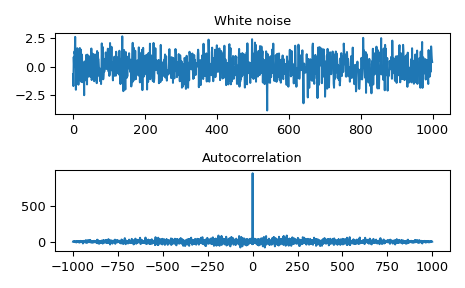
白噪声的自相关是一个脉冲。

>>> import numpy as np
>>> from scipy import signal
>>> rng = np.random.default_rng()
>>> sig = rng.standard_normal(1000)
>>> autocorr = signal.fftconvolve(sig, sig[::-1], mode='full')

>>> import matplotlib.pyplot as plt
>>> fig, (ax_orig, ax_mag) = plt.subplots(2, 1)
>>> ax_orig.plot(sig)
>>> ax_orig.set_title('White noise')
>>> ax_mag.plot(np.arange(-len(sig)+1,len(sig)), autocorr)
>>> ax_mag.set_title('Autocorrelation')
>>> fig.tight_layout()
>>> fig.show()

使用 FFT 卷积实现的 Gaussian 模糊。 请注意图像周围的黑色边框，这是由于超出其边界的零填充造成的。 convolve2d 函数允许其他类型的图像边界，但速度慢得多。

>>> from scipy import datasets
>>> face = datasets.face(gray=True)
>>> kernel = np.outer(signal.windows.gaussian(70, 8),
...                   signal.windows.gaussian(70, 8))
>>> blurred = signal.fftconvolve(face, kernel, mode='same')

>>> fig, (ax_orig, ax_kernel, ax_blurred) = plt.subplots(3, 1,
...                                                      figsize=(6, 15))
>>> ax_orig.imshow(face, cmap='gray')
>>> ax_orig.set_title('Original')
>>> ax_orig.set_axis_off()
>>> ax_kernel.imshow(kernel, cmap='gray')
>>> ax_kernel.set_title('Gaussian kernel')
>>> ax_kernel.set_axis_off()
>>> ax_blurred.imshow(blurred, cmap='gray')
>>> ax_blurred.set_title('Blurred')
>>> ax_blurred.set_axis_off()
>>> fig.show()

返回在新标签页中打开