scipy.signal.

lombscargle#

scipy.signal.lombscargle(x, y, freqs, precenter=False, normalize=False, *, weights=None, floating_mean=False)[source]#

计算广义 Lomb-Scargle 周期图。

Lomb-Scargle 周期图由 Lomb [1] 开发，并由 Scargle [2] 进一步扩展，用于寻找并检验具有不均匀时间采样的弱周期信号的显著性。这里使用的算法基于以下形式的加权最小二乘拟合：y(ω) = a*cos(ω*x) + b*sin(ω*x) + c，其中拟合是针对每个频率独立计算的。该算法由 Zechmeister 和 Kürster 开发，通过允许对单个样本进行加权并计算未知的 y 偏移（也称为“浮动平均”模型）来改进 Lomb-Scargle 周期图 [3]。有关更多详细信息和实际考虑因素，请参阅关于 Lomb-Scargle 周期图的优秀参考资料 [4]。

当 normalize 为 False（或“power”）（默认）时，计算出的周期图未经归一化，对于幅度为 A 的谐波信号，当 N 足够大时，它取值 (A**2) * N/4。其中 N 是 x 或 y 的长度。

当 normalize 为 True（或“normalize”）时，计算出的周期图通过数据围绕恒定参考模型（在零点）的残差进行归一化。

当 normalize 为“amplitude”时，计算出的周期图是幅度和相位的复数表示。

输入数组应为真实浮点数据类型的 1 维数组，它们在处理前会转换为 float64 数组。

参数:

x数组类型: 采样时间。
y数组类型: 测量值。假设值为基线 y = 0。如果可能存在 y 偏移，建议将 floating_mean 设置为 True。
freqs数组类型: 角频率（例如，当 x 单位为 s 时，其单位为 rad/s=2π/s）用于输出周期图。频率通常 >= 0，因为在 -freq 处的任何峰值也将在 +freq 处存在。
precenter布尔型，可选: 如果为 True，则通过减去均值来预居中测量值。这是一个遗留参数，如果 floating_mean 为 True，则无需设置此参数。
normalize布尔型 | 字符串型，可选: 计算归一化或复数（幅度 + 相位）周期图。有效选项包括：False/"power"、True/"normalize" 或 "amplitude"。
weights数组类型，可选: 每个样本的权重。权重必须是非负的。
floating_mean布尔型，可选: 如果为 True，则独立地为每个频率确定一个 y 偏移。否则，y 偏移假定为 0。

返回值:

pgram数组类型: Lomb-Scargle 周期图。

抛出:

ValueError: 如果输入数组 x、y、freqs 或 weights 中的任何一个不是 1 维，或者任何一个长度为零。或者，如果输入数组 x、y 和 weights 的形状彼此不相同。
ValueError: 如果任何权重 < 0，或者权重之和 <= 0。
ValueError: 如果 normalize 参数不是允许的选项之一。

另请参见

periodogram: 使用周期图的功率谱密度
welch: 使用 Welch 方法的功率谱密度
csd: 使用 Welch 方法的交叉谱密度

注释

除非 floating_mean 为 True，否则所使用的算法不会自动处理任何未知的 y 偏移。因此，在大多数使用情况下，如果存在 y 偏移的可能性，建议将 floating_mean 设置为 True。如果 precenter 为 True，它将执行操作 y -= y.mean()。然而，precenter 是一个遗留参数，当 floating_mean 为 True 时，它是不必要的。此外，通过 precenter 移除的均值不考虑样本权重，也不会纠正由于在峰值和/或谷值处持续缺失观测而导致的任何偏差。当 normalize 参数为“amplitude”时，对于 freqs 中低于 (2*pi)/(x.max() - x.min()) 的任何频率，预测的幅度将趋于无穷大。“奈奎斯特频率”限制的概念（参见奈奎斯特-香农采样定理）通常不适用于不均匀采样的数据。因此，对于不均匀采样的数据，freqs 中的有效频率通常会比预期高得多。

参考文献

[1]

N.R. Lomb “不等间距数据的最小二乘频率分析”, Astrophysics and Space Science, vol 39, pp. 447-462, 1976 DOI:10.1007/bf00648343

[2]

J.D. Scargle “天文学时间序列分析研究。二 - 不等间距数据谱分析的统计方面”, The Astrophysical Journal, vol 263, pp. 835-853, 1982 DOI:10.1086/160554

[3]

M. Zechmeister and M. Kürster, “广义 Lomb-Scargle 周期图。一种用于浮动平均和开普勒周期图的新形式,” Astronomy and Astrophysics, vol. 496, pp. 577-584, 2009 DOI:10.1051/0004-6361:200811296

[4]

J.T. VanderPlas, “理解 Lomb-Scargle 周期图,” The Astrophysical Journal Supplement Series, vol. 236, no. 1, p. 16, May 2018 DOI:10.3847/1538-4365/aab766

示例

>>> import numpy as np
>>> rng = np.random.default_rng()

首先定义信号的一些输入参数

>>> A = 2.  # amplitude
>>> c = 2.  # offset
>>> w0 = 1.  # rad/sec
>>> nin = 150
>>> nout = 1002

随机生成采样时间

>>> x = rng.uniform(0, 10*np.pi, nin)

绘制选定时间的正弦波

>>> y = A * np.cos(w0*x) + c

定义用于计算周期图的频率数组

>>> w = np.linspace(0.25, 10, nout)

计算每种归一化选项的 Lomb-Scargle 周期图

>>> from scipy.signal import lombscargle
>>> pgram_power = lombscargle(x, y, w, normalize=False)
>>> pgram_norm = lombscargle(x, y, w, normalize=True)
>>> pgram_amp = lombscargle(x, y, w, normalize='amplitude')
...
>>> pgram_power_f = lombscargle(x, y, w, normalize=False, floating_mean=True)
>>> pgram_norm_f = lombscargle(x, y, w, normalize=True, floating_mean=True)
>>> pgram_amp_f = lombscargle(x, y, w, normalize='amplitude', floating_mean=True)

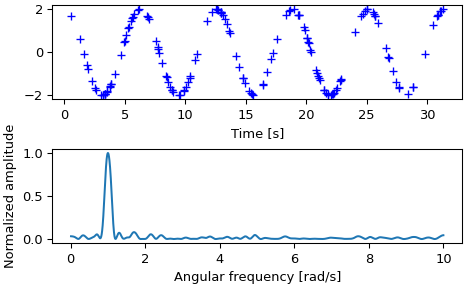
现在绘制输入数据

>>> import matplotlib.pyplot as plt
>>> fig, (ax_t, ax_p, ax_n, ax_a) = plt.subplots(4, 1, figsize=(5, 6))
>>> ax_t.plot(x, y, 'b+')
>>> ax_t.set_xlabel('Time [s]')
>>> ax_t.set_ylabel('Amplitude')

然后绘制每种归一化选项的周期图，包括 floating_mean=True 和 floating_mean=False 的情况

>>> ax_p.plot(w, pgram_power, label='default')
>>> ax_p.plot(w, pgram_power_f, label='floating_mean=True')
>>> ax_p.set_xlabel('Angular frequency [rad/s]')
>>> ax_p.set_ylabel('Power')
>>> ax_p.legend(prop={'size': 7})
...
>>> ax_n.plot(w, pgram_norm, label='default')
>>> ax_n.plot(w, pgram_norm_f, label='floating_mean=True')
>>> ax_n.set_xlabel('Angular frequency [rad/s]')
>>> ax_n.set_ylabel('Normalized')
>>> ax_n.legend(prop={'size': 7})
...
>>> ax_a.plot(w, np.abs(pgram_amp), label='default')
>>> ax_a.plot(w, np.abs(pgram_amp_f), label='floating_mean=True')
>>> ax_a.set_xlabel('Angular frequency [rad/s]')
>>> ax_a.set_ylabel('Amplitude')
>>> ax_a.legend(prop={'size': 7})
...
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-lombscargle-1.png