scipy.signal.

periodogram#

scipy.signal.periodogram(x, fs=1.0, window='boxcar', nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1)[source]#

使用周期图估计功率谱密度。

参数:
xarray_like

测量值的时间序列。

fsfloat, optional

x 时间序列的采样频率。默认为 1.0。

windowstr or tuple or array_like, optional

要使用的期望窗口。如果 window 是字符串或元组，它将传递给 get_window 以生成窗口值，默认情况下这些值是 DFT 偶对称的。有关窗口列表和所需参数，请参阅 get_window。如果 window 是 array_like，它将直接用作窗口，其长度必须等于计算周期图的轴的长度。默认为 'boxcar'。

nfftint, optional

所用 FFT 的长度。如果为 None，则将使用 x 的长度。

detrendstr or function or False, optional

指定如何对每个段进行去趋势。如果 detrend 是一个字符串，它将作为 type 参数传递给 detrend 函数。如果它是一个函数，它接受一个段并返回一个去趋势的段。如果 detrend 为 False，则不进行去趋势。默认为 'constant'。

return_onesidedbool, optional

如果为 True，则返回实数数据的一侧频谱。如果为 False，则返回双侧频谱。默认为 True，但对于复数数据，始终返回双侧频谱。

scaling{ ‘density’, ‘spectrum’ }, optional

选择计算功率谱密度 ('density') 或平方幅度谱 ('spectrum')。如果 x 以 V 为单位测量，fs 以 Hz 为单位测量，则在 'density' 模式下 Pxx 的单位为 V²/Hz，在 'spectrum' 模式下 Pxx 的单位为 V²。默认为 'density'。

axisint, optional

计算周期图的轴；默认为最后一个轴（即 axis=-1）。

返回:
fndarray

采样频率数组。

Pxxndarray

x 的功率谱密度或功率谱。

另请参阅

welch

使用 Welch 方法估计功率谱密度

lombscargle

非均匀采样数据的 Lomb-Scargle 周期图

备注

平方幅度（scaling='spectrum'）除以谱功率密度（scaling='density'）的比值是常数因子 sum(abs(window)**2)*fs / abs(sum(window))**2。如果 return_onesided 为 True，则负频率的值会添加到相应的正频率值中。

有关功率谱密度和幅度（平方）谱的标定，请查阅 谱分析 部分的 SciPy 用户指南。

0.12.0 版中新增。

示例

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

生成一个测试信号，一个 1234 Hz 的 2 Vrms 正弦波，受 0.001 V**2/Hz 白噪声干扰，以 10 kHz 采样。

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2*np.sqrt(2)
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> x = amp*np.sin(2*np.pi*freq*time)
>>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)

计算并绘制功率谱密度。

>>> f, Pxx_den = signal.periodogram(x, fs)
>>> plt.semilogy(f, Pxx_den)
>>> plt.ylim([1e-7, 1e2])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('PSD [V**2/Hz]')
>>> plt.show()
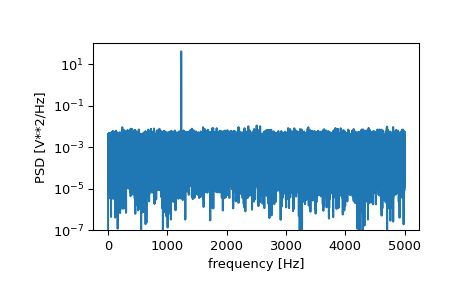
../../_images/scipy-signal-periodogram-1_00_00.png

如果我们对功率谱密度的后半部分进行平均，以排除峰值，我们可以恢复信号上的噪声功率。

>>> np.mean(Pxx_den[25000:])
0.000985320699252543

现在计算并绘制功率谱。

>>> f, Pxx_spec = signal.periodogram(x, fs, 'flattop', scaling='spectrum')
>>> plt.figure()
>>> plt.semilogy(f, np.sqrt(Pxx_spec))
>>> plt.ylim([1e-4, 1e1])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Linear spectrum [V RMS]')
>>> plt.show()
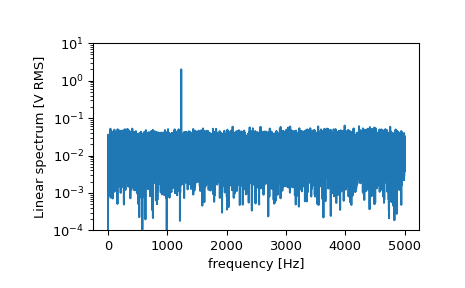
../../_images/scipy-signal-periodogram-1_01_00.png

功率谱中的峰值高度是 RMS 振幅的估计值。

>>> np.sqrt(Pxx_spec.max())
2.0077340678640727
本页内容