scipy.signal.

detrend#

scipy.signal.detrend(data, axis=-1, type='linear', bp=0, overwrite_data=False)[source]#

沿轴从数据中移除线性或常量趋势。

参数:

dataarray_like: 输入数据。
axisint, optional: 对数据进行去趋势处理的轴。默认值为最后一个轴 (-1)。
type{‘linear’, ‘constant’}, optional: 去趋势的类型。如果 type == 'linear' (默认)，则从 data 中减去对 data 进行线性最小二乘拟合的结果。如果 type == 'constant'，则只减去 data 的均值。
bparray_like of ints, optional: 一系列断点。如果给定，则对两个断点之间 data 的每个部分执行单独的线性拟合。断点指定为 data 中的索引。此参数仅在 type == 'linear' 时有效。
overwrite_databool, optional: 如果为 True，则执行原地去趋势处理并避免复制。默认为 False

返回:

retndarray: 去趋势后的输入数据。

另请参阅

numpy.polynomial.polynomial.Polynomial.fit: 创建最小二乘拟合多项式。

说明

去趋势可以解释为减去最小二乘拟合多项式：将参数 type 设置为“constant”对应于拟合零次多项式，“linear”对应于拟合一次多项式。请参阅下面的示例。

示例

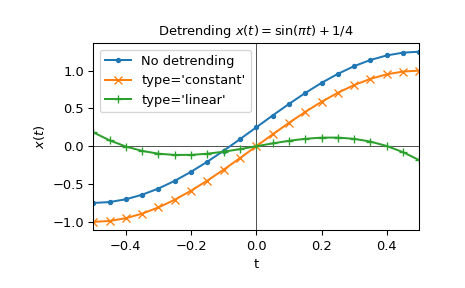
以下示例对函数 \(x(t) = \sin(\pi t) + 1/4\) 进行去趋势处理

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import detrend
...
>>> t = np.linspace(-0.5, 0.5, 21)
>>> x = np.sin(np.pi*t) + 1/4
...
>>> x_d_const = detrend(x, type='constant')
>>> x_d_linear = detrend(x, type='linear')
...
>>> fig1, ax1 = plt.subplots()
>>> ax1.set_title(r"Detrending $x(t)=\sin(\pi t) + 1/4$")
>>> ax1.set(xlabel="t", ylabel="$x(t)$", xlim=(t[0], t[-1]))
>>> ax1.axhline(y=0, color='black', linewidth=.5)
>>> ax1.axvline(x=0, color='black', linewidth=.5)
>>> ax1.plot(t, x, 'C0.-',  label="No detrending")
>>> ax1.plot(t, x_d_const, 'C1x-', label="type='constant'")
>>> ax1.plot(t, x_d_linear, 'C2+-', label="type='linear'")
>>> ax1.legend()
>>> plt.show()

../../_images/scipy-signal-detrend-1_00_00.png

或者，NumPy 的 Polynomial 也可以用于去趋势处理

>>> pp0 = np.polynomial.Polynomial.fit(t, x, deg=0)  # fit degree 0 polynomial
>>> np.allclose(x_d_const, x - pp0(t))  # compare with constant detrend
True
>>> pp1 = np.polynomial.Polynomial.fit(t, x, deg=1)  # fit degree 1 polynomial
>>> np.allclose(x_d_linear, x - pp1(t))  # compare with linear detrend
True

请注意，Polynomial 也允许拟合更高次的多项式。请参阅其文档以了解如何提取多项式系数。