resample#
- scipy.signal.resample(x, num, t=None, axis=0, window=None, domain='time')[source]#
使用傅里叶方法,沿着给定axis,将x重采样为num个样本。
通过对x的FFT进行截断或零填充来执行重采样。这样做的好处是提供了一个理想的抗混叠滤波器,并允许任意的升采样或降采样比率。主要缺点是需要假定x是周期信号。
- 参数:
- x类数组
由等距样本组成的输入信号。如果x是多维数组,参数axis指定时间/频率轴。这里假设
n_x = x.shape[axis]指定样本数量,T指定采样间隔。- num整型
重采样输出信号的样本数量。它可以大于或小于
n_x。- t类数组, 可选
如果t不是
None,则也会返回重采样信号的时间戳。t必须包含输入信号x的至少前两个时间戳(所有其他时间戳将被忽略)。输出信号的时间戳由t[0] + T * n_x / num * np.arange(num)确定,其中T = t[1] - t[0]。默认值为None。- axis整型, 可选
x的时间/频率轴,沿着该轴进行重采样。默认值为0。
- window类数组, 可调用对象, 字符串, 浮点数, 或元组, 可选
如果不是
None,则指定一个傅里叶域中的滤波器,在重采样前应用。即,x的FFTX通过X = W * fft(x, axis=axis)计算。W可以被解释为光谱窗函数W(f_X),它使用频率f_X = fftfreq(n_x, T)。如果window是一个长度为
n_x的一维数组,则W=window。如果window是可调用对象,则W = window(f_X)。否则,window会传递给get_window,即W = fftshift(signal.get_window(window, n_x))。默认值为None。- domain‘time’ | ‘freq’, 可选
如果设置为
'time'(默认),则对x应用FFT;否则('freq'),假定FFT已应用于x,即x = fft(x_t, axis=axis),其中x_t是时域输入信号。
- 返回:
- x_rndarray
由num个样本和采样间隔
T * n_x / num组成的重采样信号。- t_rndarray, 可选
x_r的num个等距时间戳。仅当参数t不是
None时返回。
另请参阅
decimate在应用FIR或IIR滤波器后,对(周期/非周期)信号进行降采样。
resample_poly使用多相滤波和FIR滤波器,对(周期/非周期)信号进行重采样。
备注
如果x是实数值且在时域中,此函数使用更高效的单边FFT,即
rfft/irfft。否则,使用双边FFT,即fft/ifft(所有FFT函数均来自scipy.fft模块)。如果将window应用于实值x,则通过取负频率分量和正频率分量的平均值来确定单边频谱窗函数。这确保了实值信号和虚部为零的复信号得到相同的处理。即,传递x或传递
x.astype(np.complex128)会产生相同的数值结果。如果输入或输出样本的数量是素数或具有少量素因子,则由于使用FFT,此函数可能会很慢。请查阅
prev_fast_len和next_fast_len来确定高效的信号长度。另外,利用resample_poly计算中间信号(如下例所示)可以显著提高速度。resample旨在用于等距采样间隔的周期信号。对于非周期信号,resample_poly可能是更好的选择。有关非恒定采样间隔信号的重采样方法,请查阅scipy.interpolate模块。示例
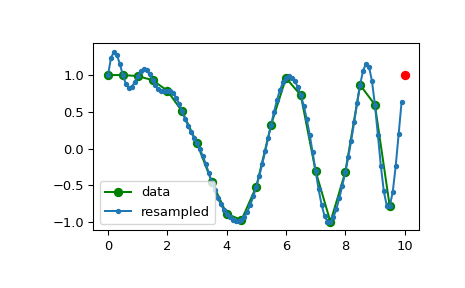
以下示例描述了一个信号从20个样本升采样到100个样本。升采样信号开头出现的振铃是由于将信号解释为周期性的。图中红色的方块通过显示信号下一个周期的第一个样本来解释周期性。
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.signal import resample ... >>> n0, n1 = 20, 100 # number of samples >>> t0 = np.linspace(0, 10, n0, endpoint=False) # input time stamps >>> x0 = np.cos(-t0**2/6) # input signal ... >>> x1 = resample(x0, n1) # resampled signal >>> t1 = np.linspace(0, 10, n1, endpoint=False) # timestamps of x1 ... >>> fig0, ax0 = plt.subplots(1, 1, tight_layout=True) >>> ax0.set_title(f"Resampling $x(t)$ from {n0} samples to {n1} samples") >>> ax0.set(xlabel="Time $t$", ylabel="Amplitude $x(t)$") >>> ax0.plot(t1, x1, '.-', alpha=.5, label=f"Resampled") >>> ax0.plot(t0, x0, 'o-', alpha=.5, label="Original") >>> ax0.plot(10, x0[0], 'rs', alpha=.5, label="Next Cycle") >>> ax0.legend(loc='best') >>> ax0.grid(True) >>> plt.show()
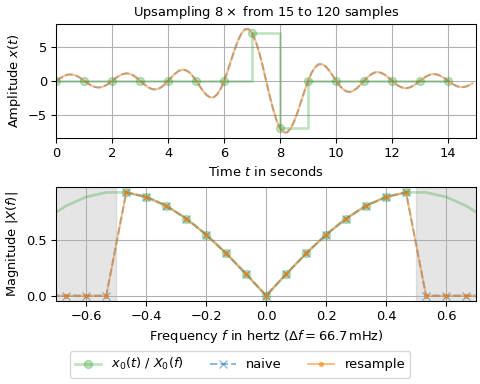
以下示例将此函数与朴素的
rfft/irfft组合进行比较:一个采样间隔为一秒的输入信号被升采样八倍。第一张图描绘了奇数个输入样本,而第二张图描绘了偶数个。上面的子图显示了信号随时间的变化:输入样本用大绿点标记,升采样信号用实线和虚线表示。下面的子图显示了幅度谱:输入的FFT值用大绿点表示,位于[-0.5, 0.5] Hz的频率区间内,而升采样信号的频率区间为[-4, 4] Hz。连续的绿线表示未经抗混叠滤波的升采样频谱,它是输入频谱的周期性延续。蓝色的“x”和橙色的点表示通过朴素方法以及本函数结果生成的信号的FFT值。>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.fft import fftshift, fftfreq, fft, rfft, irfft >>> from scipy.signal import resample, resample_poly ... >>> fac, T0, T1 = 8, 1, 1/8 # upsampling factor and sampling intervals >>> for n0 in (15, 16): # number of samples of input signal ... n1 = fac * n0 # number of samples of upsampled signal ... t0, t1 = T0 * np.arange(n0), T1 * np.arange(n1) # time stamps ... x0 = np.zeros(n0) # input signal has two non-zero sample values ... x0[n0//2], x0[n0//2+1] = n0 // 2, -(n0 // 2) ... ... x1n = irfft(rfft(x0), n=n1) * n1 / n0 # naive resampling ... x1r = resample(x0, n1) # resample signal ... ... # Determine magnitude spectrum: ... x0_up = np.zeros_like(x1r) # upsampling without antialiasing filter ... x0_up[::n1 // n0] = x0 ... X0, X0_up = (fftshift(fft(x_)) / n0 for x_ in (x0, x0_up)) ... XX1 = (fftshift(fft(x_)) / n1 for x_ in (x1n, x1r)) ... f0, f1 = fftshift(fftfreq(n0, T0)), fftshift(fftfreq(n1, T1)) # frequencies ... df = f0[1] - f0[0] # frequency resolution ... ... fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4)) ... ax0.set_title(rf"Upsampling ${fac}\times$ from {n0} to {n1} samples") ... ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", ... xlim=(0, n1*T1)) ... ax0.step(t0, x0, 'C2o-', where='post', alpha=.3, linewidth=2, ... label="$x_0(t)$ / $X_0(f)$") ... for x_, l_ in zip((x1n, x1r), ('C0--', 'C1-')): ... ax0.plot(t1, x_, l_, alpha=.5, label=None) ... ax0.grid() ... ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {df*1e3:.1f}\,$mHz)", ... ylabel="Magnitude $|X(f)|$", xlim=(-0.7, 0.7)) ... ax1.axvspan(0.5/T0, f1[-1], color='gray', alpha=.2) ... ax1.axvspan(f1[0], -0.5/T0, color='gray', alpha=.2) ... ax1.plot(f1, abs(X0_up), 'C2-', f0, abs(X0), 'C2o', alpha=.3, linewidth=2) ... for X_, n_, l_ in zip(XX1, ("naive", "resample"), ('C0x--', 'C1.-')): ... ax1.plot(f1, abs(X_), l_, alpha=.5, label=n_) ... ax1.grid() ... fig.legend(loc='outside lower center', ncols=4) >>> plt.show()
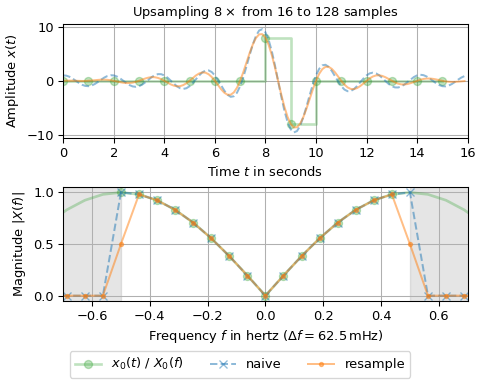
第一张图显示,对奇数个样本进行升采样会产生相同的结果。第二张图说明,通过朴素方法(蓝色虚线)从偶数个样本生成的信号并未触及所有原始样本。这种偏差是由于
resample正确处理了未配对的频率箱(bin)。即,输入x1有一对±0.5 Hz的频率箱,而输出在-0.5 Hz处只有一个未配对的频率箱,这要求对该频率箱对进行重新缩放。通常,如果n_x != num且min(n_x, num)为偶数,则需要特殊处理。如果±m处的频率箱值为零,则显然不需要特殊处理。有关详细信息,请查阅resample的源代码。最后一个示例展示了如何利用
resample_poly来加速降采样:输入信号在\(t=0\)处有一个非零值,并从19937个样本降采样到128个样本。由于19937是素数,FFT预计会很慢。为了加速,使用resample_poly先降采样因子为n0 // n1 = 155,然后将结果传递给resample。resample_poly使用了两种参数化方式:传递padtype='wrap'将输入视为周期性的,而默认参数化则执行零填充。上面的子图显示了随时间变化的信号结果,而下面的子图描绘了结果的单边幅度谱。>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.fft import rfftfreq, rfft >>> from scipy.signal import resample, resample_poly ... >>> n0 = 19937 # number of input samples - prime >>> n1 = 128 # number of output samples - fast FFT length >>> T0, T1 = 1/n0, 1/n1 # sampling intervals >>> t0, t1 = np.arange(n0)*T0, np.arange(n1)*T1 # time stamps ... >>> x0 = np.zeros(n0) # Input has one non-zero sample >>> x0[0] = n0 >>> >>> x1r = resample(x0, n1) # slow due to n0 being prime >>> # This is faster: >>> x1p = resample(resample_poly(x0, 1, n0 // n1, padtype='wrap'), n1) # periodic >>> x2p = resample(resample_poly(x0, 1, n0 // n1), n1) # with zero-padding ... >>> X0 = rfft(x0) / n0 >>> X1r, X1p, X2p = rfft(x1r) / n1, rfft(x1p) / n1, rfft(x2p) / n1 >>> f0, f1 = rfftfreq(n0, T0), rfftfreq(n1, T1) ... >>> fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4)) >>> ax0.set_title(f"Dowsampled Impulse response (from {n0} to {n1} samples)") >>> ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", xlim=(-T1, 1)) >>> for x_ in (x1r, x1p, x2p): ... ax0.plot(t1, x_, alpha=.5) >>> ax0.grid() >>> ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {f1[1]}\,$Hz)", ... ylabel="Magnitude $|X(f)|$", xlim=(0, 0.55/T1)) >>> ax1.axvspan(0.5/T1, f0[-1], color='gray', alpha=.2) >>> ax1.plot(f1, abs(X1r), 'C0.-', alpha=.5, label="resample") >>> ax1.plot(f1, abs(X1p), 'C1.-', alpha=.5, label="resample_poly(padtype='wrap')") >>> ax1.plot(f1, abs(X2p), 'C2x-', alpha=.5, label="resample_poly") >>> ax1.grid() >>> fig.legend(loc='outside lower center', ncols=2) >>> plt.show()
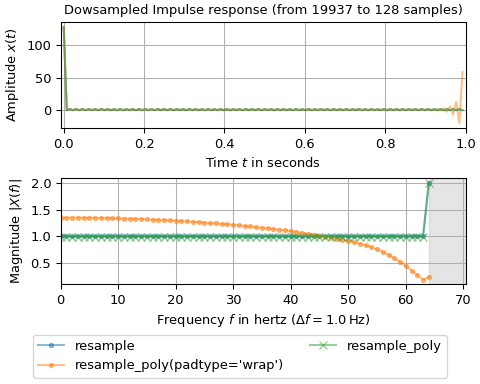
图中显示,“纯”
resample的结果与使用resample_poly默认参数的结果非常吻合。另一方面,resample_poly的周期性填充(padtype='wrap')产生了显著偏差。这是由于信号开头的间断性造成的,resample_poly的默认滤波器不适合处理这种情况。此示例说明,在某些用例中,调整resample_poly参数可能会有益。resample在这方面有一个很大的优势:它默认使用具有最大带宽的理想抗混叠滤波器。请注意,64 Hz奈奎斯特频率处的频谱幅度加倍是由于
n1=128的偶数个输出样本造成的,这需要特殊处理,如前一个示例中所讨论的。