scipy.fft.

fft#

scipy.fft.fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)[source]#

计算一维离散傅里叶变换。

此函数使用高效的快速傅里叶变换（FFT）算法 [1] 计算一维 *n*-点离散傅里叶变换（DFT）。

参数:

xarray_like: 输入数组，可以是复数。
nint, optional: 输出变换轴的长度。如果 n 小于输入长度，则输入会被裁剪。如果大于输入长度，则输入会用零填充。如果未给出 n，则使用输入沿 axis 指定轴的长度。
axisint, optional: 计算 FFT 的轴。如果未给出，则使用最后一个轴。
norm{“backward”, “ortho”, “forward”}, optional: 归一化模式。默认为“backward”，表示正向变换不进行归一化，ifft 则按 1/n 缩放。“forward”则在正向变换上应用 1/n 因子。对于 norm="ortho"，两个方向都按 1/sqrt(n) 缩放。

在版本 1.6.0 中新增: norm={"forward", "backward"} 选项已添加
overwrite_xbool, optional: 如果为 True，则 x 的内容可能会被销毁；默认为 False。详情请参阅下方注释。
workersint, optional: 用于并行计算的最大工作进程数。如果为负数，则值将从 os.cpu_count() 环绕。详情请参阅下方。
planobject, optional: 此参数保留用于传入由下游 FFT 供应商提供的预计算计划。SciPy 目前未使用此参数。

在版本 1.5.0 中新增。

返回:

outcomplex ndarray: 截断或零填充的输入，沿 axis 指示的轴进行变换，如果未指定 axis，则沿最后一个轴进行变换。

抛出:

IndexError: 如果 axes 大于 x 的最后一个轴。

另请参阅

ifft: fft 的逆变换。
fft2: 二维快速傅里叶变换。
fftn: N维快速傅里叶变换。
rfftn: 实数输入的 N维快速傅里叶变换。
fftfreq: 给定 FFT 参数的频率分量。
next_fast_len: 为实现最高效变换而对输入进行填充的大小

注释

FFT（快速傅里叶变换）是指利用计算项中的对称性高效计算离散傅里叶变换（DFT）的一种方法。当 n 是 2 的幂时，对称性最高，因此对于这些大小的变换效率最高。对于难以分解的大小，scipy.fft 使用 Bluestein 算法 [2]，因此性能绝不会比 O(n log n) 差。通过使用 next_fast_len 对输入进行零填充，可以进一步提高性能。

如果 x 是一个一维数组，则 fft 等价于

y[k] = np.sum(x * np.exp(-2j * np.pi * k * np.arange(n)/n))

频率项 f=k/n 位于 y[k]。在 y[n/2] 处，我们达到奈奎斯特频率并环绕到负频率项。因此，对于一个 8 点变换，结果的频率为 [0, 1, 2, 3, -4, -3, -2, -1]。要重新排列 fft 输出，使零频率分量居中，例如 [-4, -3, -2, -1, 0, 1, 2, 3]，请使用 fftshift。

变换可以使用单精度、双精度或扩展精度（长双精度）浮点数完成。半精度输入将被转换为单精度，非浮点输入将被转换为双精度。

如果 x 的数据类型是实数，将自动使用“实数 FFT”算法，这大约能将计算时间减半。为了进一步提高效率，可以使用 rfft，它进行相同的计算，但只输出对称频谱的一半。如果数据既是实数又是对称的，dct 可以再次将效率提高一倍，通过从信号的一半生成频谱的一半。

当指定 overwrite_x=True 时，实现可能会以任何方式使用 x 引用的内存。这可能包括重用结果的内存，但这绝不保证。在变换之后，您不应依赖 x 的内容，因为将来它可能会在不发出警告的情况下发生变化。

workers 参数指定了将 FFT 计算拆分为并行作业的最大数量。这将在 x 中执行独立的 1-D FFT。因此，x 必须至少是二维的，并且非变换轴必须足够大以便拆分为块。如果 x 太小，则使用的作业可能少于请求的数量。

参考文献

[1]

Cooley, James W., and John W. Tukey, 1965, “一种用于机器计算复数傅里叶级数的算法,” Math. Comput. 19: 297-301.

[2]

Bluestein, L., 1970, “一种用于计算离散傅里叶变换的线性滤波方法”. IEEE Transactions on Audio and Electroacoustics. 18 (4): 451-455.

示例

>>> import scipy.fft
>>> import numpy as np
>>> scipy.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

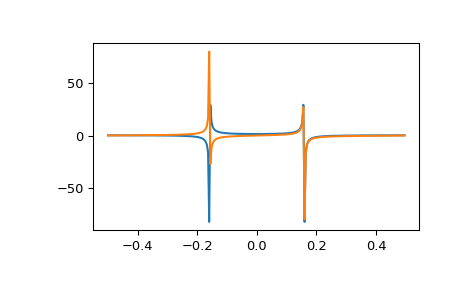
在此示例中，实数输入的 FFT 是厄米特的，即在实部对称，在虚部反对称

>>> from scipy.fft import fft, fftfreq, fftshift
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = fftshift(fft(np.sin(t)))
>>> freq = fftshift(fftfreq(t.shape[-1]))
>>> plt.plot(freq, sp.real, freq, sp.imag)
[<matplotlib.lines.Line2D object at 0x...>,
 <matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()