scipy.signal.

resample_poly

scipy.signal.resample_poly(x, up, down, axis=0, window=('kaiser', 5.0), padtype='constant', cval=None)

使用多相滤波沿给定轴对 x 进行重采样。

信号 x 通过因子 up 进行上采样，然后应用零相位低通 FIR 滤波器，再通过因子 down 进行下采样。最终采样率是原始采样率的 up / down 倍。默认情况下，在滤波步骤中，信号边界之外的值被假定为零。

参数:

x类数组

要重采样的数据。

up整型

上采样因子。

down整型

下采样因子。

axis整型, 可选

对 x 进行重采样的轴。默认为 0。

window字符串、元组或类数组, 可选

用于设计低通滤波器的所需窗函数，或要使用的 FIR 滤波器系数。详见下文。

padtype字符串, 可选

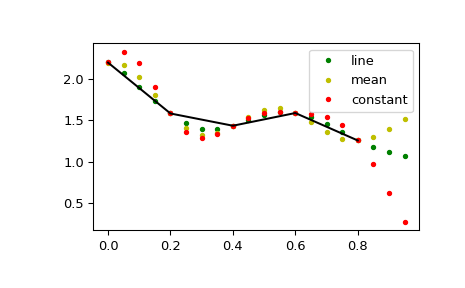
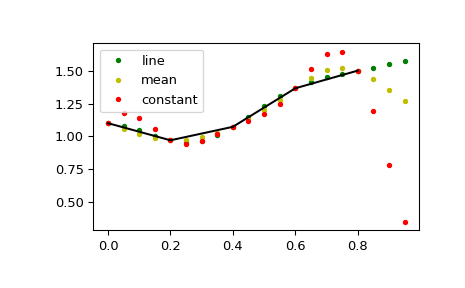
constant（常数）, line（线型）, mean（均值）, median（中位数）, maximum（最大值）, minimum（最小值），或 scipy.signal.upfirdn 支持的任何其他信号扩展模式。更改对边界外值的假设。如果为 constant，则假定为 cval（默认零）。如果为 line，则假定为由第一个和最后一个点定义的线性趋势的延续。mean、median、maximum 和 minimum 的工作方式与 np.pad 相同，假定边界外的值分别是数组沿该轴的均值、中位数、最大值或最小值。

在 1.4.0 版本中新增。

cval浮点型, 可选

如果 padtype=’constant’，则使用的值。默认为零。

在 1.4.0 版本中新增。

返回值:

resampled_x数组

重采样后的数组。

另请参阅

decimate

在应用 FIR 或 IIR 滤波器后对信号进行下采样。

resample

使用 FFT 方法进行上采样或下采样。

说明

当样本数量大且为素数时，或者当样本数量大且 up 和 down 具有较大公约数时，此多相方法可能比 scipy.signal.resample 中的傅里叶方法更快。所使用的 FIR 滤波器的长度将取决于 max(up, down) // gcd(up, down)，多相滤波期间的操作次数将取决于滤波器长度和 down（详见 scipy.signal.upfirdn）。

参数 window 指定了 FIR 低通滤波器的设计。

如果 window 是一个类数组，则假定它是 FIR 滤波器系数。请注意，FIR 滤波器是在上采样步骤之后应用的，因此应设计为在采样频率高于原始频率 up//gcd(up, down) 倍的信号上运行。此函数的输出将相对于此数组居中，因此，如果通常需要零相位滤波器，最好传递一个具有奇数个样本的对称滤波器。

对于任何其他类型的 window，将调用函数 scipy.signal.get_window 和 scipy.signal.firwin 来生成相应的滤波器系数。

返回向量的第一个样本与输入向量的第一个样本相同。样本之间的间距从 dx 变为 dx * down / float(up)。

示例

在浏览器中尝试！

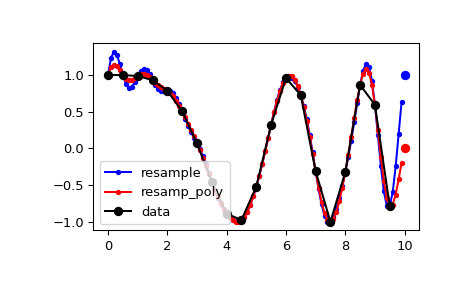
默认情况下，对于 FFT 方法，重采样数据的末尾会上升以与下一个周期的第一个样本会合；对于多相方法，则趋近于零。

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(0, 10, 20, endpoint=False)
>>> y = np.cos(-x**2/6.0)
>>> f_fft = signal.resample(y, 100)
>>> f_poly = signal.resample_poly(y, 100, 20)
>>> xnew = np.linspace(0, 10, 100, endpoint=False)

>>> plt.plot(xnew, f_fft, 'b.-', xnew, f_poly, 'r.-')
>>> plt.plot(x, y, 'ko-')
>>> plt.plot(10, y[0], 'bo', 10, 0., 'ro')  # boundaries
>>> plt.legend(['resample', 'resamp_poly', 'data'], loc='best')
>>> plt.show()

此默认行为可以通过使用 padtype 选项进行更改

>>> N = 5
>>> x = np.linspace(0, 1, N, endpoint=False)
>>> y = 2 + x**2 - 1.7*np.sin(x) + .2*np.cos(11*x)
>>> y2 = 1 + x**3 + 0.1*np.sin(x) + .1*np.cos(11*x)
>>> Y = np.stack([y, y2], axis=-1)
>>> up = 4
>>> xr = np.linspace(0, 1, N*up, endpoint=False)

>>> y2 = signal.resample_poly(Y, up, 1, padtype='constant')
>>> y3 = signal.resample_poly(Y, up, 1, padtype='mean')
>>> y4 = signal.resample_poly(Y, up, 1, padtype='line')

>>> for i in [0,1]:
...     plt.figure()
...     plt.plot(xr, y4[:,i], 'g.', label='line')
...     plt.plot(xr, y3[:,i], 'y.', label='mean')
...     plt.plot(xr, y2[:,i], 'r.', label='constant')
...     plt.plot(x, Y[:,i], 'k-')
...     plt.legend()
>>> plt.show()

返回在新标签页中打开