spectrogram#
- scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, mode='psd')[source]#
使用连续傅里叶变换计算频谱图(遗留函数)。
频谱图可用于可视化非平稳信号频率内容随时间的变化。
遗留功能
此函数被视为遗留功能,将不再接收更新。虽然我们目前没有移除它的计划,但建议新代码改用更现代的替代方案。
ShortTimeFFT是一个更新的 STFT / ISTFT 实现,具有更多功能,也包括一个spectrogram方法。有关这些实现之间的比较,请参阅 SciPy 用户指南的短时傅里叶变换部分。- 参数:
- xarray_like
测量值的时间序列
- fsfloat, optional
x 时间序列的采样频率。默认为 1.0。
- windowstr or tuple or array_like, optional
要使用的所需窗函数。如果 window 是字符串或元组,它将传递给
get_window以生成窗函数值,这些值默认是 DFT-偶数的。有关窗函数列表和所需参数,请参阅get_window。如果 window 是 array_like,它将直接用作窗函数,并且其长度必须为 nperseg。默认为形状参数为 0.25 的 Tukey 窗函数。- npersegint, optional
每个段的长度。默认为 None,但如果 window 是 str 或 tuple,则设置为 256;如果 window 是 array_like,则设置为窗函数的长度。
- noverlapint, optional
段之间重叠的点数。如果为 None,则
noverlap = nperseg // 8。默认为 None。- nfftint, optional
使用的 FFT 长度,如果需要零填充 FFT。如果为 None,则 FFT 长度为 nperseg。默认为 None。
- detrendstr or function or False, optional
指定如何对每个段进行去趋势。如果
detrend是字符串,则作为 type 参数传递给detrend函数。如果它是一个函数,它接受一个段并返回一个去趋势的段。如果detrend为 False,则不进行去趋势。默认为 ‘constant’。- return_onesidedbool, optional
如果为 True,则返回实数数据的一侧频谱。如果为 False,则返回双侧频谱。默认为 True,但对于复数数据,总是返回双侧频谱。
- scaling{ ‘density’, ‘spectrum’ }, optional
选择计算功率谱密度(‘density’),此时 Sxx 的单位为 V**2/Hz;或计算功率谱(‘spectrum’),此时 Sxx 的单位为 V**2(如果 x 以 V 为单位测量,fs 以 Hz 为单位测量)。默认为 ‘density’。
- axisint, optional
计算频谱图的轴;默认为最后一个轴(即
axis=-1)。- modestr, optional
定义预期返回值的类型。选项有 [‘psd’, ‘complex’, ‘magnitude’, ‘angle’, ‘phase’]。“complex”等同于不进行填充或边界扩展的
stft输出。“magnitude”返回 STFT 的绝对幅值。“angle”和“phase”分别返回 STFT 的复数角度(带或不带解卷绕)。
- 返回值:
- fndarray
采样频率数组。
- tndarray
段时间数组。
- Sxxndarray
x 的频谱图。默认情况下,Sxx 的最后一个轴对应于段时间。
另请参阅
periodogram简单、可选修改的周期图
lombscargle用于不均匀采样数据的 Lomb-Scargle 周期图
welch基于 Welch 方法的功率谱密度。
csd基于 Welch 方法的互谱密度。
ShortTimeFFT提供更多功能的新型 STFT/ISTFT 实现,其中也包括一个
spectrogram方法。
注释
适当的重叠量将取决于窗函数的选择和您的要求。与 Welch 方法(对整个数据流进行平均)不同,在计算频谱图时,可能希望使用较小的重叠(或完全不重叠),以保持各个段之间的一些统计独立性。正是出于这个原因,默认的窗函数是一个 Tukey 窗,其两端各重叠窗函数长度的 1/8。
在 0.16.0 版本中添加。
参考文献
[1]Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time Signal Processing”, Prentice Hall, 1999.
示例
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fftshift >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()
生成一个测试信号:一个 2 Vrms 正弦波,其频率在 3kHz 附近缓慢调制,并受到幅度呈指数衰减的白噪声干扰,采样频率为 10 kHz。
>>> fs = 10e3 >>> N = 1e5 >>> amp = 2 * np.sqrt(2) >>> noise_power = 0.01 * fs / 2 >>> time = np.arange(N) / float(fs) >>> mod = 500*np.cos(2*np.pi*0.25*time) >>> carrier = amp * np.sin(2*np.pi*3e3*time + mod) >>> noise = rng.normal(scale=np.sqrt(noise_power), size=time.shape) >>> noise *= np.exp(-time/5) >>> x = carrier + noise
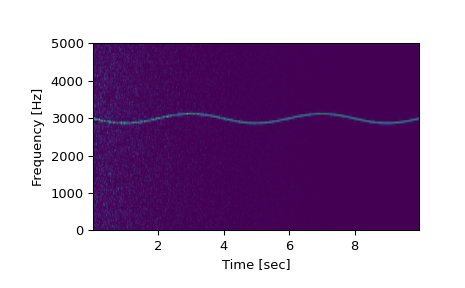
计算并绘制频谱图。
>>> f, t, Sxx = signal.spectrogram(x, fs) >>> plt.pcolormesh(t, f, Sxx, shading='gouraud') >>> plt.ylabel('Frequency [Hz]') >>> plt.xlabel('Time [sec]') >>> plt.show()
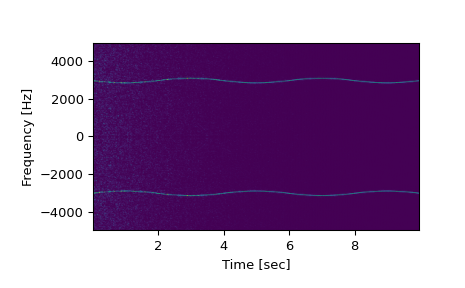
注意,如果使用非单侧输出,请使用以下方法
>>> f, t, Sxx = signal.spectrogram(x, fs, return_onesided=False) >>> plt.pcolormesh(t, fftshift(f), fftshift(Sxx, axes=0), shading='gouraud') >>> plt.ylabel('Frequency [Hz]') >>> plt.xlabel('Time [sec]') >>> plt.show()