scipy.signal.ShortTimeFFT.

from_win_equals_dual

classmethod ShortTimeFFT.from_win_equals_dual(desired_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)

创建一个实例，其中窗口及其对偶（dual）在缩放因子范围内相等。

创建一个实例，其中窗口和对偶窗口相等，并且在最小二乘意义上最接近参数 desired_win，即最小化 abs(win-desired_win)**2。因此，win 的长度与 desired_win 相同。然后根据 scale_to 参数应用一个缩放因子。

所有其他参数的含义与初始化器中的含义相同。

为了能够计算一个有效的窗口，desired_win 需要为给定的 hop 间隔具有一个有效的对偶 STFT 窗口。如果不是这种情况，则会引发 ValueError。

参数:

desired_winnp.ndarray

一个实值或复值的一维数组，包含所需窗口的样本。

hopint

样本中的增量，即窗口每步移动的量。

fsfloat

输入信号和窗口的采样频率。它与采样间隔 T 的关系是 T = 1 / fs。

fft_mode‘twosided’, ‘centered’, ‘onesided’, ‘onesided2X’

要使用的 FFT 模式（默认为 'onesided'）。有关详细信息，请参见属性 fft_mode。

mfft: int | None

如果需要零填充 FFT，则为所使用的 FFT 长度。如果为 None（默认值），则使用窗口 win 的长度。

scale_to‘magnitude’ | ‘psd’ | ‘unitary’ | None

如果不是 None（默认值），则对窗口函数进行缩放，使每个 STFT 列代表“幅度”（'magnitude'）或功率谱密度（'psd'）频谱。或者，STFT 可以缩放到“单一”映射（'unitary' mapping），即窗口除以 np.sqrt(mfft)，并将对偶窗口乘以相同的值。

phase_shiftint | None

如果设置，则为每个频率 f 添加一个线性相位 phase_shift / mfft * f。默认值 0 确保在第零切片（t=0 居中）上没有相位偏移。有关更多详细信息，请参见属性 phase_shift。

另请参见

closest_STFT_dual_window

计算给定窗口最接近所需对偶窗口的 STFT 对偶窗口。

ShortTimeFFT.spectrogram

计算平方 STFTs

ShortTimeFFT

此属性所属的类。

备注

具有相同对偶的所有可能窗口的集合由 SciPy 用户指南 中 短时傅里叶变换 部分的等式 (24) 的线性约束集合定义。在该部分还推导出，为了使 STFT 成为单一映射，ShortTimeFFT.dual_win == ShortTimeFFT.m_pts * ShortTimeFFT.win 必须成立。

单一映射保留了标量积的值，即：

\[\langle x, y\rangle = \sum_k x[k]\, \overline{y[k]} \stackrel{\stackrel{\text{unitary}}{\downarrow}}{=} \sum_{q,p} S_x[q,p]\, \overline{S_y[q,p]} = \langle S_x[q,p], S_y[q,p]\rangle\ ,\]

其中 \(S_{x,y}\) 是 \(x,y\) 的 STFT。因此，信号的能量 \(E_x=T\sum_k |x[k]|^2\) 也得以保留。这在下面的示例中也有说明。

区分不缩放（即参数 scale_to 为 None）和单一缩放（即 scale_to = 'unitary'）的原因是所使用的 FFT 函数并非单一（即，fft 参数 norm 使用默认值 'backward'）。

示例

在浏览器中尝试！

以下示例表明 STFT 确实可以是单一的

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import ShortTimeFFT, windows
...
>>> m, hop, std = 36, 8, 5
>>> desired_win = windows.gaussian(m, std, sym=True)
>>> SFT = ShortTimeFFT.from_win_equals_dual(desired_win, hop, fs=1/m,
...                                         fft_mode='twosided',
...                                         scale_to='unitary')
>>> np.allclose(SFT.dual_win, SFT.win * SFT.m_num)  # check if STFT is unitary
True
>>> x1, x2 = np.tile([-1, -1, 1, 1], 5), np.tile([1, -1, -1, 1], 5)
>>> np.sum(x1*x2) # scalar product is zero -> orthogonal signals
0
>>> np.sum(x1**2)  # scalar product of x1 with itself
20
>>> Sx11, Sx12 = SFT.spectrogram(x1), SFT.spectrogram(x1, x2)
>>> np.sum(Sx12)  # STFT scalar product is also zero
-4.163336342344337e-16+0j  # may vary
>>> np.sum(Sx11)  # == np.sum(x1**2)
19.999999999999996  # may vary
...
... # Do the plotting:
>>> fg1, (ax11, ax12) = plt.subplots(1, 2, tight_layout=True, figsize=(8, 4))
>>> s_fac = np.sqrt(SFT.mfft)
>>> _ = fg1.suptitle(f"Scaled Unitary Window of {m} Sample Gaussian with " +
...                  rf"{hop=}, $\sigma={std}$, Scale factor: {s_fac}")
>>> ax11.set(ylabel="Amplitude", xlabel="Samples", xlim=(0, m))
>>> ax12.set(xlabel="Frequency Bins", ylabel="Magnitude Spectrum",
...          xlim=(0, 15), ylim=(1e-5, 1.5))
>>> u_win_str = rf"Unitary $\times{s_fac:g}$"
>>> for x_, n_ in zip((desired_win, SFT.win*s_fac), ('Desired', u_win_str)):
...     ax11.plot(x_, '.-', alpha=0.5, label=n_)
...     X_ = np.fft.rfft(x_) / np.sum(abs(x_))
...     ax12.semilogy(abs(X_), '.-', alpha=0.5, label=n_)
>>> for ax_ in (ax11, ax12):
...     ax_.grid(True)
...     ax_.legend()
>>> plt.show()

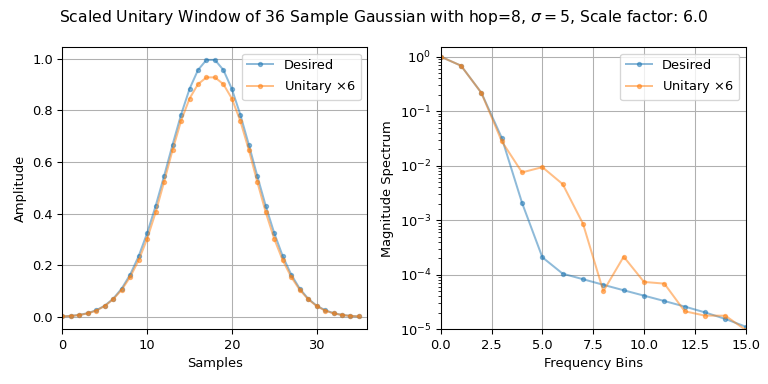
请注意，使用了 fftmode='twosided'，因为我们需要对完整时频平面求和。由于传递了 scale_to='unitary'，窗口 SFT.win 会按 1/np.sqrt(SFT.mfft) 进行缩放。因此，在上面的图中，SFT.win 需要按 s_fac 进行缩放。

返回在新标签页中打开