scipy.signal.

closest_STFT_dual_window#

scipy.signal.closest_STFT_dual_window(win, hop, desired_dual=None, *, scaled=True)[源码]#

计算给定窗口的 STFT 双窗口，使其最接近于所需的双窗口。

对于给定按 hop 采样递增的短时傅里叶变换窗口 win，将计算其双窗口，该双窗口在 scaled 为 False 时使 abs(dual_win - desired_dual)**2 最小化。如果 scaled 设置为 True，则以 alpha 作为最佳缩放因子，使 abs(alpha*dual_win - desired_dual)**2 最小化。如果无法确定有效的双窗口，则会引发 ValueError。

参数:

winnp.ndarray: 窗口必须是实值或复值的 1 维数组。
hopint: 窗口在每一步中移动的采样增量。
desired_dual: np.ndarray | None: 所需的双窗口必须是与 win 长度相同的 1 维数组。如果设置为 None（默认），则 desired_dual 假定为矩形窗口，即 np.ones_like(win)。
scaledbool: 如果设置（默认），则计算最接近的缩放版本而不是最接近的双窗口。

返回:

dual_winnp.ndarray: 一个 alpha*win 的双窗口（跳跃间隔为 hop），它最接近 desired_dual。请注意，win 的双窗口是 dual_win/alpha，而 dual_win 的双窗口是 alpha*win。dual_win 具有与 win 和 desired_win 相同的形状。
alphafloat | complex: win 的缩放因子。如果 scaled 设置为 False，则其始终为一。

另请参阅

ShortTimeFFT: 短时傅里叶变换，能够利用双窗口计算逆变换。
ShortTimeFFT.from_win_equals_dual: 创建窗口及其双窗口相等的实例。

注意

对于给定的窗口和 hop 间隔，所有可能的双窗口均由短时傅里叶变换一节中 SciPy 用户指南的等式 (24) 的 hop 线性条件表示。因此，减小 hop 会增加所有可能双窗口集合的自由度数量，从而提高更好地近似 desired_dual 的能力。

此函数也可用于确定满足所谓“恒定重叠相加”（COLA）条件 [1] 的窗口。它指出在任何给定采样位置处将所有相邻窗口值相加，结果为相同的常数 \(\alpha\)。等式 (24) 表明这等同于拥有一个矩形双窗口，即双窗口为 alpha*np.ones(m)。

满足 COLA 条件的一些窗口示例（摘自 [2]）

重叠率为 0, 1/2, 2/3, 3/4, … 时的矩形窗口
重叠率为 1/2, 3/4, 5/6, … 时的 Bartlett 窗口
重叠率为 1/2, 2/3, 3/4, … 时的 Hann 窗口
重叠率为 2/3 时的任何 Blackman 族窗口
任何 hop=1 的窗口

参考文献

[1]

Julius O. Smith III，“频谱音频信号处理”，在线书籍，2011，https://www.dsprelated.com/freebooks/sasp/

[2]

G. Heinzel, A. Ruediger 和 R. Schilling，“通过离散傅里叶变换 (DFT) 进行频谱和谱密度估计，包括窗口函数的完整列表和一些新的顶部窗口”，2002，http://hdl.handle.net/11858/00-001M-0000-0013-557A-5

示例

让我们证明一个具有 75% 重叠的 Bartlett 窗口满足 COLA 条件

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import closest_STFT_dual_window, windows
...
>>> m = 24
>>> win, w_rect = windows.bartlett(m, sym=False), np.ones(m)
>>> d_win, alpha = closest_STFT_dual_window(win, m//4, w_rect, scaled=True)
>>> print(f"COLA: {np.allclose(d_win, w_rect*alpha)}, {alpha = :g}")
COLA: True, alpha = 0.5

我们还可以确定 COLA 条件对于哪些跳跃间隔是满足的

>>> hops, deviations, alphas = np.arange(1, 16, dtype=int), [], []
>>> for h_ in hops:
...     w_cola, alpha = closest_STFT_dual_window(w_rect, h_, win, scaled=True)
...     deviations.append(np.linalg.norm(w_cola - win*alpha))
...     alphas.append(alpha)
...
>>> fg0, (ax0, ax1) = plt.subplots(2, 1, sharex='all', tight_layout=True)
>>> ax0.set_title(f"COLA Window closest to a {m}-Sample Bartlett Window")
>>> ax0.set(ylabel=r"$||w_\text{cola}-\alpha w||$", xlim=(0, hops[-1]-.5))
>>> ax1.set(xlabel="Hop Interval", ylabel=r"Scaling factor $\alpha$",
...         ylim=(0, 1.25))
>>> ax0.plot(hops, deviations, 'C0.-')
>>> ax1.plot(hops, alphas, 'C1.-')
>>> for ax_ in (ax0, ax1):
...     ax_.grid()
>>> plt.show()

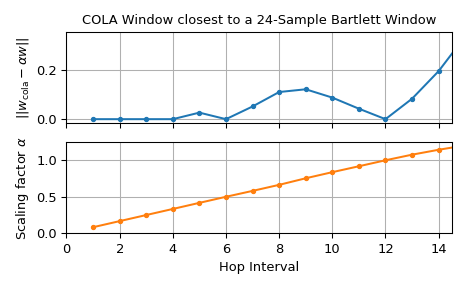
../../_images/scipy-signal-closest_STFT_dual_window-1_00_00.png

下部图显示了不同 hops 对应的计算缩放因子 \(\alpha\)，而上部图显示了缩放的 Bartlett 窗口与计算窗口之间差异的 \(L^2\)-范数。由于对于 hops 1 到 4 以及 6 和 12，差异的 \(L^2\)-范数实际上为零，因此这些情况下 COLA 条件得到满足。