scipy.signal.
lfilter#
- scipy.signal.lfilter(b, a, x, axis=-1, zi=None)[源]#
使用IIR或FIR滤波器沿一维过滤数据。
使用数字滤波器过滤数据序列x。这适用于许多基本数据类型(包括Object类型)。该滤波器是标准差分方程的直接II型转置实现(参见备注)。
对于大多数滤波任务,应优先使用函数
sosfilt(以及使用output='sos'的滤波器设计),因为二阶节具有较少的数值问题。- 参数:
- b类数组
一维序列中的分子系数向量。
- a类数组
一维序列中的分母系数向量。如果
a[0]不为1,则a和b都将通过a[0]进行归一化。- x类数组
N维输入数组。
- axisint, 可选
沿输入数据数组应用线性滤波器的轴。滤波器将沿此轴应用于每个子数组。默认值为-1。
- zi类数组, 可选
滤波器延迟的初始条件。它是一个长度为
max(len(a), len(b)) - 1的向量(或N维输入的向量数组)。如果zi为None或未给出,则假定初始静止状态。有关更多信息,请参阅lfiltic。
- 返回:
- y数组
数字滤波器的输出。
- zf数组, 可选
如果zi为None,则不返回此值;否则,zf保存最终的滤波器延迟值。
另请参阅
lfiltic为
lfilter构造初始条件。lfilter_zi计算
lfilter的初始状态(阶跃响应的稳态)。filtfilt一种正向-反向滤波器,用于获得零相位滤波器。
savgol_filter一种Savitzky-Golay滤波器。
sosfilt使用级联二阶节滤波数据。
sosfiltfilt一种使用二阶节的正向-反向滤波器。
备注
此滤波器函数实现为直接II型转置结构。这意味着该滤波器实现了
a[0]*y[n] = b[0]*x[n] + b[1]*x[n-1] + ... + b[M]*x[n-M] - a[1]*y[n-1] - ... - a[N]*y[n-N]
其中M是分子阶数,N是分母阶数,n是样本数。它使用以下差分方程实现(假设M = N)
a[0]*y[n] = b[0] * x[n] + d[0][n-1] d[0][n] = b[1] * x[n] - a[1] * y[n] + d[1][n-1] d[1][n] = b[2] * x[n] - a[2] * y[n] + d[2][n-1] ... d[N-2][n] = b[N-1]*x[n] - a[N-1]*y[n] + d[N-1][n-1] d[N-1][n] = b[N] * x[n] - a[N] * y[n]
其中d是状态变量。
在z变换域中描述此滤波器的有理传递函数为
-1 -M b[0] + b[1]z + ... + b[M] z Y(z) = -------------------------------- X(z) -1 -N a[0] + a[1]z + ... + a[N] z
示例
生成要滤波的噪声信号
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> t = np.linspace(-1, 1, 201) >>> x = (np.sin(2*np.pi*0.75*t*(1-t) + 2.1) + ... 0.1*np.sin(2*np.pi*1.25*t + 1) + ... 0.18*np.cos(2*np.pi*3.85*t)) >>> xn = x + rng.standard_normal(len(t)) * 0.08
创建一个3阶低通巴特沃斯滤波器
>>> b, a = signal.butter(3, 0.05)
将滤波器应用于xn。使用lfilter_zi选择滤波器的初始条件
>>> zi = signal.lfilter_zi(b, a) >>> z, _ = signal.lfilter(b, a, xn, zi=zi*xn[0])
再次应用滤波器,以获得与filtfilt相同阶数的滤波结果
>>> z2, _ = signal.lfilter(b, a, z, zi=zi*z[0])
使用filtfilt应用滤波器
>>> y = signal.filtfilt(b, a, xn)
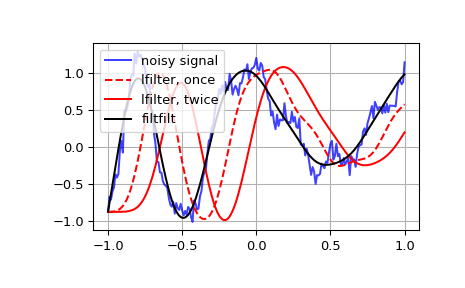
绘制原始信号和各种滤波后的版本
>>> plt.figure >>> plt.plot(t, xn, 'b', alpha=0.75) >>> plt.plot(t, z, 'r--', t, z2, 'r', t, y, 'k') >>> plt.legend(('noisy signal', 'lfilter, once', 'lfilter, twice', ... 'filtfilt'), loc='best') >>> plt.grid(True) >>> plt.show()