scipy.signal.

filtfilt#

scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)[源代码]#

对信号向前与向后使用数字滤波。

此函数对线性数字滤波使用两次，一次向前和一次向后。合成后的滤波器相位为零，并且滤波阶数是原始滤波器阶数的两倍。

此函数提供了用于处理信号边缘的选项。

大多数过滤任务应当优先使用函数 sosfiltfilt（和带有 output='sos' 的滤波器设计）而不是 filtfilt，因为二阶部分会产生较少数值问题。

参数:

b(N,) 类似数组: 滤波器的分子系数向量。
a(N,) 类似数组: 滤波器的分母系数向量。如果a[0]不是 1，那么a 和b 都将按a[0]归一化。
x类似数组: 要过滤的数据数组。
axisint，可选: 将滤波器应用到的x的轴。默认为 -1。
padtypestr 或 None，可选: 必须是“odd”、“even”、“constant”或 None。这决定了应用滤波器的填充信号的扩展类型。如果padtype为 None，则不使用填充。默认为“odd”。
padlenint 或 None，可选: 应用滤波器之前，在axis的两端扩展x的元素数量。此值必须小于x.shape[axis] - 1。 padlen=0表示不填充。默认值为3 * max(len(a), len(b))。
methodstr，可选: 确定处理信号边缘的方法，包括“pad”或“gust”。当method为“pad”时，填充信号；填充类型由padtype和padlen确定，并忽略irlen。当method为“gust”时，使用 Gustafsson’s 方法，并忽略padtype和padlen。
irlenint 或 None，可选: 当method为“gust”时，irlen指定滤波器的脉冲响应的长度。如果irlen为 None，则不忽略脉冲响应的任何部分。对于较长的信号，指定irlen可以显著提高滤波器的性能。

返回 :

yndarray: 过滤输出与x的形状相同。

另请参阅

sosfiltfilt、lfilter_zi、lfilter、lfiltic、savgol_filter、sosfilt

备注

当method为“pad”时，函数会以三种方式之一填充给定轴上的数据：奇数、偶数或常数。奇数和偶数扩展在数据终点周围具有相应对称性。常数扩展使用终点处的值扩展数据。在正向和反向遍历中，均通过使用lfilter_zi并按扩展数据的终点进行缩放来找到滤波器的初始条件。

当method为“gust”时，可以使用 Gustafsson 方法 [1]。为正向和反向遍历选择初始条件，以便正向反向滤波器和反向正向滤波器得到相同的结果。

Gustaffson 方法选项添加于 scipy 版本 0.16.0 中。

参考

[1]

F. Gustaffson，"Determining the initial states in forward-backward filtering"，Transactions on Signal Processing，第 46 卷，第 988-992 页，1996 年。

示例

这些示例将使用 scipy.signal 中的多个函数。

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

首先，我们创建一个一秒的信号，它是两个纯正弦波的总和，频率分别为 5 Hz 和 250 Hz，采样频率为 2000 Hz。

>>> t = np.linspace(0, 1.0, 2001)
>>> xlow = np.sin(2 * np.pi * 5 * t)
>>> xhigh = np.sin(2 * np.pi * 250 * t)
>>> x = xlow + xhigh

现在创建一个截止频率为奈奎斯特频率 0.125 倍（或 125 Hz）的低通巴特沃斯滤波器，并使用filtfilt将其应用于x。结果应近似为xlow，且无相移。

>>> b, a = signal.butter(8, 0.125)
>>> y = signal.filtfilt(b, a, x, padlen=150)
>>> np.abs(y - xlow).max()
9.1086182074789912e-06

对于这个人工示例，我们得到一个相当干净的结果，因为奇扩展是精确的，且通过适度延长填充，当实际数据到来时滤波器的瞬变就已经消散了。通常情况下，边缘处的瞬态效应是不可避免的。

下面的示例演示了选项 method="gust"。

首先，创建一个滤波器。

>>> b, a = signal.ellip(4, 0.01, 120, 0.125)  # Filter to be applied.

sig 是要过滤的随机输入信号。

>>> rng = np.random.default_rng()
>>> n = 60
>>> sig = rng.standard_normal(n)**3 + 3*rng.standard_normal(n).cumsum()

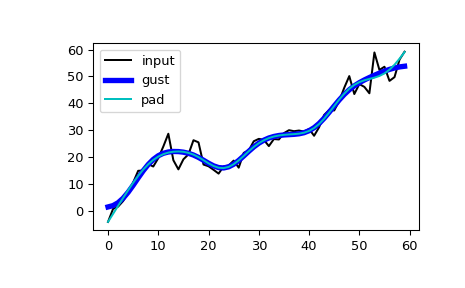
将 filtfilt 应用于 sig，一次使用 Gustafsson 方法，一次使用填充，然后绘制结果以进行比较。

>>> fgust = signal.filtfilt(b, a, sig, method="gust")
>>> fpad = signal.filtfilt(b, a, sig, padlen=50)
>>> plt.plot(sig, 'k-', label='input')
>>> plt.plot(fgust, 'b-', linewidth=4, label='gust')
>>> plt.plot(fpad, 'c-', linewidth=1.5, label='pad')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-signal-filtfilt-1_00_00.png

irlen 参数可用于提高 Gustafsson 方法的性能。

估算滤波器的冲击响应长度。

>>> z, p, k = signal.tf2zpk(b, a)
>>> eps = 1e-9
>>> r = np.max(np.abs(p))
>>> approx_impulse_len = int(np.ceil(np.log(eps) / np.log(r)))
>>> approx_impulse_len
137

将滤波器应用于一个较长的信号，无论是否带有 irlen 参数。 y1 和 y2 之间的差异很小。对于长信号，使用 irlen 可显着提高性能。

>>> x = rng.standard_normal(4000)
>>> y1 = signal.filtfilt(b, a, x, method='gust')
>>> y2 = signal.filtfilt(b, a, x, method='gust', irlen=approx_impulse_len)
>>> print(np.max(np.abs(y1 - y2)))
2.875334415008979e-10