scipy.signal.

sosfilt#

scipy.signal.sosfilt(sos, x, axis=-1, zi=None)[源码]#

使用级联二阶分段沿一个维度过滤数据。

使用由 sos 定义的数字 IIR 滤波器过滤数据序列 x。

参数:

sos类数组: 二阶滤波器系数数组，必须具有形状 `(n_sections, 6)`。每行对应一个二阶分段，前三列提供分子系数，后三列提供分母系数。
x类数组: 一个 N 维输入数组。
axis整型，可选: 应用线性滤波器的输入数据数组的轴。滤波器沿此轴应用于每个子数组。默认值为 -1。
zi类数组，可选: 级联滤波器延迟的初始条件。它是一个（至少 2D）向量，形状为 `(n_sections, ..., 2, ...)`，其中 `..., 2, ...` 表示 x 的形状，但 `x.shape[axis]` 被 2 替换。如果未给定 zi 或为 None，则假定初始静止（即全零）。请注意，这些初始条件与 lfiltic 或 lfilter_zi 给出的初始条件不同。


返回:

yndarray
数字滤波器的输出。

zfndarray, 可选
如果 zi 为 None，则不返回此项；否则，zf 保存最终的滤波器延迟值。



另请参阅

zpk2sos, sos2zpk, sosfilt_zi, sosfiltfilt, freqz_sos



备注
此滤波器函数以一系列具有直接形式 II 转置结构的二阶滤波器实现。它旨在最大限度地减少高阶滤波器的数值精度误差。

0.16.0 版中新增。

示例


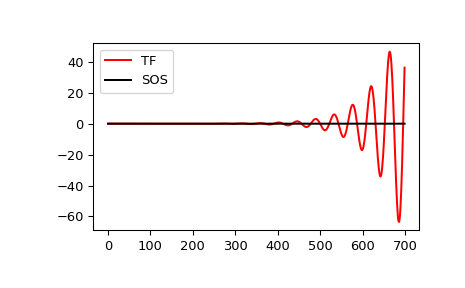
使用 lfilter 和 sosfilt 绘制 13 阶滤波器的脉冲响应，展示了尝试单级实现 13 阶滤波器导致的不稳定性（数值误差将一些极点推到了单位圆之外）
>>> import matplotlib.pyplot as plt
>>> from scipy import signal
>>> b, a = signal.ellip(13, 0.009, 80, 0.05, output='ba')
>>> sos = signal.ellip(13, 0.009, 80, 0.05, output='sos')
>>> x = signal.unit_impulse(700)
>>> y_tf = signal.lfilter(b, a, x)
>>> y_sos = signal.sosfilt(sos, x)
>>> plt.plot(y_tf, 'r', label='TF')
>>> plt.plot(y_sos, 'k', label='SOS')
>>> plt.legend(loc='best')
>>> plt.show()