scipy.signal.

bilinear#

scipy.signal.bilinear(b, a, fs=1.0)[source]#

通过双线性变换，从模拟传递函数计算数字IIR滤波器。

参数:

b类数组: 模拟传递函数分子多项式的系数，形式为复数或实数值的一维数组。
a类数组: 模拟传递函数分母多项式的系数，形式为复数或实数值的一维数组。
fs浮点数: 采样率，作为常规频率（例如，赫兹）。此函数中不进行预畸变。

返回:

betandarray: 数字传递函数分子多项式的系数，形式为复数或实数值的一维数组。
alphandarray: 数字传递函数分母多项式的系数，形式为复数或实数值的一维数组。

另请参见

lp2lp, lp2hp, lp2bp, lp2bs, bilinear_zpk

注意

参数 \(b = [b_0, \ldots, b_Q]\) 和 \(a = [a_0, \ldots, a_P]\) 是长度分别为 \(Q+1\) 和 \(P+1\) 的一维数组。它们定义了模拟传递函数

\[H_a(s) = \frac{b_0 s^Q + b_1 s^{Q-1} + \cdots + b_Q}{ a_0 s^P + a_1 s^{P-1} + \cdots + a_P}\ .\]

双线性变换 [1] 通过以下替换应用：

\[s = \kappa \frac{z-1}{z+1}\ , \qquad \kappa := 2 f_s\ ,\]

到 \(H_a(s)\) 中，其中 \(f_s\) 是采样率。这导致 \(z\) 域中的数字传递函数为

\[H_d(z) = \frac{b_0 \left(\kappa \frac{z-1}{z+1}\right)^Q + b_1 \left(\kappa \frac{z-1}{z+1}\right)^{Q-1} + \cdots + b_Q}{ a_0 \left(\kappa \frac{z-1}{z+1}\right)^P + a_1 \left(\kappa \frac{z-1}{z+1}\right)^{P-1} + \cdots + a_P}\ .\]

通过将分子和分母乘以 \((z+1)^N\) （其中 \(N=\max(P, Q)\)），可以简化此表达式。这使得 \(H_d(z)\) 可以重新表示为：

\[\begin{split}& & \frac{b_0 \big(\kappa (z-1)\big)^Q (z+1)^{N-Q} + b_1 \big(\kappa (z-1)\big)^{Q-1} (z+1)^{N-Q+1} + \cdots + b_Q(z+1)^N}{ a_0 \big(\kappa (z-1)\big)^P (z+1)^{N-P} + a_1 \big(\kappa (z-1)\big)^{P-1} (z+1)^{N-P+1} + \cdots + a_P(z+1)^N}\\ &=:& \frac{\beta_0 + \beta_1 z^{-1} + \cdots + \beta_N z^{-N}}{ \alpha_0 + \alpha_1 z^{-1} + \cdots + \alpha_N z^{-N}}\ .\end{split}\]

这是实现双线性变换的方程。请注意，对于大的 \(f_s\)，足够大的 \(P\) 或 \(Q\) 可能会导致 \(\kappa^Q\) 或 \(\kappa^P\) 发生数值溢出。

参考文献

[1] (1,2)

“双线性变换”，维基百科，https://en.wikipedia.org/wiki/Bilinear_transform

示例

以下示例展示了模拟带通滤波器的频率响应以及通过双线性变换导出的相应数字滤波器。

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np
...
>>> fs = 100  # sampling frequency
>>> om_c = 2 * np.pi * np.array([7, 13])  # corner frequencies
>>> bb_s, aa_s = signal.butter(4, om_c, btype='bandpass', analog=True, output='ba')
>>> bb_z, aa_z = signal.bilinear(bb_s, aa_s, fs)
...
>>> w_z, H_z = signal.freqz(bb_z, aa_z)  # frequency response of digitial filter
>>> w_s, H_s = signal.freqs(bb_s, aa_s, worN=w_z*fs)  # analog filter response
...
>>> f_z, f_s = w_z * fs / (2*np.pi), w_s / (2*np.pi)
>>> Hz_dB, Hs_dB = (20*np.log10(np.abs(H_).clip(1e-10)) for H_ in (H_z, H_s))
>>> fg0, ax0 = plt.subplots()
>>> ax0.set_title("Frequency Response of 4-th order Bandpass Filter")
>>> ax0.set(xlabel='Frequency $f$ in Hertz', ylabel='Magnitude in dB',
...         xlim=[f_z[1], fs/2], ylim=[-200, 2])
>>> ax0.semilogx(f_z, Hz_dB, alpha=.5, label=r'$|H_z(e^{j 2 \pi f})|$')
>>> ax0.semilogx(f_s, Hs_dB, alpha=.5, label=r'$|H_s(j 2 \pi f)|$')
>>> ax0.legend()
>>> ax0.grid(which='both', axis='x')
>>> ax0.grid(which='major', axis='y')
>>> plt.show()

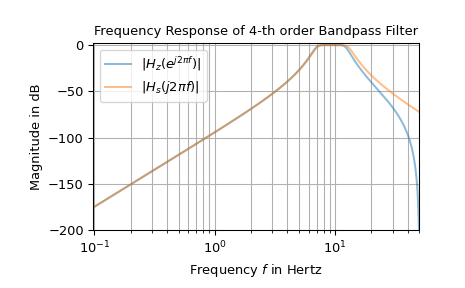
../../_images/scipy-signal-bilinear-1_00_00.png

图中所示高频部分的差异是由“频率畸变”效应引起的。[1] 描述了一种称为“预畸变”的方法来减少这些偏差。