平滑样条

一维样条平滑

对于插值问题，任务是构建一条通过给定数据集的曲线。如果数据有噪声，这可能不合适：我们希望构建一条平滑曲线 \(g(x)\)，它能近似输入数据而无需精确通过每个点。

为此，scipy.interpolate 允许构建平滑样条，它平衡了结果曲线 \(g(x)\) 与数据之间的接近程度以及 \(g(x)\) 的平滑度。数学上，任务是解决一个带惩罚项的最小二乘问题，其中惩罚项控制着 \(g(x)\) 的平滑度。

我们提供两种构建平滑样条的方法，它们在 (1) 惩罚项的形式和 (2) 构建平滑曲线的基础方面有所不同。下面我们考虑这两种方法。

前一种变体由 make_smoothing_spline 函数执行，它是 H. Woltring 经典 Fortran 包 gcvspl 的全新实现。后一种变体由 make_splrep 函数实现，它是 P. Dierckx 的 Fortran FITPACK 库的重新实现。FITPACK 库的旧版接口 也可用。

“经典”平滑样条和广义交叉验证 (GCV) 准则

给定数据数组 x 和 y 以及非负权重数组 w，我们寻找一个三次样条函数 g(x)，它最小化以下表达式：

\[\sum\limits_{j=1}^n w_j \left\lvert y_j - g(x_j) \right\rvert^2 + \lambda\int\limits_{x_1}^{x_n} \left( g^{(2)}(u) \right)^2 d u\]

其中 \(\lambda \geqslant 0\) 是一个非负惩罚参数，而 \(g^{(2)}(x)\) 是 \(g(x)\) 的二阶导数。第一项中的求和遍历数据点 \((x_j, y_j)\)，第二项中的积分在整个区间 \(x \in [x_1, x_n]\) 上进行。

这里第一项惩罚样条函数与数据之间的偏差，第二项惩罚二阶导数的较大值——这被视为曲线平滑度的准则。

目标函数 \(g(x)\) 被视为在数据点处具有节点的自然三次样条，最小化是在给定 \(\lambda\) 值下的样条系数上进行的。

显然，\(\lambda = 0\) 对应于插值问题——结果是自然插值样条；在相反的极限情况下，\(\lambda \gg 1\)，结果 \(g(x)\) 趋近于一条直线（因为最小化有效地将 \(g(x)\) 的二阶导数置零）。

平滑函数强烈依赖于 \(\lambda\)，并且可以选择“最优”惩罚值的多种策略。一种流行的策略是所谓的广义交叉验证 (GCV)：从概念上讲，这等同于比较在排除一个数据点的缩减数据集上构建的样条函数。直接应用这种“留一法”交叉验证过程非常昂贵，我们使用更高效的 GCV 算法。

为了在给定数据和惩罚参数的情况下构建平滑样条，我们使用函数 make_smoothing_spline。它的接口类似于插值样条的构造函数 make_interp_spline：它接受数据数组并返回一个可调用的 BSpline 实例。

此外，它接受一个可选的 lam 关键字参数来指定惩罚参数 \(\lambda\)。如果省略或设置为 None，则 \(\lambda\) 将通过 GCV 过程计算。

为了说明惩罚参数的效果，考虑一个带有噪声的正弦曲线的玩具示例

>>> import numpy as np
>>> from scipy.interpolate import make_smoothing_spline

生成一些有噪声的数据

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

为一系列惩罚参数值构造并绘制平滑样条

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> for lam in [0, 0.02, 10, None]:
...     spl = make_smoothing_spline(x, y, lam=lam)
...     plt.plot(xnew, spl(xnew), '-.', label=fr'$\lambda=${lam}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

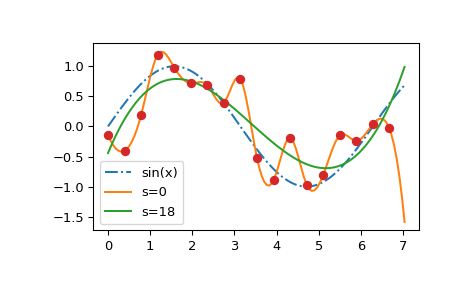
我们清楚地看到 lam=0 构造了插值样条；lam 的大值将结果曲线平坦化为一条直线；而 GCV 结果 lam=None 接近于底层正弦曲线。

y 数组的批处理

make_smoothing_spline 构造函数接受多维 y 数组和一个可选的 axis 参数，并以与插值样条构造函数 make_interp_spline 完全相同的方式解释它们。有关讨论和示例，请参阅插值部分。

自动节点选择的平滑样条

除了 make_smoothing_spline，SciPy 还提供了另一种形式，即 make_splrep 和 make_splprep 例程。前者构造样条函数，后者用于 \(d > 1\) 维的参数样条曲线。

虽然它们具有相似的 API（接收数据数组，返回 BSpline 实例），但它们与 make_smoothing_spline 在几个方面有所不同：

• 惩罚项的函数形式不同：这些例程使用 \(k\) 阶导数的跳跃而非 \((k-1)\) 阶导数的积分；

• 使用平滑参数 \(s\) 而非惩罚参数 \(\lambda\)；

• 这些例程自动构建节点向量；根据输入，生成的样条可能比数据点少得多。

• 默认边界条件不同：make_smoothing_spline 构造自然三次样条，而这些例程默认使用非节点边界条件。

让我们更详细地考虑该算法。首先，平滑准则。给定一个三次样条函数 \(g(x)\)，由节点 \(t_j\) 和系数 \(c_j\) 定义，考虑内部节点处三阶导数的跳跃，

\[D_j = g^{(3)}(t_j + 0) - g^{(3)}(t_j - 0) .\]

（对于 \(k\) 阶样条，我们本应使用 \(k\) 阶导数的跳跃。）

如果所有 \(D_j = 0\)，则 \(g(x)\) 是由节点跨越的整个域上的单个多项式。因此，我们将 \(g(x)\) 视为分段 \(C^2\) 可微样条函数，并将跳跃之和作为平滑准则，

\[\sum_j \left| D_j \right|^2 \to \mathrm{min} ,\]

其中最小化是在样条系数以及潜在的样条节点上进行的。

为了确保 \(g(x)\) 逼近输入数据 \(x_j\) 和 \(y_j\)，我们引入平滑参数 \(s \geqslant 0\) 并添加约束条件：

\[\sum_{j=1}^m \left[w_j \times \left(g(x_j) - y_j\right) \right]^2 \leqslant s .\]

在此公式中，平滑参数 \(s\) 是用户输入，很像经典平滑样条的惩罚参数 \(\lambda\)。

请注意，极限 s = 0 对应于插值问题，其中 \(g(x_j) = y_j\)。增加 s 会使拟合更平滑，而在 s 非常大的极限情况下，\(g(x)\) 退化为单个最佳拟合多项式。

对于固定的节点向量和给定的 \(s\) 值，最小化问题是线性的。如果我们也相对于节点进行最小化，问题就变为非线性。因此，我们需要指定一个迭代最小化过程来构建节点向量以及样条系数。

因此，我们使用以下程序：

• 我们从一个没有内部节点的样条开始，并检查用户提供的 \(s\) 值的平滑条件。如果满足，则完成。否则，

• 迭代，在每次迭代中我们

  • 通过分裂样条函数 \(g(x_j)\) 和数据 \(y_j\) 之间最大偏差的区间来添加新节点。

  • 构造 \(g(x)\) 的下一个近似值并检查平滑准则。

迭代停止，如果平滑条件满足，或者达到允许的最大节点数。后者可以由用户指定，或者采用默认值 len(x) + k + 1，这对应于对 x 数据数组进行 k 次样条插值。

重新表述并略过细节，该过程是迭代遍历由 generate_knots 生成的节点向量，并在每一步应用 make_lsq_spline。在伪代码中：

for t in generate_knots(x, y, s=s):
    g = make_lsq_spline(x, y, t=t)     # construct
    if ((y - g(x))**2).sum() < s:      # check smoothness
        break

注意

对于 s=0，我们采取捷径，构造具有非节点边界条件的插值样条，而不是迭代。

构建节点向量的迭代过程通过生成器函数 generate_knots 提供。例如：

>>> import numpy as np
>>> from scipy.interpolate import generate_knots
>>> x = np.arange(7)
>>> y = x**4
>>> list(generate_knots(x, y, s=1))   # default is cubic splines, k=3
[array([0., 0., 0., 0., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 3., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 3., 5., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.])]

对于 s=0，生成器会截断

>>> list(generate_knots(x, y, s=0))
[array([0, 0, 0, 0, 2, 3, 4, 6, 6, 6, 6])]

注意

一般来说，节点位于数据点处。例外情况是偶数阶样条，其中节点可以放置在远离数据的地方。这发生在 s=0（插值）时，或当 s 足够小以致达到最大节点数，例程切换到 s=0 节点向量（有时称为 Greville 绝对值）。

>>> list(generate_knots(x, y, s=1, k=2))   # k=2, quadratic spline
[array([0., 0., 0., 6., 6., 6.]),
 array([0., 0., 0., 3., 6., 6., 6.]),
 array([0., 0., 0., 3., 5., 6., 6., 6.]),
 array([0., 0., 0., 2., 3., 5., 6., 6., 6.]),
 array([0. , 0. , 0. , 1.5, 2.5, 3.5, 4.5, 6. , 6. , 6. ])]   # Greville sites

注意

构建节点向量的启发式方法遵循 FITPACK Fortran 库使用的算法。算法是相同的，由于浮点舍入可能会有微小差异。

我们现在使用与前一节相同的玩具数据集来演示 make_splrep 的结果：

>>> import numpy as np
>>> from scipy.interpolate import make_splrep

生成一些有噪声的数据

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

构造并绘制一系列 s 参数值的平滑样条

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi

>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, make_splrep(x, y, s=0)(xnew), '-', label='s=0')
>>> plt.plot(xnew, make_splrep(x, y, s=len(x))(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

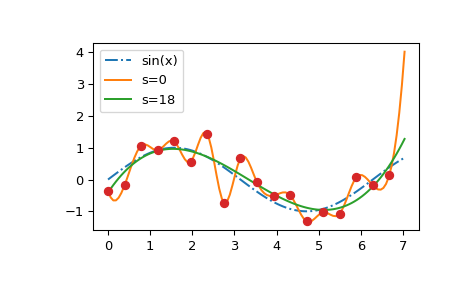
我们看到 \(s=0\) 曲线遵循数据点的（随机）波动，而 \(s > 0\) 曲线接近底层正弦函数。另请注意，外推值随 \(s\) 的值而剧烈变化。

找到一个好的 \(s\) 值是一个试错过程。如果权重对应于输入数据的标准差的倒数，则预期“好”的 \(s\) 值介于 \(m - \sqrt{2m}\) 和 \(m + \sqrt{2m}\) 之间，其中 \(m\) 是数据点的数量。如果所有权重都等于 1，一个合理的选择可能是 \(s \sim m\,\sigma^2\)，其中 \(\sigma\) 是数据标准差的估计值。

注意

节点的数量非常强烈地依赖于 s。 s 的微小变化可能导致节点数量的剧烈变化。

注意

make_smoothing_spline 和 make_splrep 都允许加权拟合，其中用户提供一个权重数组 w。请注意，定义有所不同：make_smoothing_spline 会对权重进行平方以与 gcvspl 保持一致，而 make_splrep 不会——以与 FITPACK 保持一致。

\(d>1\) 维平滑样条曲线

到目前为止，我们已经考虑了在给定数据数组 x 和 y 的情况下构建平滑样条函数 \(g(x)\)。现在我们考虑一个相关的问题，即构建一个平滑样条曲线，我们将数据视为平面上的点 \(\mathbf{p}_j = (x_j, y_j)\)，并且我们希望构建一个参数函数 \(\mathbf{g}(\mathbf{p}) = (g_x(u), g_y(u))\)，其中参数 \(u_j\) 的值对应于 \(x_j\) 和 \(y_j\)。

请注意，此问题很容易推广到更高维度，\(d > 2\)：我们只需有 \(d\) 个数据数组并构造一个具有 \(d\) 个分量的参数函数。

另请注意，参数化的选择不能自动化，即使对于插值曲线，不同的参数化也可能导致相同数据的曲线非常不同。

一旦选择了特定的参数化形式，构建平滑曲线的问题在概念上与构建平滑样条函数非常相似。简而言之，

• 样条节点是从参数 \(u\) 的值添加的，并且

• 我们为样条函数考虑的最小化成本函数和约束条件都只是在 \(d\) 个分量上增加了一个求和。

函数 make_splrep 的“参数化”泛化是 make_splprep，其文档字符串详细阐述了它所解决的最小化问题的精确数学公式。

参数化情况的主要用户可见差异是用户界面：

• make_splprep 不接受两个数据数组 x 和 y，而是接收一个二维数组，其中第二维的大小为 \(d\)，并且每个数据数组都沿着第一维存储（或者，您可以提供一个一维数组列表）。

• 返回值是一个对：一个 BSpline 实例和对应于输入数据数组的参数值数组 u。

默认情况下，make_splprep 构造并返回输入数据的弦长参数化（有关详细信息，请参阅参数样条曲线部分）。或者，您可以提供自己的参数值数组 u。

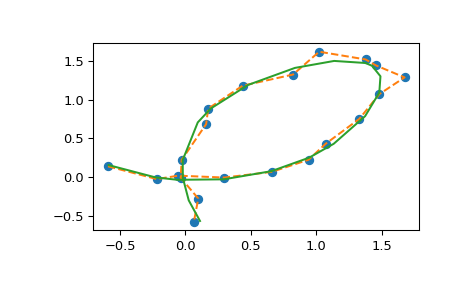
为了说明 API，考虑一个玩具问题：我们有一些从笛卡尔叶形线采样的数据加上一些噪声。

>>> import numpy as np
>>> from scipy.interpolate import make_splprep
>>> th = np.linspace(-0.2, np.pi/2 + 0.2, 21)
>>> r = 3 * np.sin(th) * np.cos(th) / (np.sin(th)**3 + np.cos(th)**3)
>>> x, y = r * np.cos(th), r * np.sin(th)

添加一些噪声并构造插值器

>>> rng = np.random.default_rng()
>>> xn = x + 0.1*rng.uniform(-1, 1, size=len(x))
>>> yn = y + 0.1*rng.uniform(-1, 1, size=len(x))
>>> spl, u = make_splprep([xn, yn], s=0)   # note the [xn, yn] argument
>>> spl_n, u_n = make_splprep([xn, yn], s=0.1)

并绘制结果（spl(u) 的结果是一个二维数组，因此我们将其解包为一对 x 和 y 数组用于绘图）。

>>> import matplotlib.pyplot as plt
>>> plt.plot(xn, yn, 'o')
>>> plt.plot(*spl(u), '--')
>>> plt.plot(*spl_n(u_n), '-')
>>> plt.show()

y 数组的批处理

与插值样条和GCV 平滑器不同，make_splrep 和 make_splprep 不允许多维 y 数组，并要求 x.ndim == y.ndim == 1。

此限制的技术原因在于节点向量 t 的长度取决于 y 值，因此对于批处理的 y，批处理的 t 可能是一个不规则数组，而 BSpline 无法处理。

因此，如果您需要处理批处理输入，您需要手动循环批处理并为批处理的每个切片构造一个 BSpline 对象。完成此操作后，您可以通过以下方式模仿 BSpline 的评估行为：

class BatchSpline:
    """BSpline-like class with batch behavior."""
    def __init__(self, x, y, axis, *, spline, **kwargs):
        y = np.moveaxis(y, axis, -1)
        self._batch_shape = y.shape[:-1]
        self._splines = [
            spline(x, yi, **kwargs) for yi in y.reshape(-1, y.shape[-1])
        ]
        self._axis = axis

    def __call__(self, x):
        y = [spline(x) for spline in self._splines]
        y = np.reshape(y, self._batch_shape + x.shape)
        return np.moveaxis(y, -1, self._axis) if x.shape else y

一维样条平滑的旧例程

除了我们前面讨论的平滑样条构造函数，scipy.interpolate 还提供了对 P. Dierckx 编写的古老的 FITPACK Fortran 库中例程的直接接口。

注意

这些接口应被视为旧版——虽然我们不打算弃用或移除它们，但我们建议新代码使用更现代的替代方案：make_smoothing_spline、make_splrep 或 make_splprep。

由于历史原因，scipy.interpolate 为 FITPACK 提供了两个等价的接口：一个函数式接口和一个面向对象接口。虽然等价，但这些接口有不同的默认值。下面我们依次讨论它们，从函数式接口开始。

过程式接口 (splrep)

样条插值需要两个基本步骤：(1) 计算曲线的样条表示，以及 (2) 在所需点评估样条。为了找到样条表示，有两种不同的方式来表示曲线并获得（平滑）样条系数：直接法和参数法。直接法使用函数 splrep 找到二维平面中曲线的样条表示。前两个参数是唯一必需的，它们提供了曲线的 \(x\) 和 \(y\) 分量。正常输出是一个 3 元组 \(\left(t,c,k\right)\)，包含节点 \(t\)、系数 \(c\) 和样条的阶数 \(k\)。默认样条阶数是三次，但这可以通过输入关键字 k 更改。

节点数组将插值区间定义为 t[k:-k]，因此 t 数组的前 \(k+1\) 个和最后 \(k+1\) 个条目定义了边界节点。系数是一个一维数组，长度至少为 len(t) - k - 1。有些例程会将此数组填充至 len(c) == len(t)——这些额外的系数在样条评估时会被忽略。

tck 元组格式与插值 b 样条兼容：splrep 的输出可以封装到 BSpline 对象中，例如 BSpline(*tck)，并且下面描述的评估/积分/求根例程可以互换使用 tck 元组和 BSpline 对象。

对于N维空间中的曲线，函数 splprep 允许以参数形式定义曲线。对于此函数，只需要1个输入参数。此输入是表示N维空间中曲线的 \(N\) 个数组的列表。每个数组的长度是曲线点的数量，每个数组提供N维数据点的一个分量。参数变量通过关键字参数 u 给出，默认为 \(0\) 到 \(1\) 之间等间距的单调序列（即均匀参数化）。

输出包含两个对象：一个 3 元组 \(\left(t,c,k\right)\)，包含样条表示和参数变量 \(u.\)

系数是一个包含 \(N\) 个数组的列表，其中每个数组对应于输入数据的一个维度。请注意，节点 t 对应于曲线 u 的参数化。

关键字参数 s 用于指定样条拟合期间要执行的平滑量。 \(s\) 的默认值为 \(s=m-\sqrt{2m}\)，其中 \(m\) 是要拟合的数据点数。因此，如果不需要平滑，则应将 \(\mathbf{s}=0\) 传递给例程。

一旦确定了数据的样条表示，可以使用 splev 函数或将 tck 元组包装成 BSpline 对象进行评估，如下所示。

我们首先说明 s 参数对平滑一些合成噪声数据的影响

>>> import numpy as np
>>> from scipy.interpolate import splrep, BSpline

生成一些有噪声的数据

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

构造两个 s 值不同的样条。

>>> tck = splrep(x, y, s=0)
>>> tck_s = splrep(x, y, s=len(x))

并绘制它们

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, BSpline(*tck)(xnew), '-', label='s=0')
>>> plt.plot(xnew, BSpline(*tck_s)(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

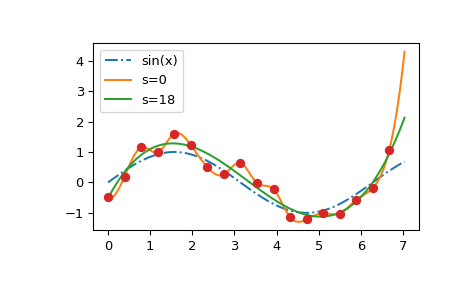
我们看到 s=0 曲线遵循数据点的（随机）波动，而 s > 0 曲线接近底层正弦函数。另请注意，外推值随 s 的值而剧烈变化。

s 的默认值取决于是否提供了权重，并且对于 splrep 和 splprep 也不同。因此，我们建议始终明确提供 s 的值。

操作样条对象：过程式 (splXXX)

一旦确定了数据的样条表示，就可以使用函数来评估样条（splev）及其导数（splev, spalde），以及在任意两点之间样条的积分（splint）。此外，对于具有8个或更多节点的三次样条（\(k=3\)），可以估计样条的根（sproot）。这些函数将在下面的示例中演示。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate

三次样条

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = interpolate.splev(xnew, tck, der=0)

请注意，最后一行等同于 BSpline(*tck)(xnew)。

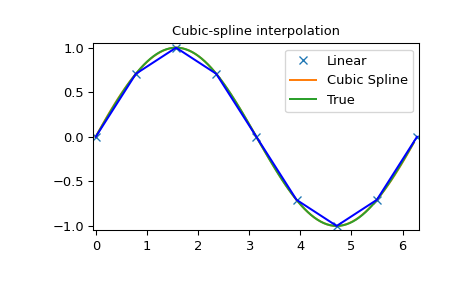
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Cubic-spline interpolation')
>>> plt.show()

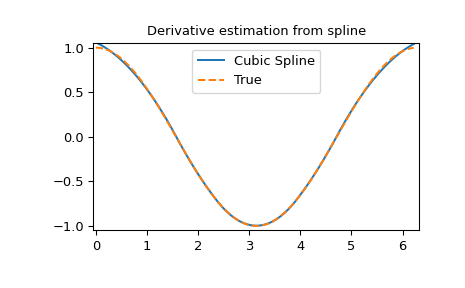
样条的导数

>>> yder = interpolate.splev(xnew, tck, der=1)   # or BSpline(*tck)(xnew, 1)
>>> plt.figure()
>>> plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Derivative estimation from spline')
>>> plt.show()

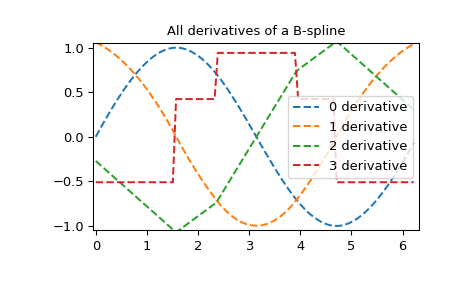
样条的所有导数

>>> yders = interpolate.spalde(xnew, tck)
>>> plt.figure()
>>> for i in range(len(yders[0])):
...    plt.plot(xnew, [d[i] for d in yders], '--', label=f"{i} derivative")
>>> plt.legend()
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('All derivatives of a B-spline')
>>> plt.show()

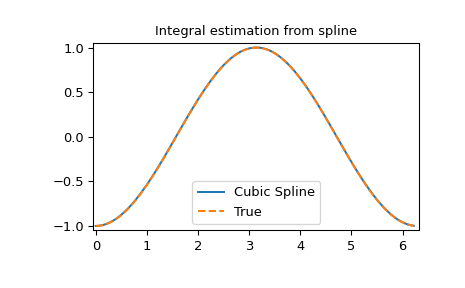
样条的积分

>>> def integ(x, tck, constant=-1):
...     x = np.atleast_1d(x)
...     out = np.zeros(x.shape, dtype=x.dtype)
...     for n in range(len(out)):
...         out[n] = interpolate.splint(0, x[n], tck)
...     out += constant
...     return out

>>> yint = integ(xnew, tck)
>>> plt.figure()
>>> plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Integral estimation from spline')
>>> plt.show()

样条的根

>>> interpolate.sproot(tck)
array([3.1416])  # may vary

请注意，sproot 可能无法在近似区间的边缘 \(x = 0\) 处找到明显的解。如果我们将样条定义在一个稍大的区间上，我们就能找到两个根 \(x = 0\) 和 \(x = \pi\)

>>> x = np.linspace(-np.pi/4, np.pi + np.pi/4, 51)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> interpolate.sproot(tck)
array([0., 3.1416])

参数样条

>>> t = np.arange(0, 1.1, .1)
>>> x = np.sin(2*np.pi*t)
>>> y = np.cos(2*np.pi*t)
>>> tck, u = interpolate.splprep([x, y], s=0)
>>> unew = np.arange(0, 1.01, 0.01)
>>> out = interpolate.splev(unew, tck)
>>> plt.figure()
>>> plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-1.05, 1.05, -1.05, 1.05])
>>> plt.title('Spline of parametrically-defined curve')
>>> plt.show()

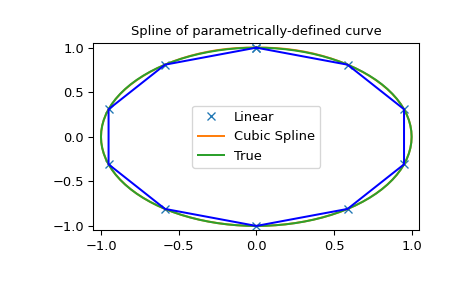
请注意，在最后一个示例中，splprep 将样条系数作为数组列表返回，其中每个数组对应于输入数据的一个维度。因此，要将其输出封装到 BSpline 中，我们需要转置系数（或使用 BSpline(..., axis=1)）

>>> tt, cc, k = tck
>>> cc = np.array(cc)
>>> bspl = BSpline(tt, cc.T, k)    # note the transpose
>>> xy = bspl(u)
>>> xx, yy = xy.T   # transpose to unpack into a pair of arrays
>>> np.allclose(x, xx)
True
>>> np.allclose(y, yy)
True

面向对象 (UnivariateSpline)

上述样条拟合功能也可通过面向对象的接口获得。一维样条是 UnivariateSpline 类的对象，并通过向构造函数提供曲线的 \(x\) 和 \(y\) 分量作为参数来创建。该类定义了 __call__，允许使用 x 轴值调用对象，样条应在这些值处进行评估，并返回插值的 y 值。这在下面的子类 InterpolatedUnivariateSpline 示例中有所展示。integral、derivatives 和 roots 方法也适用于 UnivariateSpline 对象，允许计算样条的定积分、导数和根。

UnivariateSpline 类还可以通过提供非零的平滑参数 s 来平滑数据，其含义与上述 splrep 函数的 s 关键字相同。这导致样条的节点数少于数据点数，因此不再严格是插值样条，而是平滑样条。如果不需要此功能，则可以使用 InterpolatedUnivariateSpline 类。它是 UnivariateSpline 的子类，它始终通过所有点（相当于强制平滑参数为 0）。此类别在下面的示例中演示。

LSQUnivariateSpline 类是 UnivariateSpline 的另一个子类。它允许用户使用参数 t 明确指定内部节点的数量和位置。这允许创建具有非线性间距的自定义样条，以在某些域中进行插值并在其他域中进行平滑，或改变样条的特性。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate

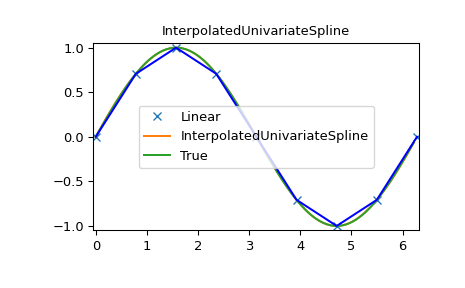
插值一元样条（InterpolatedUnivariateSpline）

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> s = interpolate.InterpolatedUnivariateSpline(x, y)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = s(xnew)

>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('InterpolatedUnivariateSpline')
>>> plt.show()

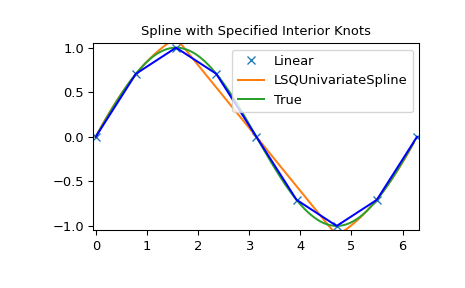
具有非均匀节点的LSQUnivarateSpline

>>> t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
>>> s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
>>> ynew = s(xnew)

>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Spline with Specified Interior Knots')
>>> plt.show()

二维平滑样条

除了平滑一维样条，FITPACK 库还提供了将二维曲面拟合到二维数据的方法。这些曲面可以被认为是两个参数的函数，\(z = g(x, y)\)，构造为一维样条的张量积。

假设数据保存在三个数组中：x、y 和 z，这些数据数组可以有两种解释方式。首先——散点插值问题——数据被假定为成对的，即值对 x[i] 和 y[i] 代表点 i 的坐标，该点对应于 z[i]。

构造曲面 \(g(x, y)\) 以满足

\[\sum_i \left[ w_i (g(x_i, y_i) - z_i)\right]^2 \leqslant s\]

其中 \(w_i\) 是非负权重，s 是输入参数，称为平滑因子，它控制结果函数 g(x, y) 的平滑度与数据近似质量（即 \(g(x_i, y_i)\) 和 \(z_i\) 之间的差异）之间的相互作用。\(s = 0\) 的极限形式上对应于插值，其中曲面穿过输入数据，\(g(x_i, y_i) = z_i\)。但是，请参阅下面的注释。

第二种情况——矩形网格插值问题——是指数据点被假定位于由 x 和 y 数组元素的所有对定义的矩形网格上。对于此问题，z 数组被假定为二维，z[i, j] 对应于 (x[i], y[j])。双变量样条函数 \(g(x, y)\) 被构造为满足

\[\sum_i \sum_j \left[ (g(x_i, y_j) - z_{i,j})\right]^2 \leqslant s\]

其中 s 是平滑因子。这里 \(s=0\) 的极限也形式上对应于插值，即 \(g(x_i, y_j) = z_{i, j}\)。

注意

在内部，平滑曲面 \(g(x, y)\) 是通过将样条节点放置在由数据数组定义的边界框中来构造的。节点通过 FITPACK 算法自动放置，直到达到所需的平滑度。

节点可以放置在远离数据点的地方。

虽然 \(s=0\) 形式上对应于双变量样条插值，但 FITPACK 算法并非为插值而设计，可能会导致意想不到的结果。

对于散点数据插值，首选 griddata；对于规则网格上的数据，首选 RegularGridInterpolator。

注意

如果输入数据 x 和 y 的输入维度不相称且相差多个数量级，则插值函数 \(g(x, y)\) 可能会出现数值伪影。请考虑在插值之前重新缩放数据。

我们现在依次考虑这两个样条拟合问题。

散点数据的双变量样条拟合

底层 FITPACK 库有两个接口：过程式接口和面向对象接口。

过程式接口 (`bisplrep`)

为了将（平滑）样条拟合到二维曲面，可以使用函数 bisplrep。此函数将一维数组 x、y 和 z 作为必需输入，这些数组表示曲面 \(z=f(x, y)\) 上的点。在 x 和 y 方向上的样条阶数可以通过可选参数 kx 和 ky 指定。默认是双三次样条，kx=ky=3。

bisplrep 的输出是一个列表 [tx ,ty, c, kx, ky]，其条目分别表示节点位置的分量、样条的系数以及样条在每个坐标中的阶数。将此列表保存在单个对象 tck 中很方便，这样可以轻松传递给函数 bisplev。关键字 s 可用于更改在确定适当样条时对数据执行的平滑量。 \(s\) 的推荐值取决于权重 \(w_i\)。如果这些权重取为 \(1/d_i\)，其中 \(d_i\) 是 \(z_i\) 标准差的估计值，则 \(s\) 的一个好值应在 \(m- \sqrt{2m}, m + \sqrt{2m}\) 范围内，其中 \(m\) 是 x、y 和 z 向量中的数据点数。

默认值为 \(s=m-\sqrt{2m}\)。因此，如果不需要平滑，则应将 s=0 传递给 `bisplrep`。（但是请参见上面的注释）。

要评估二维样条及其偏导数（直至样条的阶数），需要函数 bisplev。此函数将两个一维数组作为前两个参数，其叉积指定了评估样条的域。第三个参数是 bisplrep 返回的 tck 列表。如果需要，第四和第五个参数分别提供在 \(x\) 和 \(y\) 方向上的偏导数阶数。

注意

重要的是要注意，二维插值不应用于查找图像的样条表示。所使用的算法不适用于大量的输入点。scipy.signal 和 scipy.ndimage 包含更合适的算法来查找图像的样条表示。

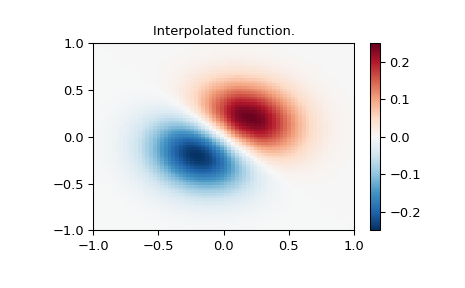
二维插值命令旨在用于插值二维函数，如下例所示。此示例使用 NumPy 中的 mgrid 命令，该命令对于在多个维度中定义“网格”非常有用。（如果不需要完整的网格，另请参阅 ogrid 命令）。输出参数的数量和每个参数的维度由传递给 mgrid 的索引对象的数量决定。

>>> import numpy as np
>>> from scipy import interpolate
>>> import matplotlib.pyplot as plt

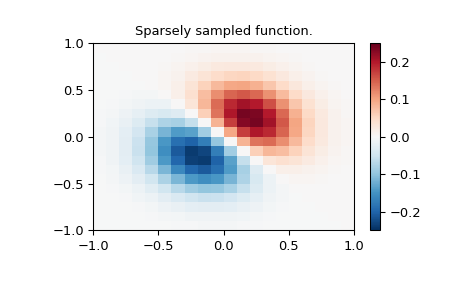
在稀疏的 20x20 网格上定义函数

>>> x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
>>> x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
>>> y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
>>> z = (x+y) * np.exp(-6.0*(x*x+y*y))

>>> plt.figure()
>>> lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
>>> plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Sparsely sampled function.")
>>> plt.show()

在新的 70x70 网格上插值函数

>>> xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
>>> xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
>>> ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
>>> tck = interpolate.bisplrep(x, y, z, s=0)
>>> znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)

>>> plt.figure()
>>> plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Interpolated function.")
>>> plt.show()

面向对象接口 (`SmoothBivariateSpline`)

用于散点数据双变量样条平滑的面向对象接口，即 SmoothBivariateSpline 类，实现了 bisplrep / bisplev 对功能的一个子集，并且具有不同的默认值。

它将权重数组的元素设为单位，即 \(w_i = 1\)，并在给定平滑因子 s 的输入值的情况下自动构造节点向量——默认值为 \(m\)，即数据点的数量。

样条在 x 和 y 方向上的阶数由可选参数 kx 和 ky 控制，默认值为 kx=ky=3。

我们通过以下示例来说明平滑因子效应：

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import SmoothBivariateSpline

import warnings
warnings.simplefilter('ignore')

train_x, train_y = np.meshgrid(np.arange(-5, 5, 0.5), np.arange(-5, 5, 0.5))
train_x = train_x.flatten()
train_y = train_y.flatten()

def z_func(x, y):
    return np.cos(x) + np.sin(y) ** 2 + 0.05 * x + 0.1 * y

train_z = z_func(train_x, train_y)
interp_func = SmoothBivariateSpline(train_x, train_y, train_z, s=0.0)
smth_func = SmoothBivariateSpline(train_x, train_y, train_z)

test_x = np.arange(-9, 9, 0.01)
test_y = np.arange(-9, 9, 0.01)
grid_x, grid_y = np.meshgrid(test_x, test_y)

interp_result = interp_func(test_x, test_y).T
smth_result = smth_func(test_x, test_y).T
perfect_result = z_func(grid_x, grid_y)

fig, axes = plt.subplots(1, 3, figsize=(16, 8))
extent = [test_x[0], test_x[-1], test_y[0], test_y[-1]]
opts = dict(aspect='equal', cmap='nipy_spectral', extent=extent, vmin=-1.5, vmax=2.5)

im = axes[0].imshow(perfect_result, **opts)
fig.colorbar(im, ax=axes[0], orientation='horizontal')
axes[0].plot(train_x, train_y, 'w.')
axes[0].set_title('Perfect result, sampled function', fontsize=21)

im = axes[1].imshow(smth_result, **opts)
axes[1].plot(train_x, train_y, 'w.')
fig.colorbar(im, ax=axes[1], orientation='horizontal')
axes[1].set_title('s=default', fontsize=21)

im = axes[2].imshow(interp_result, **opts)
fig.colorbar(im, ax=axes[2], orientation='horizontal')
axes[2].plot(train_x, train_y, 'w.')
axes[2].set_title('s=0', fontsize=21)

plt.tight_layout()
plt.show()

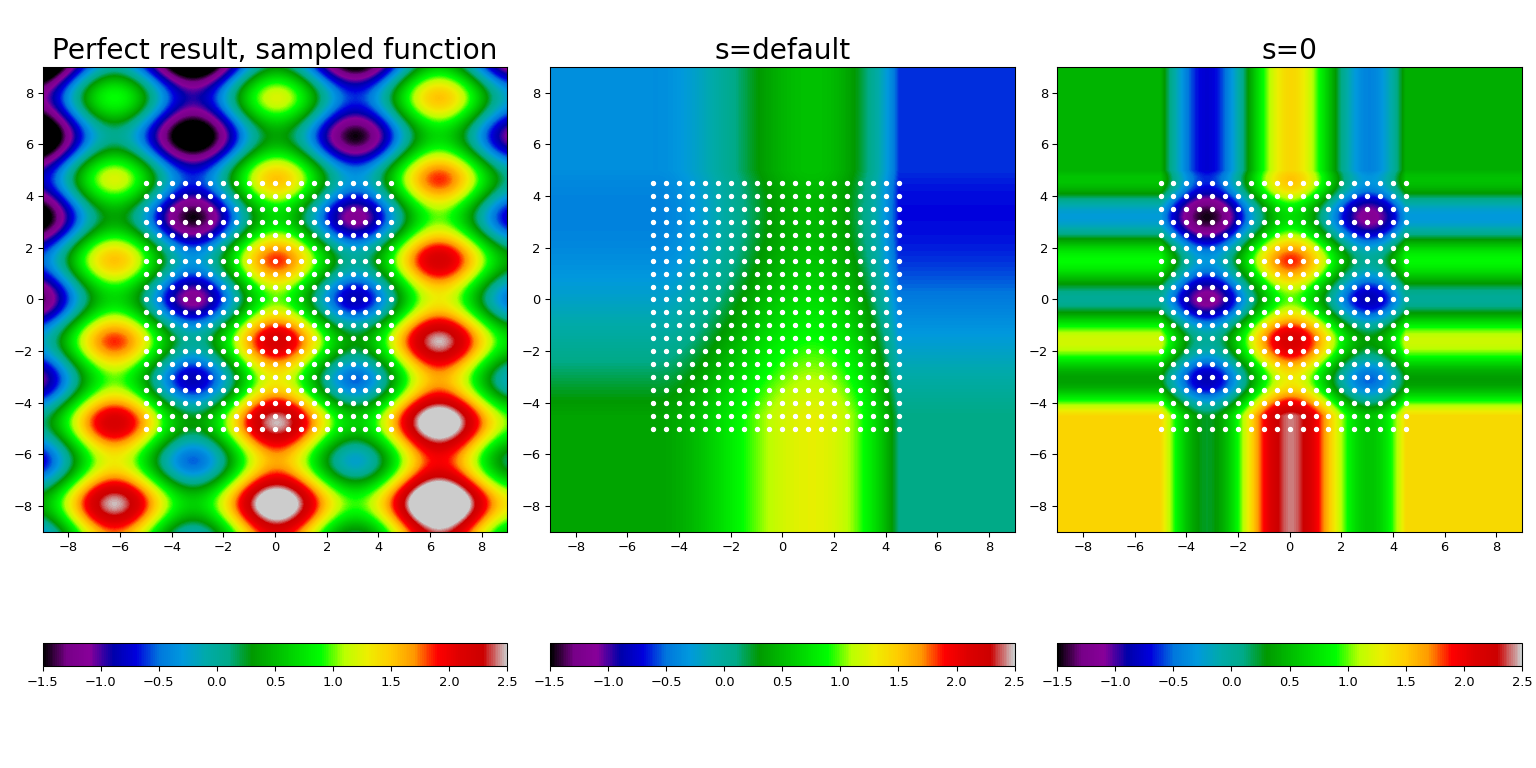
这里我们取一个已知函数（在最左侧面板中显示），在网格点上采样（由白点显示），然后使用默认平滑（中心面板）和强制插值（最右侧面板）构造样条拟合。

几个特征清晰可见。首先，s 的默认值对于此数据提供了过多的平滑；强制插值条件，即 s = 0，可以以合理的精度恢复底层函数。其次，在插值范围之外（即白色点覆盖的区域）使用最近邻常数进行外推。最后，我们不得不压制警告（是的，这是一个坏习惯！）。

这里在 s=0 情况下发出了警告，表示当强制插值条件时，FITPACK 遇到了内部困难。如果您在代码中看到此警告，请考虑切换到 bisplrep 并增加其 nxest、nyest 参数（有关更多详细信息，请参阅 bisplrep 文档字符串）。

网格数据双变量样条拟合

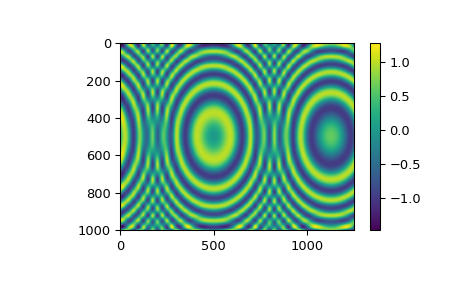
对于网格化的二维数据，可以使用 RectBivariateSpline 类进行平滑张量积样条拟合。它的接口类似于 SmoothBivariateSpline，主要区别在于一维输入数组 x 和 y 被理解为定义二维网格（作为它们的外积），而 z 数组是二维的，形状为 len(x) 乘以 len(y)。

样条在 x 和 y 方向上的阶数由可选参数 kx 和 ky 控制，默认值为 kx=ky=3，即双三次样条。

平滑因子的默认值为 s=0。尽管如此，我们仍建议始终明确指定 s。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline

x = np.arange(-5.01, 5.01, 0.25)        # the grid is an outer product
y = np.arange(-5.01, 7.51, 0.25)        # of x and y arrays

xx, yy = np.meshgrid(x, y, indexing='ij')
z = np.sin(xx**2 + 2.*yy**2)            # z array needs to be 2-D

func = RectBivariateSpline(x, y, z, s=0)

xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 7.51, 1e-2)
znew = func(xnew, ynew)

plt.imshow(znew)
plt.colorbar()
plt.show()

球坐标数据双变量样条拟合

如果您的数据以球坐标 \(r = r(\theta, \phi)\) 给出，SmoothSphereBivariateSpline 和 RectSphereBivariateSpline 分别提供了 SmoothBivariateSpline 和 RectBivariateSpline 的便捷对应物。

这些类确保了样条拟合在 \(\theta \in [0, \pi]\) 和 \(\phi \in [0, 2\pi]\) 上的周期性，并对极点的连续性提供了一些控制。有关详细信息，请参阅这些类的文档字符串。