scipy.interpolate.

SmoothSphereBivariateSpline

class scipy.interpolate.SmoothSphereBivariateSpline(theta, phi, r, w=None, s=0.0, eps=1e-16)

球面坐标系中的光滑二元样条逼近。

0.11.0 版本新增。

参数:

theta, phi, rarray_like

一维数据点序列（顺序不重要）。坐标必须以弧度给出。Theta 必须在 [0, pi] 区间内，phi 必须在 [0, 2pi] 区间内。

warray_like, 可选

正一维权重序列。

sfloat, 可选

用于估计条件的平滑因子，定义为： sum((w(i)*(r(i) - s(theta(i), phi(i))))**2, axis=0) <= s 默认值为 s=len(w)，如果 1/w[i] 是 r[i] 标准差的估计值，则此值应为良好值。

epsfloat, 可选

用于确定超定线性方程组有效秩的阈值。eps 的值应在开区间 (0, 1) 内，默认值为 1e-16。

方法

__call__(theta, phi[, dtheta, dphi, grid])	在给定位置评估样条函数或其导数。
ev(theta, phi[, dtheta, dphi])	在点处评估样条函数
get_coeffs()	返回样条系数。
get_knots()	返回一个元组 (tx,ty)，其中 tx,ty 分别包含样条函数在 x、y 变量上的结位置。
get_residual()	返回样条逼近的加权平方残差和： sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0)
partial_derivative(dx, dy)	构造一个表示此样条函数的偏导数的新样条函数。

另请参阅

BivariateSpline

二元样条的基类。

UnivariateSpline

用于拟合给定数据点的光滑一元样条函数。

SmoothBivariateSpline

通过给定点的平滑二元样条函数

LSQBivariateSpline

使用加权最小二乘拟合的二元样条函数

RectSphereBivariateSpline

球面上矩形网格上的二元样条函数

LSQSphereBivariateSpline

使用加权最小二乘拟合的球面坐标系中的二元样条函数

RectBivariateSpline

矩形网格上的二元样条函数。

bisplrep

一个查找曲面二元 B 样条表示的函数

bisplev

一个评估二元 B 样条函数及其导数的函数

备注

更多信息，请参阅 FITPACK 网站上关于此函数的内容。

示例

在浏览器中尝试！

假设我们有一个粗略网格上的全局数据（输入数据不必在网格上）

>>> import numpy as np
>>> theta = np.linspace(0., np.pi, 7)
>>> phi = np.linspace(0., 2*np.pi, 9)
>>> data = np.empty((theta.shape[0], phi.shape[0]))
>>> data[:,0], data[0,:], data[-1,:] = 0., 0., 0.
>>> data[1:-1,1], data[1:-1,-1] = 1., 1.
>>> data[1,1:-1], data[-2,1:-1] = 1., 1.
>>> data[2:-2,2], data[2:-2,-2] = 2., 2.
>>> data[2,2:-2], data[-3,2:-2] = 2., 2.
>>> data[3,3:-2] = 3.
>>> data = np.roll(data, 4, 1)

我们需要设置插值器对象

>>> lats, lons = np.meshgrid(theta, phi)
>>> from scipy.interpolate import SmoothSphereBivariateSpline
>>> lut = SmoothSphereBivariateSpline(lats.ravel(), lons.ravel(),
...                                   data.T.ravel(), s=3.5)

作为第一个测试，我们将看看该算法在输入坐标上运行时返回什么

>>> data_orig = lut(theta, phi)

最后，我们将数据插值到更精细的网格

>>> fine_lats = np.linspace(0., np.pi, 70)
>>> fine_lons = np.linspace(0., 2 * np.pi, 90)

>>> data_smth = lut(fine_lats, fine_lons)

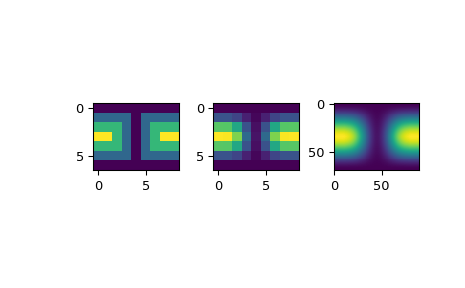
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(131)
>>> ax1.imshow(data, interpolation='nearest')
>>> ax2 = fig.add_subplot(132)
>>> ax2.imshow(data_orig, interpolation='nearest')
>>> ax3 = fig.add_subplot(133)
>>> ax3.imshow(data_smth, interpolation='nearest')
>>> plt.show()

返回在新标签页中打开