scipy.interpolate.

RegularGridInterpolator#

class scipy.interpolate.RegularGridInterpolator(points, values, method='linear', bounds_error=True, fill_value=nan, *, solver=None, solver_args=None)[source]#

N ≥ 1 维直角网格上的指定阶插值器。

数据必须定义在直角网格上；也就是说，一个间距均匀或不均匀的矩形网格。支持线性插值、最近邻插值、样条插值。设置插值器对象后，每次评估时都可以选择插值方法。

参数:

pointsndarray 浮点数的元组，形状为 (m1, ), …, (mn, ): 定义 N 维直角网格的点。每个维度中的点（即 points 元组的每个元素）必须严格递增或递减。
values类数组，形状为 (m1, …, mn, …): N 维直角网格上的数据。接受复数数据。
methodstr, 可选: 要执行的插值方法。支持“linear”、“nearest”、“slinear”、“cubic”、“quintic”和“pchip”。此参数将成为对象 __call__ 方法的默认值。默认为“linear”。
bounds_errorbool, 可选: 如果为 True，当请求插值值超出输入数据域时，将引发 ValueError。如果为 False，则使用 fill_value。默认为 True。
fill_value浮点数或 None, 可选: 用于插值域外点的值。如果为 None，则域外值将进行外推。默认为 np.nan。
solver可调用对象，可选: 仅用于方法“slinear”、“cubic”和“quintic”。用于构建 NdBSpline 实例的稀疏线性代数求解器。默认为迭代求解器 scipy.sparse.linalg.gcrotmk。

版本 1.13 新增。
solver_args: dict, 可选: 要传递给 solver 的其他参数（如果有）。

版本 1.13 新增。

属性:

gridndarray 元组: 定义 N 维直角网格的点。此元组通过 np.meshgrid(*grid, indexing='ij') 定义完整网格
valuesndarray: 网格上的数据值。
methodstr: 插值方法。
fill_value浮点数或 None: 将此值用于 __call__ 的越界参数。
bounds_errorbool: 如果为 True，越界参数将引发 ValueError。

方法

__call__(xi[, method, nu])

坐标插值。

另请参见

NearestNDInterpolator: N 维非结构化数据上的最近邻插值器
LinearNDInterpolator: N 维非结构化数据上的分段线性插值器
interpn: 一个封装 RegularGridInterpolator 的便捷函数
scipy.ndimage.map_coordinates: 等间距网格上的插值（适用于例如 N 维图像重采样）

注意事项

与 LinearNDInterpolator 和 NearestNDInterpolator 不同，此类通过利用规则网格结构避免了输入数据的昂贵三角剖分。

换句话说，此类假定数据定义在直角网格上。

版本 0.14 新增。

“slinear”(k=1)、“cubic”(k=3) 和“quintic”(k=5) 方法是张量积样条插值器，其中 k 是样条的次数。如果任何维度的点数少于 k + 1，将引发错误。

版本 1.9 新增。

如果输入数据维度单位不一致且相差多个数量级，则插值结果可能存在数值误差。考虑在插值之前重新缩放数据。

为样条方法选择求解器

样条方法，“slinear”、“cubic”和“quintic”在实例化时涉及求解大型稀疏线性系统。根据数据，默认求解器可能不适用。当它不适用时，您可能需要尝试可选的 solver 参数，您可以在其中选择直接求解器（scipy.sparse.linalg.spsolve）或 scipy.sparse.linalg 中的迭代求解器。您可能需要通过可选的 solver_args 参数提供其他参数（例如，您可以提供起始值或目标容差）。有关可用选项的完整列表，请参阅 scipy.sparse.linalg 文档。

或者，您可以改用旧版方法，“slinear_legacy”、“cubic_legacy”和“quintic_legacy”。这些方法允许更快地构建，但评估速度会慢得多。

使用 `nearest` 方法在半点处的舍入规则

使用 nearest 方法在半点处的舍入规则是向下舍入。

参考文献

[1]

由 Johannes Buchner 开发的 Python 包 regulargrid，参见 https://pypi.python.org/pypi/regulargrid/

[2]

维基百科，“三线性插值”，https://en.wikipedia.org/wiki/Trilinear_interpolation

[3]

Weiser, Alan, 和 Sergio E. Zarantonello。“关于分段线性多维表格插值的注释。”MATH. COMPUT. 50.181 (1988): 189-196。https://www.ams.org/journals/mcom/1988-50-181/S0025-5718-1988-0917826-0/S0025-5718-1988-0917826-0.pdf DOI:10.1090/S0025-5718-1988-0917826-0

示例

在 3-D 网格点上评估函数

作为第一个示例，我们在 3-D 网格点上评估一个简单的示例函数

>>> from scipy.interpolate import RegularGridInterpolator
>>> import numpy as np
>>> def f(x, y, z):
...     return 2 * x**3 + 3 * y**2 - z
>>> x = np.linspace(1, 4, 11)
>>> y = np.linspace(4, 7, 22)
>>> z = np.linspace(7, 9, 33)
>>> xg, yg ,zg = np.meshgrid(x, y, z, indexing='ij', sparse=True)
>>> data = f(xg, yg, zg)

data 现在是一个 3-D 数组，其中 data[i, j, k] = f(x[i], y[j], z[k])。接下来，从此数据定义一个插值函数

>>> interp = RegularGridInterpolator((x, y, z), data)

在两个点 (x,y,z) = (2.1, 6.2, 8.3) 和 (3.3, 5.2, 7.1) 处评估插值函数

>>> pts = np.array([[2.1, 6.2, 8.3],
...                 [3.3, 5.2, 7.1]])
>>> interp(pts)
array([ 125.80469388,  146.30069388])

这确实是以下值的近似

>>> f(2.1, 6.2, 8.3), f(3.3, 5.2, 7.1)
(125.54200000000002, 145.894)

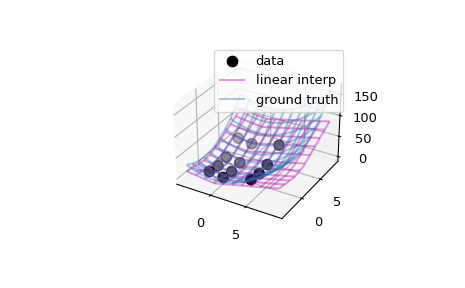
插值并外推 2D 数据集

作为第二个示例，我们插值并外推一个 2D 数据集

>>> x, y = np.array([-2, 0, 4]), np.array([-2, 0, 2, 5])
>>> def ff(x, y):
...     return x**2 + y**2

>>> xg, yg = np.meshgrid(x, y, indexing='ij')
>>> data = ff(xg, yg)
>>> interp = RegularGridInterpolator((x, y), data,
...                                  bounds_error=False, fill_value=None)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> ax.scatter(xg.ravel(), yg.ravel(), data.ravel(),
...            s=60, c='k', label='data')

在更细的网格上评估并绘制插值器

>>> xx = np.linspace(-4, 9, 31)
>>> yy = np.linspace(-4, 9, 31)
>>> X, Y = np.meshgrid(xx, yy, indexing='ij')

>>> # interpolator
>>> ax.plot_wireframe(X, Y, interp((X, Y)), rstride=3, cstride=3,
...                   alpha=0.4, color='m', label='linear interp')

>>> # ground truth
>>> ax.plot_wireframe(X, Y, ff(X, Y), rstride=3, cstride=3,
...                   alpha=0.4, label='ground truth')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-interpolate-RegularGridInterpolator-1_00_00.png

其他示例可在教程中找到。