splrep#
- scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, task=0, s=None, t=None, full_output=0, per=0, quiet=1)[source]#
查找一维曲线的B样条表示。
旧版
此函数被认为是旧版,将不再接收更新。虽然我们目前没有计划将其移除,但我们建议新代码使用更现代的替代方案。具体来说,我们建议在新代码中使用
make_splrep。给定数据集
(x[i], y[i]),确定在区间xb <= x <= xe上的 k 次平滑样条近似。- 参数:
- x, y类数组
定义曲线
y = f(x)的数据点。- w类数组,可选
严格正的一维权重数组,长度与 x 和 y 相同。这些权重用于计算加权最小二乘样条拟合。如果 y 值的误差由向量
d给出的标准差表示,则 w 应该为1/d。默认值为ones(len(x))。- xb, xe浮点数,可选
拟合区间。如果为 None,则默认分别为
x[0]和x[-1]。- k整数,可选
样条拟合的次数。建议使用三次样条。应避免使用偶数 k 值,尤其是在 s 值较小的情况下。
1 <= k <= 5。- task{1, 0, -1},可选
如果
task==0,则为给定平滑因子 s 查找t和c。如果
task==1,则为平滑因子 s 的另一个值查找t和c。必须对同一数据集(t将在内部存储和使用)进行过先前调用,且task=0或task=1。如果
task=-1,则为给定节集t查找加权最小二乘样条。这些应该是内部节,因为末端的节将自动添加。- s浮点数,可选
一个平滑条件。平滑度由满足以下条件来确定:
sum((w * (y - g))**2,axis=0) <= s,其中g(x)是(x,y)的平滑插值。用户可以使用 s 来控制拟合的紧密程度和平滑度之间的权衡。较大的 s 意味着更多的平滑,而较小的 s 值表示较少的平滑。推荐的 s 值取决于权重 w。如果权重代表 y 的标准差的倒数,那么一个好的 s 值应该在(m-sqrt(2*m),m+sqrt(2*m))范围内找到,其中m是 x、y 和 w 中的数据点数量。默认值:如果提供了权重,则s=m-sqrt(2*m)。如果没有提供权重,则s = 0.0(插值)。- t类数组,可选
task=-1所需的节。如果给定,则 task 自动设置为-1。- full_output布尔值,可选
如果非零,则返回可选输出。
- per布尔值,可选
如果非零,则数据点被认为是周期性的,周期为
x[m-1]-x[0],并返回平滑的周期样条近似。不使用y[m-1]和w[m-1]的值。默认值为零,对应于边界条件“非结”。- quiet布尔值,可选
非零以抑制消息。
- 返回:
- tck元组
一个包含节向量、B样条系数和样条次数的元组
(t,c,k)。- fp数组,可选
样条近似的残差平方加权和。
- ier整数,可选
一个关于 splrep 成功与否的整数标志。如果
ier<=0则表示成功。如果ier in [1,2,3],则发生错误但未抛出。否则会抛出错误。- msg字符串,可选
与整数标志 ier 对应的消息。
另请参阅
注意
有关样条及其导数的评估,请参阅
splev。使用 FITPACK 中的 FORTRAN 例程curfit。用户有责任确保 x 的值是唯一的。否则,
splrep将不会返回合理的结果。如果提供,节 t 必须满足 Schoenberg-Whitney 条件,即必须存在数据点
x[j]的一个子集,使得对于j=0, 1,...,n-k-2,有t[j] < x[j] < t[j+k+1]。此例程对系数数组
c进行零填充,使其与节数组t长度相同(尾部的k + 1个系数被评估例程splev和BSpline忽略)。这与splprep不同,后者不对系数进行零填充。默认边界条件是“非结”,即曲线末端的第一段和第二段是相同的多项式。更多边界条件可在
CubicSpline中找到。参考文献
[1]P. Dierckx, “An algorithm for smoothing, differentiation and integration of experimental data using spline functions”, J.Comp.Appl.Maths 1 (1975) 165-184.
[2]P. Dierckx, “A fast algorithm for smoothing data on a rectangular grid while using spline functions”, SIAM J.Numer.Anal. 19 (1982) 1286-1304.
[3]P. Dierckx, “An improved algorithm for curve fitting with spline functions”, report tw54, Dept. Computer Science,K.U. Leuven, 1981.
[4]P. Dierckx, “Curve and surface fitting with splines”, Monographs on Numerical Analysis, Oxford University Press, 1993.
示例
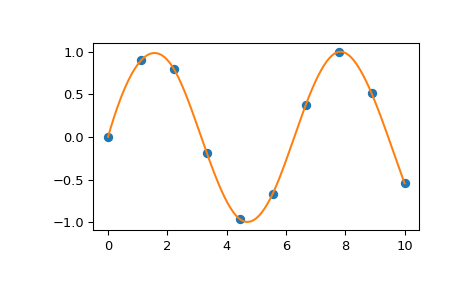
您可以使用 B 样条曲线插值一维点。更多示例可在教程中找到。
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import splev, splrep >>> x = np.linspace(0, 10, 10) >>> y = np.sin(x) >>> spl = splrep(x, y) >>> x2 = np.linspace(0, 10, 200) >>> y2 = splev(x2, spl) >>> plt.plot(x, y, 'o', x2, y2) >>> plt.show()