scipy.interpolate.

griddata#

scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)[source]#

在多维中对非结构化数据进行插值的便捷函数。

参数：

points形状为 (n, D) 的二维浮点 ndarray，或形状为 (n,) 的长度为 D 的一维 ndarray 元组。

数据点坐标。

values浮点或复数 ndarray，形状 (n,)

数据值。

xi形状为 (m, D) 的二维浮点 ndarray，或长度为 D 的 ndarray 元组，可广播到相同形状。

要插值数据点的位置。

method{'linear', 'nearest', 'cubic'}，可选

插值方法。以下之一：

nearest: 返回最接近插值点的数据点的值。更多详情请参见 NearestNDInterpolator。
linear: 将输入点集剖分成 N 维单形，并在每个单形上进行线性插值。更多详情请参见 LinearNDInterpolator。
cubic (1-D): 返回由三次样条确定的值。
cubic (2-D): 返回由分段三次、连续可微 (C1) 且近似最小曲率的多项式曲面确定的值。更多详情请参见 CloughTocher2DInterpolator。

fill_value浮点型，可选

用于填充输入点凸包外部所需点的值。如果未提供，则默认值为 nan。此选项对 'nearest' 方法无效。

rescale布尔型，可选

在执行插值之前将点重新缩放为单位立方体。如果某些输入维度具有不可公度的单位且相差多个数量级，则此功能很有用。

0.14.0 版本新增。

返回：

ndarray: 插值后的值数组。

另请参见

LinearNDInterpolator: N 维分段线性插值器。
NearestNDInterpolator: N 维最近邻插值器。
CloughTocher2DInterpolator: 二维分段三次、C1 平滑、曲率最小插值器。
interpn: 在规则网格或直角网格上的插值。
RegularGridInterpolator: 任意维度的规则网格或直角网格上的插值器（interpn 封装了此类别）。

注释

0.9 版本新增。

注意

对于规则网格上的数据，请改用 interpn。

示例

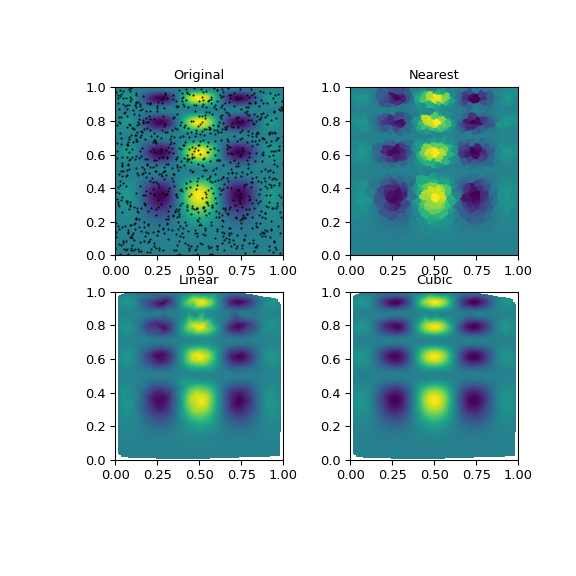
假设我们想在 [0, 1]x[0, 1] 的网格上插值二维函数

>>> import numpy as np
>>> def func(x, y):
...     return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

但我们只知道它在 1000 个数据点上的值

>>> grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]

这可以使用 griddata 完成——下面我们尝试所有插值方法

>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])

可以看出，所有方法都在某种程度上再现了精确结果，但对于这个平滑函数，分段三次插值器给出了最佳结果。

>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

（原文：One can see that the exact result is reproduced by all of the methods to some degree, but for this smooth function the piecewise cubic interpolant gives the best results）

>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
>>> plt.plot(points[:,0], points[:,1], 'k.', ms=1)
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()

../../_images/scipy-interpolate-griddata-1.png