scipy.interpolate.

barycentric_interpolate

scipy.interpolate.barycentric_interpolate(xi, yi, x, axis=0, *, der=0, rng=None)

重心插值的便利函数。

构建一个通过给定点集的多项式，然后评估该多项式。出于数值稳定性考虑，此函数不计算多项式的系数。

此函数使用“重心插值”方法，将问题视为有理函数插值的一种特殊情况。该算法在数值上相当稳定，但即便在精确计算的世界中，除非 x 坐标选择得非常仔细（切比雪夫零点（例如 cos(i*pi/n)）是一个不错的选择），否则多项式插值本身就是一个病态过程，原因在于龙格现象。

参数:

xi类数组

多项式应通过的点的 x 坐标的一维数组

yi类数组

多项式应通过的点的 y 坐标。

x标量或类数组

要评估插值函数的点。

axisint，可选

yi 数组中对应于 x 坐标值的轴。

derint 或列表或 None，可选

要评估多少个导数，或 None 表示所有可能非零的导数（即等于点数的导数），或要评估的导数列表。此数量包含函数值作为“0阶”导数。

rngnumpy.random.Generator，可选

伪随机数生成器状态。当 rng 为 None 时，将使用操作系统中的熵创建一个新的 numpy.random.Generator。其他类型（非 numpy.random.Generator）将传递给 numpy.random.default_rng 以实例化一个 Generator。

返回值:

y标量或类数组

插值结果。形状由原始数组中的插值轴替换为 x 的形状而确定。

另请参阅

BarycentricInterpolator

重心插值器

注意

插值权重的构建是一个相对较慢的过程。如果希望使用相同的 xi（但 yi 或 x 可能不同）多次调用此函数，则应使用类 BarycentricInterpolator。此函数内部使用该类。

示例

在浏览器中尝试！

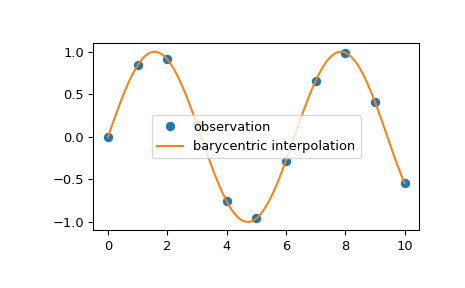
我们可以使用重心插值对二维观测数据进行插值

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import barycentric_interpolate
>>> x_observed = np.linspace(0.0, 10.0, 11)
>>> y_observed = np.sin(x_observed)
>>> x = np.linspace(min(x_observed), max(x_observed), num=100)
>>> y = barycentric_interpolate(x_observed, y_observed, x)
>>> plt.plot(x_observed, y_observed, "o", label="observation")
>>> plt.plot(x, y, label="barycentric interpolation")
>>> plt.legend()
>>> plt.show()

返回在新标签页中打开