scipy.interpolate.

krogh_interpolate

scipy.interpolate.krogh_interpolate(xi, yi, x, der=0, axis=0)

Krogh 插值的便捷函数。

更多详细信息请参见 KroghInterpolator。

参数:

xi类数组

插值点（已知 x 坐标）。

yi类数组

已知 y 坐标，形状为 (xi.size, R)。解释为长度为 R 的向量，如果 R=1 则为标量。

x类数组

要评估导数的点或多个点。

derint、list 或 None，可选

要评估的导数数量，或者为 None 表示所有可能非零的导数（即等于点数），或者是一个要评估的导数列表。此数量包括函数值作为“0阶”导数。

axisint，可选

yi 数组中对应 x 坐标值的轴。

返回:

dndarray

如果插值器的值为 R 维，则返回的数组将是导数数量乘以 N 乘以 R。如果 x 是标量，则中间维度将被删除；如果 yi 是标量，则最后一个维度将被删除。

另请参阅

KroghInterpolator

Krogh 插值器

注意

插值多项式的构建是一个相对昂贵的过程。如果需要重复评估，请考虑使用 KroghInterpolator 类（此函数就是使用该类）。

示例

在浏览器中尝试！

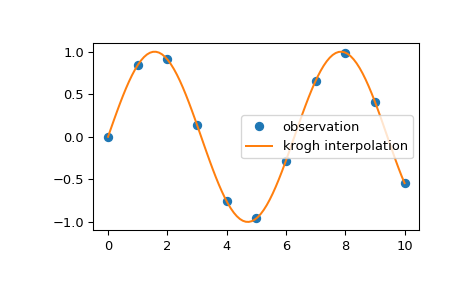
我们可以使用 Krogh 插值来插值 2D 观测数据

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import krogh_interpolate
>>> x_observed = np.linspace(0.0, 10.0, 11)
>>> y_observed = np.sin(x_observed)
>>> x = np.linspace(min(x_observed), max(x_observed), num=100)
>>> y = krogh_interpolate(x_observed, y_observed, x)
>>> plt.plot(x_observed, y_observed, "o", label="observation")
>>> plt.plot(x, y, label="krogh interpolation")
>>> plt.legend()
>>> plt.show()

返回在新标签页中打开