scipy.interpolate.

generate_knots

scipy.interpolate.generate_knots(x, y, *, w=None, xb=None, xe=None, k=3, s=0, nest=None)

生成结点向量，直到满足最小二乘 (LSQ) 准则。

参数:

x, yarray_like

定义曲线 y = f(x) 的数据点。

warray_like, 可选

权重。

xbfloat, 可选

近似区间的边界。如果为 None（默认），则设置为 x[0]。

xefloat, 可选

近似区间的边界。如果为 None（默认），则设置为 x[-1]。

kint, 可选

样条的次数。默认为三次样条，k = 3。

sfloat, 可选

平滑因子。默认为 s = 0。

nestint, 可选

当至少放置了这么多结点时停止。

生成:

tndarray

结点向量，结点数量递增。此生成器是有限的：当平滑准则满足时，或者当结点数量超过最大值（用户提供的 nest 或 x.size + k + 1，即插值样条的结点向量）时，它会停止。

备注

该例程生成长度递增的连续结点向量，从 2*(k+1) 到 len(x) + k + 1，旨在使最小二乘样条与数据偏差较大的区域结点更密集。

当达到最大结点数 len(x) + k + 1 时（这发生在 s 较小且 nest 较大时），生成器停止，最终输出的是采用非结点边界条件的插值结点。

结点位于数据点处，除非 k 为偶数且结点数为 len(x) + k + 1。在这种情况下，生成器的最终输出在 Greville 点处具有内部结点，即 (x[1:] + x[:-1]) / 2。

在版本 1.15.0 中添加。

示例

在浏览器中尝试！

生成一些带噪声的数据并拟合一系列最小二乘样条

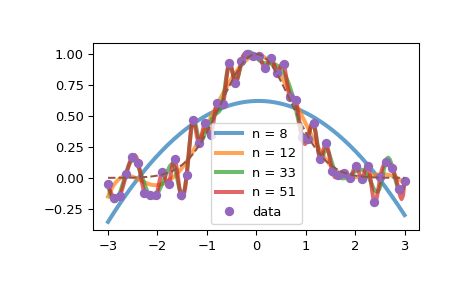
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import make_lsq_spline, generate_knots
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(size=50)

>>> knots = list(generate_knots(x, y, s=1e-10))
>>> for t in knots[::3]:
...     spl = make_lsq_spline(x, y, t)
...     xs = xs = np.linspace(-3, 3, 201)
...     plt.plot(xs, spl(xs), '-', label=f'n = {len(t)}', lw=3, alpha=0.7)
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xs, np.exp(-xs**2), '--')
>>> plt.legend()

请注意，增加结点数量会使结果越来越紧密地跟随数据。

另请注意，生成器的一个步骤可能会添加多个结点

>>> [len(t) for t in knots]
[8, 9, 10, 12, 16, 24, 40, 48, 52, 54]

返回在新标签页中打开