scipy.interpolate.

AAA#

class scipy.interpolate.AAA(x, y, *, rtol=None, max_terms=100, clean_up=True, clean_up_tol=1e-13)[源]#

AAA 实数或复数有理逼近。

如 [1] 中所述，AAA 算法是一种贪婪算法，用于在实数或复数点集上进行有理函数逼近。有理逼近以重心形式表示，从中可以计算出根（零点）、极点和残差。

参数:
x1D 数组状，形状 (n,)

包含自变量值的一维数组。值可以是实数或复数，但必须是有限的。

y1D 数组状，形状 (n,)

函数值 f(x)。 values 中无限和 NaN 的值以及 points 中相应的值将被丢弃。

rtol浮点数，可选

相对容差，默认为 eps**0.75。如果 values 中一小部分条目远大于其余条目，则默认容差可能过于宽松。如果容差过紧，则逼近可能包含 Froissart 对偶点，或算法可能完全无法收敛。

max_terms整数，可选

重心表示中的最大项数，默认为 100。必须大于或等于一。

clean_up布尔值，可选

自动移除 Froissart 对偶点，默认为 True。有关详细信息，请参阅注释。

clean_up_tol浮点数，可选

清理程序认为，残差小于此数值乘以 values 的几何平均值再乘以到 points 的最小距离的极点是虚假的，默认为 1e-13。有关详细信息，请参阅注释。

属性:
support_points数组

逼近的支持点。这些是所提供 x 的一个子集，逼近在此处严格插值 y。有关详细信息，请参阅注释。

support_values数组

逼近在 support_points 处的值。

weights数组

重心逼近的权重。

errors数组

AAA 连续迭代中 points 上的误差 \(|f(z) - r(z)|_\infty\)。

方法

__call__(z)

在给定值处评估有理逼近。

clean_up([cleanup_tol])

自动移除 Froissart 对偶点。

极点()

计算有理逼近的极点。

残差()

计算逼近极点的残差。

根()

计算有理逼近的零点。
警告:
运行时警告

如果在 max_terms 次迭代中未达到 rtol。

另请参阅

FloaterHormannInterpolator

Floater-Hormann 重心有理插值。

pade

Padé 逼近。

注释

在第 \(m\) 次迭代时（此时逼近的分子和分母中都有 \(m\) 项），AAA 算法中的有理逼近采用重心形式

\[r(z) = n(z)/d(z) = \frac{\sum_{j=1}^m\ w_j f_j / (z - z_j)}{\sum_{j=1}^m w_j / (z - z_j)},\]

其中 \(z_1,\dots,z_m\) 是从 x 中选择的实数或复数支持点，\(f_1,\dots,f_m\) 是从 y 中对应的实数或复数数据值，而 \(w_1,\dots,w_m\) 是实数或复数权重。

算法的每次迭代都包含两个部分：贪婪选择下一个支持点和计算权重。每次迭代的第一部分是从剩余未选定的 x 中选择要添加的下一个支持点 \(z_{m+1}\)，以使非线性残差 \(|f(z_{m+1}) - n(z_{m+1})/d(z_{m+1})|\) 最大化。当此最大值小于 rtol * np.linalg.norm(f, ord=np.inf) 时，算法终止。这意味着插值属性仅在一定容差范围内满足，但在支持点处，逼近精确插值所提供的数据。

在每次迭代的第二部分中，选择权重 \(w_j\) 以解决最小二乘问题

\[\text{minimise}_{w_j}|fd - n| \quad \text{subject to} \quad \sum_{j=1}^{m+1} w_j = 1,\]

在 x 的未选定元素上。

处理有理逼近的一个挑战是 Froissart 对偶点的存在，它们要么是残差极小的极点，要么是足够接近以几乎抵消的极点-零点对，参见 [2]。AAA 算法的贪婪性质意味着 Froissart 对偶点很少见。然而，如果 rtol 设置得过紧，则逼近将停滞，并出现许多 Froissart 对偶点。Froissart 对偶点通常可以通过移除支持点，然后重新解决最小二乘问题来移除。如果满足以下条件，则移除支持点 \(z_j\)（它是残差为 \(\alpha\) 的极点 \(a\) 最近的支持点）

\[|\alpha| / |z_j - a| < \verb|clean_up_tol| \cdot \tilde{f},\]

其中 \(\tilde{f}\) 是 support_values 的几何平均值。

参考文献

[1] (1,2,3)

Y. Nakatsukasa, O. Sete, and L. N. Trefethen, “The AAA algorithm for rational approximation”, SIAM J. Sci. Comp. 40 (2018), A1494-A1522. DOI:10.1137/16M1106122

[2]

J. Gilewicz and M. Pindor, Pade approximants and noise: rational functions, J. Comp. Appl. Math. 105 (1999), pp. 285-297. DOI:10.1016/S0377-0427(02)00674-X

示例

这里我们重现了 [1] 中的一些数值示例，以展示此方法提供的功能。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import AAA
>>> import warnings

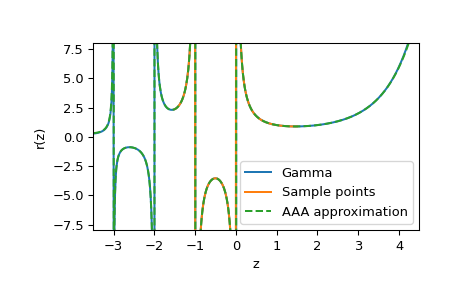
对于第一个示例，我们通过从 [-1.5, 1.5] 中的 100 个样本外推，来逼近 [-3.5, 4.5] 上的伽马函数。

>>> from scipy.special import gamma
>>> sample_points = np.linspace(-1.5, 1.5, num=100)
>>> r = AAA(sample_points, gamma(sample_points))
>>> z = np.linspace(-3.5, 4.5, num=1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(z, gamma(z), label="Gamma")
>>> ax.plot(sample_points, gamma(sample_points), label="Sample points")
>>> ax.plot(z, r(z).real, '--', label="AAA approximation")
>>> ax.set(xlabel="z", ylabel="r(z)", ylim=[-8, 8], xlim=[-3.5, 4.5])
>>> ax.legend()
>>> plt.show()
../../_images/scipy-interpolate-AAA-1_00_00.png

我们还可以查看有理逼近的极点及其残差

>>> order = np.argsort(r.poles())
>>> r.poles()[order]
array([-3.81591039e+00+0.j        , -3.00269049e+00+0.j        ,
       -1.99999988e+00+0.j        , -1.00000000e+00+0.j        ,
        5.85842812e-17+0.j        ,  4.77485458e+00-3.06919376j,
        4.77485458e+00+3.06919376j,  5.29095868e+00-0.97373072j,
        5.29095868e+00+0.97373072j])
>>> r.residues()[order]
array([ 0.03658074 +0.j        , -0.16915426 -0.j        ,
        0.49999915 +0.j        , -1.         +0.j        ,
        1.         +0.j        , -0.81132013 -2.30193429j,
       -0.81132013 +2.30193429j,  0.87326839+10.70148546j,
        0.87326839-10.70148546j])

对于第二个示例，我们调用 AAA，使用 1000 个在复平面上绕原点螺旋 7.5 圈的点。

>>> z = np.exp(np.linspace(-0.5, 0.5 + 15j*np.pi, 1000))
>>> r = AAA(z, np.tan(np.pi*z/2), rtol=1e-13)

我们看到 AAA 经过 12 步收敛，误差如下

>>> r.errors.size
12
>>> r.errors
array([2.49261500e+01, 4.28045609e+01, 1.71346935e+01, 8.65055336e-02,
       1.27106444e-02, 9.90889874e-04, 5.86910543e-05, 1.28735561e-06,
       3.57007424e-08, 6.37007837e-10, 1.67103357e-11, 1.17112299e-13])

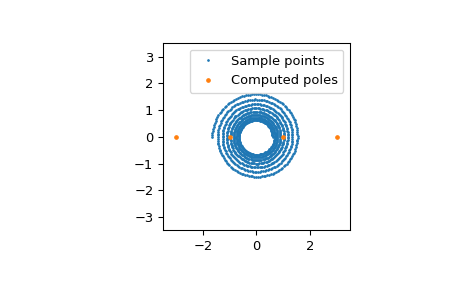
我们还可以绘制计算出的极点

>>> fig, ax = plt.subplots()
>>> ax.plot(z.real, z.imag, '.', markersize=2, label="Sample points")
>>> ax.plot(r.poles().real, r.poles().imag, '.', markersize=5,
...         label="Computed poles")
>>> ax.set(xlim=[-3.5, 3.5], ylim=[-3.5, 3.5], aspect="equal")
>>> ax.legend()
>>> plt.show()
../../_images/scipy-interpolate-AAA-1_01_00.png

现在，我们使用 [1] 中的一个示例，演示如何使用 clean_up 方法移除 Froissart 对偶点。这里我们通过在 1000 个单位根处采样，来逼近函数 \(f(z)=\log(2 + z^4)/(1 + 16z^4)\)。算法在 rtol=0 和 clean_up=False 的设置下运行，以故意导致 Froissart 对偶点的出现。

>>> z = np.exp(1j*2*np.pi*np.linspace(0,1, num=1000))
>>> def f(z):
...     return np.log(2 + z**4)/(1 - 16*z**4)
>>> with warnings.catch_warnings():  # filter convergence warning due to rtol=0
...     warnings.simplefilter('ignore', RuntimeWarning)
...     r = AAA(z, f(z), rtol=0, max_terms=50, clean_up=False)
>>> mask = np.abs(r.residues()) < 1e-13
>>> fig, axs = plt.subplots(ncols=2)
>>> axs[0].plot(r.poles().real[~mask], r.poles().imag[~mask], '.')
>>> axs[0].plot(r.poles().real[mask], r.poles().imag[mask], 'r.')

现在我们调用 clean_up 方法来移除 Froissart 对偶点。

>>> with warnings.catch_warnings():
...     warnings.simplefilter('ignore', RuntimeWarning)
...     r.clean_up()
4  # may vary
>>> mask = np.abs(r.residues()) < 1e-13
>>> axs[1].plot(r.poles().real[~mask], r.poles().imag[~mask], '.')
>>> axs[1].plot(r.poles().real[mask], r.poles().imag[mask], 'r.')
>>> plt.show()
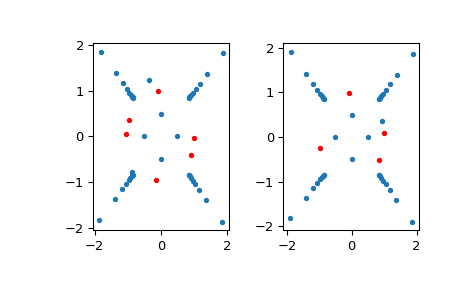
../../_images/scipy-interpolate-AAA-1_02_00.png

左图显示了在 clean_up=False 逼近之前的极点，其中绝对值小于 10^-13 的残差极点以红色显示。右图显示了调用 clean_up 方法后的极点。

本页内容