scipy.interpolate.

FloaterHormannInterpolator

class scipy.interpolate.FloaterHormannInterpolator(points, values, *, d=3)

Floater-Hormann 重心有理插值器（在实轴上C∞光滑）。

如[1]中所述，Floater 和 Hormann 方法计算无实轴极点的重心有理插值器的权重。

参数:

x1D array_like, 形状 (n,)

包含自变量值的一维类数组。值可以是实数或复数，但必须是有限的。

yarray_like, 形状 (n, …)

包含因变量值的数组。y 的无限值和 NaN 值以及 x 的对应值将被丢弃。

d整型, 默认值: 3

满足 0 <= d < n 的整数。Floater-Hormann 插值将 n - d 个 d 次多项式混合在一起；当 d = n - 1 时，这等同于多项式插值。

属性:

weights数组

重心逼近的权重。

方法

__call__(z)	计算给定值处的有理逼近。
poles()	计算有理逼近的极点。
residues()	计算逼近的极点留数。
roots()	计算有理逼近的零点。

另请参阅

AAA

实函数和复函数的重心有理逼近。

pade

Padé 逼近。

说明

Floater-Hormann 插值器是一个有理函数，以 \(O(h^{d+1})\) 的逼近阶插值数据。该有理函数将 n - d 个 d 次多项式混合在一起，生成一个在实轴上没有极点的有理插值器，这与 AAA 不同。插值器由下式给出

\[r(x) = \frac{\sum_{i=0}^{n-d} \lambda_i(x) p_i(x)} {\sum_{i=0}^{n-d} \lambda_i(x)},\]

其中 \(p_i(x)\) 是通过点 \((x_i,y_i),\dots,(x_{i+d},y_{i+d})\) 的最多 d 次插值多项式，\(\lambda_i(z)\) 是由下式定义的混合函数：

\[\lambda_i(x) = \frac{(-1)^i}{(x - x_i)\cdots(x - x_{i+d})}.\]

当 d = n - 1 时，这简化为多项式插值。

由于其稳定性，以下方程的重心表示用于计算：

\[r(z) = \frac{\sum_{k=1}^m\ w_k f_k / (x - x_k)}{\sum_{k=1}^m w_k / (x - x_k)},\]

其中权重 \(w_j\) 计算如下：

\[\begin{split}w_k &= (-1)^{k - d} \sum_{i \in J_k} \prod_{j = i, j \neq k}^{i + d} 1/|x_k - x_j|, \\ J_k &= \{ i \in I: k - d \leq i \leq k\},\\ I &= \{0, 1, \dots, n - d\}.\end{split}\]

参考文献

[1]

M.S. Floater and K. Hormann, “Barycentric rational interpolation with no poles and high rates of approximation”, Numer. Math. 107, 315 (2007). DOI:10.1007/s00211-007-0093-y

示例

在浏览器中尝试！

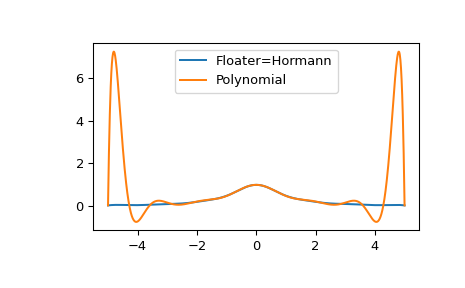
在这里，我们将该方法与多项式插值进行比较，在一个多项式插值由于龙格现象而失败的例子中。

>>> import numpy as np
>>> from scipy.interpolate import (FloaterHormannInterpolator,
...                                BarycentricInterpolator)
>>> def f(x):
...     return 1/(1 + x**2)
>>> x = np.linspace(-5, 5, num=15)
>>> r = FloaterHormannInterpolator(x, f(x))
>>> p = BarycentricInterpolator(x, f(x))
>>> xx = np.linspace(-5, 5, num=1000)
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.plot(xx, f(xx), label="f(x)")
>>> ax.plot(xx, r(xx), "--", label="Floater-Hormann")
>>> ax.plot(xx, p(xx), "--", label="Polynomial")
>>> ax.legend()
>>> plt.show()

返回在新标签页中打开