scipy.spatial.transform.

Rotation#

class scipy.spatial.transform.Rotation(quat, normalize=True, copy=True, scalar_first=False)[source]#

3 维旋转。

此类提供了一个接口，用于初始化和表示以下形式的旋转：

四元数
旋转矩阵
旋转向量
修正罗德里格参数
欧拉角
达文波特角（广义欧拉角）

支持以下旋转操作：

对向量的应用
旋转合成
旋转求逆
旋转索引

一个 Rotation 实例可以包含单个旋转变换或具有多个前导维度的旋转。例如，可以有一个 (N, M, K) 旋转的 N 维数组。当应用于其他旋转或向量时，将应用标准广播规则。

支持在旋转内进行索引，以访问存储在 Rotation 实例中的旋转子集。

要创建 Rotation 对象，请使用 from_... 方法（参见下面的示例）。Rotation(...) 不应直接实例化。

属性:

单个: 此实例是否代表单个旋转。

方法

`__len__`()	此对象中包含的旋转数量。
`from_quat`(quat, *[, scalar_first])	从四元数初始化。
`from_matrix`(matrix, *[, assume_valid])	从旋转矩阵初始化。
`from_rotvec`(rotvec[, degrees])	从旋转向量初始化。
`from_mrp`(mrp)	从修正罗德里格参数 (MRPs) 初始化。
`from_euler`(seq, angles[, degrees])	从欧拉角初始化。
`from_davenport`(axes, order, angles[, degrees])	从达文波特角初始化。
`as_quat`([canonical, scalar_first])	表示为四元数。
`as_matrix`()	表示为旋转矩阵。
`as_rotvec`([degrees])	表示为旋转向量。
`as_mrp`()	表示为修正罗德里格参数 (MRPs)。
`as_euler`(seq[, degrees, suppress_warnings])	表示为欧拉角。
`as_davenport`(axes, order[, degrees, ...])	表示为达文波特角。
`concatenate`(rotations)	将一系列 `Rotation` 对象连接成一个对象。
`apply`(vectors[, inverse])	将此旋转应用于一组向量。
`__mul__`(other)	将此旋转与其他旋转合成。
`__pow__`(n[, modulus])	将此旋转与自身合成 n 次。
`inv`()	反转此旋转。
`magnitude`()	获取旋转的幅度。
`approx_equal`(other[, atol, degrees])	确定另一个旋转是否与此旋转大致相等。
`mean`([weights, axis])	获取旋转的平均值。
`reduce`([left, right, return_indices])	使用提供的旋转组减少此旋转。
`create_group`(group[, axis])	创建 3D 旋转组。
`__getitem__`(indexer)	从对象中提取给定索引处的旋转。
`identity`([num, shape])	获取恒等旋转。
`random`([num, rng, shape, random_state])	生成在球体上均匀分布的旋转。
`align_vectors`(a, b[, weights, ...])	估计一个旋转，以最佳地对齐两组向量。

另请参阅

球面线性插值

附注

在 1.2.0 版本中添加。

示例

>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

一个 Rotation 实例可以以上述任何一种格式初始化，并转换为任何其他格式。底层对象与用于初始化的表示形式无关。

考虑绕 z 轴逆时针旋转 90 度。这对应于以下四元数（标量在后的格式）

>>> r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])

旋转可以用任何其他格式表示

>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
[ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
[ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

相同的旋转可以使用旋转矩阵初始化

>>> r = R.from_matrix([[0, -1, 0],
...                    [1, 0, 0],
...                    [0, 0, 1]])

以其他格式表示

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

对应于此旋转的旋转向量由下式给出

>>> r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))

以其他格式表示

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

from_euler 方法在它支持的输入格式范围方面非常灵活。这里我们初始化围绕单个轴的单个旋转

>>> r = R.from_euler('z', 90, degrees=True)

同样，该对象与表示形式无关，可以转换为任何其他格式

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])

也可以使用任何 from_... 函数在一个实例中初始化多个旋转。这里我们使用 from_euler 方法初始化 3 个旋转的堆栈

>>> r = R.from_euler('zyx', [
... [90, 0, 0],
... [0, 45, 0],
... [45, 60, 30]], degrees=True)

现在其他表示形式也返回 3 个旋转的堆栈。例如

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

将上述旋转应用于向量

>>> v = [1, 2, 3]
>>> r.apply(v)
array([[-2.        ,  1.        ,  3.        ],
       [ 2.82842712,  2.        ,  1.41421356],
       [ 2.24452282,  0.78093109,  2.89002836]])

一个 Rotation 实例可以像 ND 数组一样进行索引和切片

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])
>>> p = r[0]
>>> p.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> q = r[1:3]
>>> q.as_quat()
array([[0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

事实上，它可以转换为 numpy.array

>>> r_array = np.asarray(r)
>>> r_array.shape
(3,)
>>> r_array[0].as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])

可以使用 * 运算符组合多个旋转

>>> r1 = R.from_euler('z', 90, degrees=True)
>>> r2 = R.from_rotvec([np.pi/4, 0, 0])
>>> v = [1, 2, 3]
>>> r2.apply(r1.apply(v))
array([-2.        , -1.41421356,  2.82842712])
>>> r3 = r2 * r1 # Note the order
>>> r3.apply(v)
array([-2.        , -1.41421356,  2.82842712])

一个旋转可以使用 ** 运算符与自身组合

>>> p = R.from_rotvec([1, 0, 0])
>>> q = p ** 2
>>> q.as_rotvec()
array([2., 0., 0.])

最后，也可以反转旋转

>>> r1 = R.from_euler('z', [[90], [45]], degrees=True)
>>> r2 = r1.inv()
>>> r2.as_euler('zyx', degrees=True)
array([[-90.,   0.,   0.],
       [-45.,   0.,   0.]])

以下函数可用于使用 Matplotlib 绘制旋转，通过显示它们如何变换标准 x、y、z 坐标轴

>>> import matplotlib.pyplot as plt

>>> def plot_rotated_axes(ax, r, name=None, offset=(0, 0, 0), scale=1):
...     colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
...     loc = np.array([offset, offset])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + loc[0]
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*offset, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

创建三个旋转 - 恒等旋转和两个使用内禀和外禀约定的欧拉旋转

>>> r0 = R.identity()
>>> r1 = R.from_euler("ZYX", [90, -30, 0], degrees=True)  # intrinsic
>>> r2 = R.from_euler("zyx", [90, -30, 0], degrees=True)  # extrinsic

将所有三个旋转添加到单个图中

>>> ax = plt.figure().add_subplot(projection="3d", proj_type="ortho")
>>> plot_rotated_axes(ax, r0, name="r0", offset=(0, 0, 0))
>>> plot_rotated_axes(ax, r1, name="r1", offset=(3, 0, 0))
>>> plot_rotated_axes(ax, r2, name="r2", offset=(6, 0, 0))
>>> _ = ax.annotate(
...     "r0: Identity Rotation\n"
...     "r1: Intrinsic Euler Rotation (ZYX)\n"
...     "r2: Extrinsic Euler Rotation (zyx)",
...     xy=(0.6, 0.7), xycoords="axes fraction", ha="left"
... )
>>> ax.set(xlim=(-1.25, 7.25), ylim=(-1.25, 1.25), zlim=(-1.25, 1.25))
>>> ax.set(xticks=range(-1, 8), yticks=[-1, 0, 1], zticks=[-1, 0, 1])
>>> ax.set_aspect("equal", adjustable="box")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.tight_layout()

显示图

>>> plt.show()

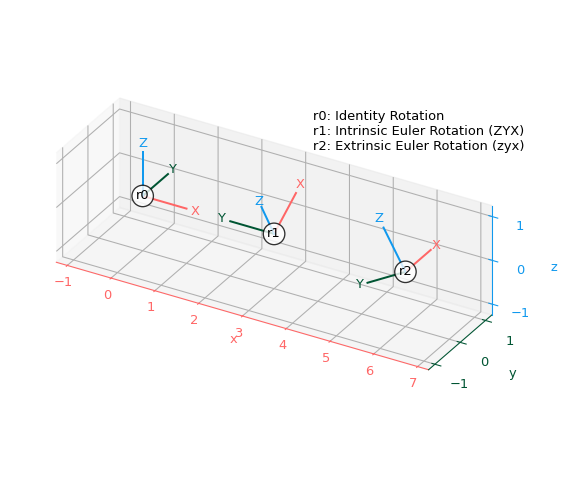
../../_images/scipy-spatial-transform-Rotation-1_00_00.png

这些示例概述了 Rotation 类并突出了主要功能。有关支持的输入和输出格式范围的更详细示例，请查阅各个方法的示例。