scipy.signal.

dstep#

scipy.signal.dstep(system, x0=None, t=None, n=None)[source]#

离散时间系统的阶跃响应。

参数:

systemdlti | tuple

LTI 类 dlti 的实例或描述系统的元组。元组中元素的数量决定了解释方式。即：

system: LTI 类 dlti 的实例。请注意，也允许派生实例，例如 TransferFunction、ZerosPolesGain 或 StateSpace 的实例。
(num, den, dt): 如 TransferFunction 中所述的有理多项式。多项式的系数应按降幂顺序指定，例如，z² + 3z + 5 将表示为 [1, 3, 5]。
(zeros, poles, gain, dt): 如 ZerosPolesGain 中所述的零点、极点、增益形式。
(A, B, C, D, dt): 如 StateSpace 中所述的状态空间形式。

x0array_like, optional

初始状态向量。默认为零。

tarray_like, optional

时间点。如果未给出则计算。

nint, optional

要计算的时间点数（如果未给出 t）。

返回:

toutndarray: 输出时间点，为一维数组。
youttuple of ndarray: 系统的阶跃响应。元组的每个元素表示系统根据对每个输入的阶跃响应产生的输出。

另请参阅

step, dimpulse, dlsim, cont2discrete

示例

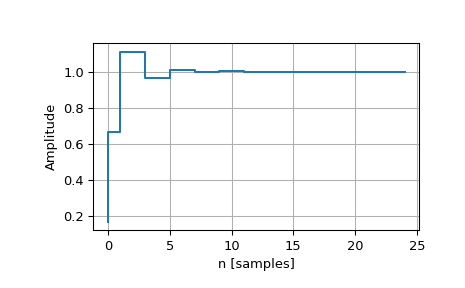
以下示例说明如何创建数字巴特沃斯滤波器并绘制其阶跃响应

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
...
>>> dt = 1  # sampling interval is one => time unit is sample number
>>> bb, aa = signal.butter(3, 0.25, fs=1/dt)
>>> t, y = signal.dstep((bb, aa, dt), n=25)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.step(t, np.squeeze(y), '.-', where='post')
>>> ax0.set_title(r"Step Response of a $3^\text{rd}$ Order Butterworth Filter")
>>> ax0.set(xlabel='Sample number', ylabel='Amplitude', ylim=(0, 1.1*np.max(y)))
>>> ax0.grid()
>>> plt.show()