scipy.signal.

dfreqresp#

scipy.signal.dfreqresp(system, w=None, n=10000, whole=False)[源]#

计算离散时间系统的频率响应。

参数:
systemdlti | tuple

dlti LTI 类的一个实例或描述该系统的元组。元组中元素的数量决定了其解释方式。即：

  • system: dlti LTI 类的实例。请注意，也允许使用派生实例，例如 TransferFunction、ZerosPolesGain 或 StateSpace 的实例。

  • (num, den, dt): TransferFunction 中描述的有理多项式。多项式的系数应按降幂顺序指定，例如，z² + 3z + 5 将表示为 [1, 3, 5]。

  • (zeros, poles, gain, dt): ZerosPolesGain 中描述的零点、极点、增益形式。

  • (A, B, C, D, dt): StateSpace 中描述的状态空间形式。

warray_like, optional

频率数组（以弧度/采样为单位）。将为该数组中的每个值计算幅度和相位数据。如果未给出，将计算一组合理的频率。

nint, optional

如果未给出 w，则要计算的频率点数。n 个频率在选定区间内以对数方式等间距排列，以包含系统零极点的影响。

wholebool, optional

通常，如果未给出“w”，则频率从 0 计算到奈奎斯特频率，即 π 弧度/采样（单位圆的上半部分）。如果 whole 为 True，则计算从 0 到 2π 弧度/采样的频率。

返回:
w1D ndarray

频率数组 [弧度/采样]

H1D ndarray

复数幅度值数组

备注

如果 system 传入 (num, den)，则分子和分母的系数都应按降幂顺序指定（例如，z^2 + 3z + 5 将表示为 [1, 3, 5]）。

0.18.0 版新增。

示例

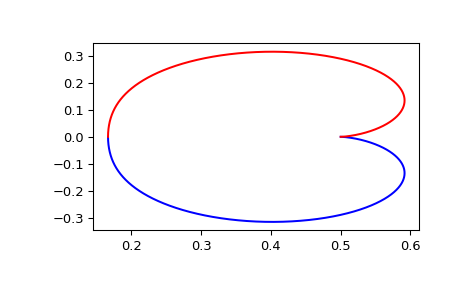
以下示例生成了传递函数 \(H(z) = \frac{1}{z^2 + 2z + 3}\) 的奈奎斯特图，采样时间为 0.05 秒。

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> sys = signal.TransferFunction([1], [1, 2, 3], dt=0.05)  # construct H(z)
>>> w, H = signal.dfreqresp(sys)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.plot(H.real, H.imag, label=r"$H(z=e^{+j\omega})$")
>>> ax0.plot(H.real, -H.imag, label=r"$H(z=e^{-j\omega})$")
>>> ax0.set_title(r"Nyquist Plot of $H(z) = 1 / (z^2 + 2z + 3)$")
>>> ax0.set(xlabel=r"$\text{Re}\{z\}$", ylabel=r"$\text{Im}\{z\}$",
...         xlim=(-0.2, 0.65), aspect='equal')
>>> ax0.plot(H[0].real, H[0].imag, 'k.')  # mark H(exp(1j*w[0]))
>>> ax0.text(0.2, 0, r"$H(e^{j0})$")
>>> ax0.grid(True)
>>> ax0.legend()
>>> plt.show()
../../_images/scipy-signal-dfreqresp-1.png
本页内容