scipy.signal.

dbode#

scipy.signal.dbode(system, w=None, n=100)[源代码]#

计算离散时间系统的伯德幅度和相位数据。

参数:

systemdlti | 元组

LTI 类 dlti 的实例，或描述系统的元组。元组中元素的数量决定了其解释方式。例如：

system: LTI 类 dlti 的实例。请注意，也允许使用派生实例，例如 TransferFunction、ZerosPolesGain 或 StateSpace 的实例。
(num, den, dt): TransferFunction 中描述的有理多项式。多项式的系数应按降幂顺序指定，例如，z² + 3z + 5 将表示为 [1, 3, 5]。
(zeros, poles, gain, dt): ZerosPolesGain 中描述的零点、极点、增益形式。
(A, B, C, D, dt): StateSpace 中描述的状态空间形式。

warray_like, 可选

频率数组，归一化到奈奎斯特频率 π，即单位为弧度/样本。将为该数组中的每个值计算幅度和相位数据。如果未给出，将计算一组合理的值。

nint, 可选

如果未给出 w，则计算的频率点数。这 n 个频率在选择的区间内对数分布，该区间旨在包含系统零点和极点的影响。

返回:

w1D ndarray: 频率数组，归一化到奈奎斯特频率 np.pi/dt，其中 dt 是 system 参数的采样间隔。假设 dt 以秒为单位，则单位为 rad/s。
mag1D ndarray: 幅度数组，单位为 dB
phase1D ndarray: 相位数组，单位为度

另请参阅

dfreqresp, dlti, TransferFunction, ZerosPolesGain, StateSpace

备注

此函数是 dfreqresp 的便捷包装器，用于从计算出的频率响应复数值振幅中提取幅度和相位。

在 0.18.0 版本中新增。

示例

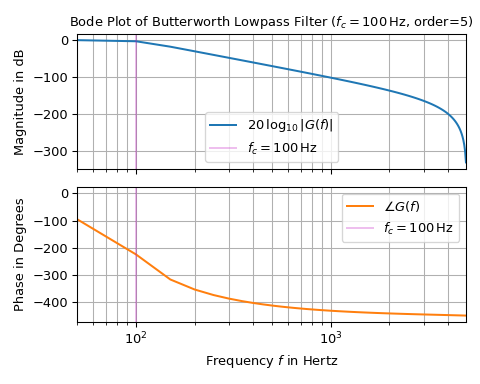
以下示例展示了如何创建具有 100 Hz 截止频率的 5 阶巴特沃斯低通滤波器的伯德图

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy import signal
...
>>> T = 1e-4  # sampling interval in s
>>> f_c, o = 1e2, 5  # corner frequency in Hz (i.e., -3 dB value) and filter order
>>> bb, aa = signal.butter(o, f_c, 'lowpass', fs=1/T)
...
>>> w, mag, phase = signal.dbode((bb, aa, T))
>>> w /= 2*np.pi  # convert unit of frequency into Hertz
...
>>> fg, (ax0, ax1) = plt.subplots(2, 1, sharex='all', figsize=(5, 4),
...                               tight_layout=True)
>>> ax0.set_title("Bode Plot of Butterworth Lowpass Filter " +
...               rf"($f_c={f_c:g}\,$Hz, order={o})")
>>> ax0.set_ylabel(r"Magnitude in dB")
>>> ax1.set(ylabel=r"Phase in Degrees",
...         xlabel="Frequency $f$ in Hertz", xlim=(w[1], w[-1]))
>>> ax0.semilogx(w, mag, 'C0-', label=r"$20\,\log_{10}|G(f)|$")  # Magnitude plot
>>> ax1.semilogx(w, phase, 'C1-', label=r"$\angle G(f)$")  # Phase plot
...
>>> for ax_ in (ax0, ax1):
...     ax_.axvline(f_c, color='m', alpha=0.25, label=rf"${f_c=:g}\,$Hz")
...     ax_.grid(which='both', axis='x')  # plot major & minor vertical grid lines
...     ax_.grid(which='major', axis='y')
...     ax_.legend()
>>> plt.show()