scipy.stats.genhyperbolic

scipy.stats.genhyperbolic = <scipy.stats._continuous_distns.genhyperbolic_gen object>

广义双曲连续随机变量。

作为 rv_continuous 类的实例，genhyperbolic 对象继承了它的一组通用方法（请参见下面的完整列表），并使用特定于此特定分布的详细信息来完成它们。

方法

rvs(p, a, b, loc=0, scale=1, size=1, random_state=None)	随机变量。
pdf(x, p, a, b, loc=0, scale=1)	概率密度函数。
logpdf(x, p, a, b, loc=0, scale=1)	概率密度函数的对数。
cdf(x, p, a, b, loc=0, scale=1)	累积分布函数。
logcdf(x, p, a, b, loc=0, scale=1)	累积分布函数的对数。
sf(x, p, a, b, loc=0, scale=1)	生存函数（也定义为 1 - cdf，但 sf 有时更准确）。
logsf(x, p, a, b, loc=0, scale=1)	生存函数的对数。
ppf(q, p, a, b, loc=0, scale=1)	百分点函数（cdf 的反函数 - 百分位数）。
isf(q, p, a, b, loc=0, scale=1)	逆生存函数（sf 的反函数）。
moment(order, p, a, b, loc=0, scale=1)	指定阶的非中心矩。
stats(p, a, b, loc=0, scale=1, moments=’mv’)	均值('m')、方差('v')、偏度('s') 和/或峰度('k')。
entropy(p, a, b, loc=0, scale=1)	RV 的（微分）熵。
fit(data)	通用数据的参数估计。 有关关键字参数的详细文档，请参阅 scipy.stats.rv_continuous.fit。
expect(func, args=(p, a, b), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	具有相对于分布的函数（一个参数）的期望值。
median(p, a, b, loc=0, scale=1)	分布的中位数。
mean(p, a, b, loc=0, scale=1)	分布的均值。
var(p, a, b, loc=0, scale=1)	分布的方差。
std(p, a, b, loc=0, scale=1)	分布的标准偏差。
interval(confidence, p, a, b, loc=0, scale=1)	中位数周围具有相等面积的置信区间。

参见

t, norminvgauss, geninvgauss, laplace, cauchy

注释

genhyperbolic 的概率密度函数为

\[f(x, p, a, b) = \frac{(a^2 - b^2)^{p/2}} {\sqrt{2\pi}a^{p-1/2} K_p\Big(\sqrt{a^2 - b^2}\Big)} e^{bx} \times \frac{K_{p - 1/2} (a \sqrt{1 + x^2})} {(\sqrt{1 + x^2})^{1/2 - p}}\]

对于 \(x, p \in ( - \infty; \infty)\), \(|b| < a\) 如果 \(p \ge 0\), \(|b| \le a\) 如果 \(p < 0\). \(K_{p}(.)\) 表示第二类和阶 \(p\) 的修正贝塞尔函数 (scipy.special.kv)

genhyperbolic 将 p 作为尾部参数，a 作为形状参数，b 作为偏度参数。

上面的概率密度以“标准化”形式定义。 要移动和/或缩放分布，请使用 loc 和 scale 参数。 具体来说，genhyperbolic.pdf(x, p, a, b, loc, scale) 与 genhyperbolic.pdf(y, p, a, b) / scale 完全等效，其中 y = (x - loc) / scale。 请注意，移动分布的位置不会使其成为“非中心”分布； 一些分布的非中心推广可以在单独的类中使用。

广义双曲分布的原始参数化可以在 [1] 中找到，如下所示

\[f(x, \lambda, \alpha, \beta, \delta, \mu) = \frac{(\gamma/\delta)^\lambda}{\sqrt{2\pi}K_\lambda(\delta \gamma)} e^{\beta (x - \mu)} \times \frac{K_{\lambda - 1/2} (\alpha \sqrt{\delta^2 + (x - \mu)^2})} {(\sqrt{\delta^2 + (x - \mu)^2} / \alpha)^{1/2 - \lambda}}\]

对于 \(x \in ( - \infty; \infty)\), \(\gamma := \sqrt{\alpha^2 - \beta^2}\), \(\lambda, \mu \in ( - \infty; \infty)\), \(\delta \ge 0, |\beta| < \alpha\) 如果 \(\lambda \ge 0\), \(\delta > 0, |\beta| \le \alpha\) 如果 \(\lambda < 0\).

在 SciPy 中实现的基于位置-尺度的参数化基于 [2]，其中 \(a = \alpha\delta\), \(b = \beta\delta\), \(p = \lambda\), \(scale=\delta\) 和 \(loc=\mu\)

矩是根据 [3] 和 [4] 实现的。

对于作为特殊情况的分布（如 Student 的 t），不建议依赖 genhyperbolic 的实现。 为了避免潜在的数值问题和出于性能原因，应使用特定分布的方法。

参考文献

[1]

O. Barndorff-Nielsen，“双曲分布和双曲上的分布”，《斯堪的纳维亚统计学杂志》，第 5(3) 卷，第 151-157 页，1978 年。 https://www.jstor.org/stable/4615705

[2]

Eberlein E., Prause K. (2002) 广义双曲模型：金融衍生品和风险度量。 Geman H., Madan D., Pliska S.R., Vorst T. (eds) 数学金融 - Bachelier Congress 2000。Springer Finance。 Springer, Berlin, Heidelberg. DOI:10.1007/978-3-662-12429-1_12

[3]

Scott, David J, Würtz, Diethelm, Dong, Christine 和 Tran, Thanh Tam, (2009)，广义双曲分布的矩，MPRA Paper，慕尼黑大学图书馆，德国，https://EconPapers.repec.org/RePEc:pra:mprapa:19081。

[4]

E. Eberlein 和 E. A. von Hammerstein。 广义双曲和逆高斯分布：过程的限制情况和近似。 FDM 预印本 80，2003 年 4 月。 弗莱堡大学。 https://freidok.uni-freiburg.de/fedora/objects/freidok:7974/datastreams/FILE1/content

示例

在您的浏览器中尝试！

>>> import numpy as np
>>> from scipy.stats import genhyperbolic
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

获取支持

>>> p, a, b = 0.5, 1.5, -0.5
>>> lb, ub = genhyperbolic.support(p, a, b)

计算前四个矩

>>> mean, var, skew, kurt = genhyperbolic.stats(p, a, b, moments='mvsk')

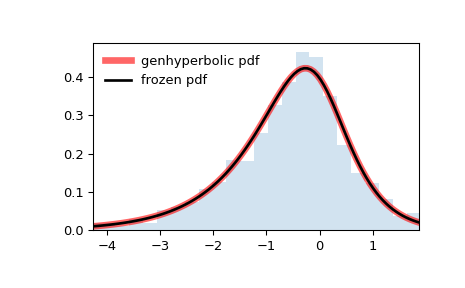
显示概率密度函数 (pdf)

>>> x = np.linspace(genhyperbolic.ppf(0.01, p, a, b),
...                 genhyperbolic.ppf(0.99, p, a, b), 100)
>>> ax.plot(x, genhyperbolic.pdf(x, p, a, b),
...        'r-', lw=5, alpha=0.6, label='genhyperbolic pdf')

或者，可以调用分布对象（作为函数）来固定形状、位置和尺度参数。 这会返回一个“冻结的” RV 对象，其中包含给定的固定参数。

冻结分布并显示冻结的 pdf

>>> rv = genhyperbolic(p, a, b)
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

检查 cdf 和 ppf 的准确性

>>> vals = genhyperbolic.ppf([0.001, 0.5, 0.999], p, a, b)
>>> np.allclose([0.001, 0.5, 0.999], genhyperbolic.cdf(vals, p, a, b))
True

生成随机数

>>> r = genhyperbolic.rvs(p, a, b, size=1000)

并比较直方图

>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2)
>>> ax.set_xlim([x[0], x[-1]])
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

返回在新标签页中打开