scipy.stats.

混合#

class scipy.stats.Mixture(components, *, weights=None)[source]#

混合分布的表示。

混合分布是以以下方式定义的随机变量的分布：首先，根据 weights 给出的概率，从 components 中选择一个随机变量，然后实现所选的随机变量。

参数:
componentsContinuousDistribution 的序列

ContinuousDistribution 的底层实例。所有实例都必须具有标量形状参数（如果有）；例如，在标量参数上评估的 pdf 必须返回一个标量。

weights浮点数序列，可选

选择每个随机变量的相应概率。必须是非负数且总和为 1。默认行为是对所有分量进行平均加权。

属性:
componentsContinuousDistribution 的序列

ContinuousDistribution 的底层实例。

weightsndarray

选择每个随机变量的相应概率。

方法

support()

随机变量的支持

sample([shape, rng, method])

从分布中随机取样。

moment([order, kind, method])

正整数阶的原始矩、中心矩或标准矩。

mean(*[, method])

均值（关于原点的原始一阶矩）

median(*[, method])

中位数（第 50 个百分位数）

mode(*[, method])

众数（最可能的值）

variance(*[, method])

方差（中心二阶矩）

standard_deviation(*[, method])

标准差（中心二阶矩的平方根）

skewness(*[, method])

偏度（标准化三阶矩）

kurtosis(*[, method])

峰度（标准化四阶矩）

pdf(x, /, *[, method])

概率密度函数

logpdf(x, /, *[, method])

概率密度函数的对数

cdf(x[, y, method])

累积分布函数

icdf(p, /, *[, method])

累积分布函数的逆函数。

ccdf(x[, y, method])

互补累积分布函数

iccdf(p, /, *[, method])

逆互补累积分布函数。

logcdf(x[, y, method])

累积分布函数的对数

ilogcdf(p, /, *[, method])

累积分布函数对数的逆函数。

logccdf(x[, y, method])

互补累积分布函数的对数

ilogccdf(p, /, *[, method])

互补累积分布函数对数的逆函数。

entropy(*[, method])

微分熵

说明

以下缩写用于整个文档。

  • PDF: 概率密度函数

  • CDF: 累积分布函数

  • CCDF: 互补 CDF

  • entropy: 微分熵

  • log-F: F 的对数 (例如 log-CDF)

  • inverse F: F 的逆函数 (例如逆 CDF)

参考

示例

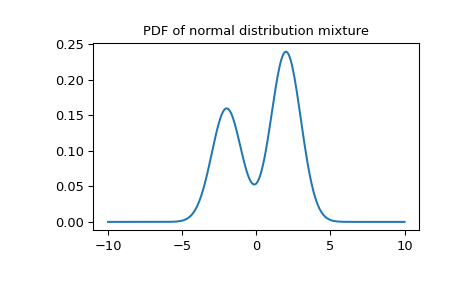
正态分布的混合

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> X1 = stats.Normal(mu=-2, sigma=1)
>>> X2 = stats.Normal(mu=2, sigma=1)
>>> mixture = stats.Mixture([X1, X2], weights=[0.4, 0.6])
>>> print(f'mean: {mixture.mean():.2f}, '
...       f'median: {mixture.median():.2f}, '
...       f'mode: {mixture.mode():.2f}')
mean: 0.40, median: 1.04, mode: 2.00
>>> x = np.linspace(-10, 10, 300)
>>> plt.plot(x, mixture.pdf(x))
>>> plt.title('PDF of normal distribution mixture')
>>> plt.show()
../../_images/scipy-stats-Mixture-1.png
在此页面上