scipy.special.nbdtrik#

scipy.special.nbdtrik(y, n, p, out=None) = <ufunc 'nbdtrik'>#

负二项式百分位数函数。

返回关于参数 k 的逆，即 y = nbdtr(k, n, p)（负二项式累积分布函数）。

参数:

yarray_like: 在 n 次成功之前，出现 k 次或更少失败的概率（浮点数）。
narray_like: 目标成功次数（正整数）。
parray_like: 单次事件中成功的概率（浮点数）。
outndarray, optional: 函数结果的输出数组（可选）

返回:

kscalar or ndarray: 允许的最大失败次数，使得 nbdtr(k, n, p) = y。

另请参阅

nbdtr: 负二项式的累积分布函数。
nbdtrc: 负二项式的生存函数。
nbdtri: 关于 p 的逆，即 nbdtr(k, n, p)。
nbdtrin: 关于 n 的逆，即 nbdtr(k, n, p)。
scipy.stats.nbinom: 负二项分布

注意

CDFLIB [1] Fortran 例程 cdfnbn 的包装器。

[2] 中的公式 26.5.26，

\[\sum_{j=k + 1}^\infty {{n + j - 1} \choose{j}} p^n (1 - p)^j = I_{1 - p}(k + 1, n),\]

用于将累积分布函数的计算简化为正则化不完全贝塔 \(I\)。

计算 k 涉及搜索能产生所需 y 值的数值。该搜索依赖于 y 随 k 的单调性。

参考文献

[1]

Barry Brown、James Lovato 和 Kathy Russell，CDFLIB：累积分布函数、逆函数和其他参数的 Fortran 例程库。

[2]

Milton Abramowitz 和 Irene A. Stegun 主编。《数学函数手册：公式、图表和数学表格》。纽约：Dover，1972。

示例

计算示例参数集的负二项式累积分布函数。

>>> import numpy as np
>>> from scipy.special import nbdtr, nbdtrik
>>> k, n, p = 5, 2, 0.5
>>> cdf_value = nbdtr(k, n, p)
>>> cdf_value
0.9375

验证 nbdtrik 恢复 k 的原始值。

>>> nbdtrik(cdf_value, n, p)
5.0

绘制不同参数集的函数。

>>> import matplotlib.pyplot as plt
>>> p_parameters = [0.2, 0.5, 0.7, 0.5]
>>> n_parameters = [30, 30, 30, 80]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(p_parameters, n_parameters, linestyles))
>>> cdf_vals = np.linspace(0, 1, 1000)
>>> fig, ax = plt.subplots(figsize=(8, 8))
>>> for parameter_set in parameters_list:
...     p, n, style = parameter_set
...     nbdtrik_vals = nbdtrik(cdf_vals, n, p)
...     ax.plot(cdf_vals, nbdtrik_vals, label=rf"$n={n},\ p={p}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_ylabel("$k$")
>>> ax.set_xlabel("$CDF$")
>>> ax.set_title("Negative binomial percentile function")
>>> plt.show()

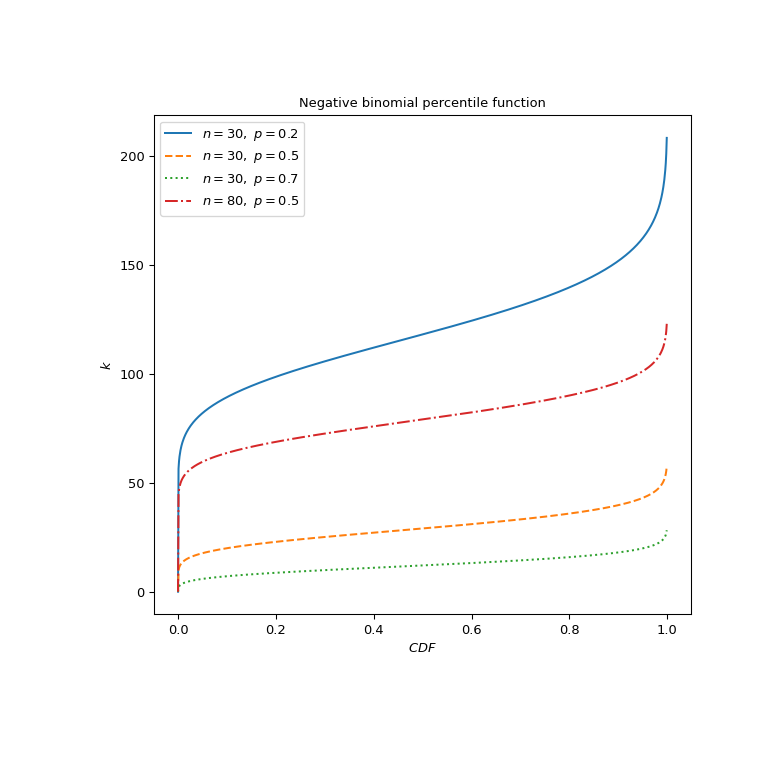
../../_images/scipy-special-nbdtrik-1_00_00.png

负二项分布也可用作 scipy.stats.nbinom。百分位数函数方法 ppf 返回 nbdtrik 向上取整后的结果

>>> from scipy.stats import nbinom
>>> q, n, p = 0.6, 5, 0.5
>>> nbinom.ppf(q, n, p), nbdtrik(q, n, p)
(5.0, 4.800428460273882)