scipy.special.nbdtri#

scipy.special.nbdtri(k, n, y, out=None) = <ufunc 'nbdtri'>#

返回关于参数 p 的 y = nbdtr(k, n, p) 的逆函数，即负二项累积分布函数。

参数:

karray_like: 允许的最大失败次数（非负整数）。
narray_like: 目标成功次数（正整数）。
yarray_like: 在 n 次成功之前，失败次数小于等于 k 的概率（浮点数）。
outndarray，可选: 函数结果的可选输出数组

返回:

p标量或 ndarray: 单次事件成功的概率（浮点数），使得 nbdtr(k, n, p) = y。

另请参阅

nbdtr: 负二项分布的累积分布函数。
nbdtrc: 负二项生存函数。
scipy.stats.nbinom: 负二项分布。
nbdtrik: 关于 nbdtr(k, n, p) 的 k 的逆函数。
nbdtrin: 关于 nbdtr(k, n, p) 的 n 的逆函数。
scipy.stats.nbinom: 负二项分布

说明

Cephes [1] 例程 nbdtri 的包装器。

负二项分布也以 scipy.stats.nbinom 的形式提供。与 scipy.stats.nbinom 的 ppf 方法相比，直接使用 nbdtri 可以提高性能。

参考文献

[1]

Cephes 数学函数库，http://www.netlib.org/cephes/

示例

nbdtri 是关于 p 的 nbdtr 的逆函数。在浮点误差范围内，以下等式成立：nbdtri(k, n, nbdtr(k, n, p))=p。

>>> import numpy as np
>>> from scipy.special import nbdtri, nbdtr
>>> k, n, y = 5, 10, 0.2
>>> cdf_val = nbdtr(k, n, y)
>>> nbdtri(k, n, cdf_val)
0.20000000000000004

通过为 y 提供 NumPy 数组或列表，计算 k=10 和 n=5 在多个点上的函数值。

>>> y = np.array([0.1, 0.4, 0.8])
>>> nbdtri(3, 5, y)
array([0.34462319, 0.51653095, 0.69677416])

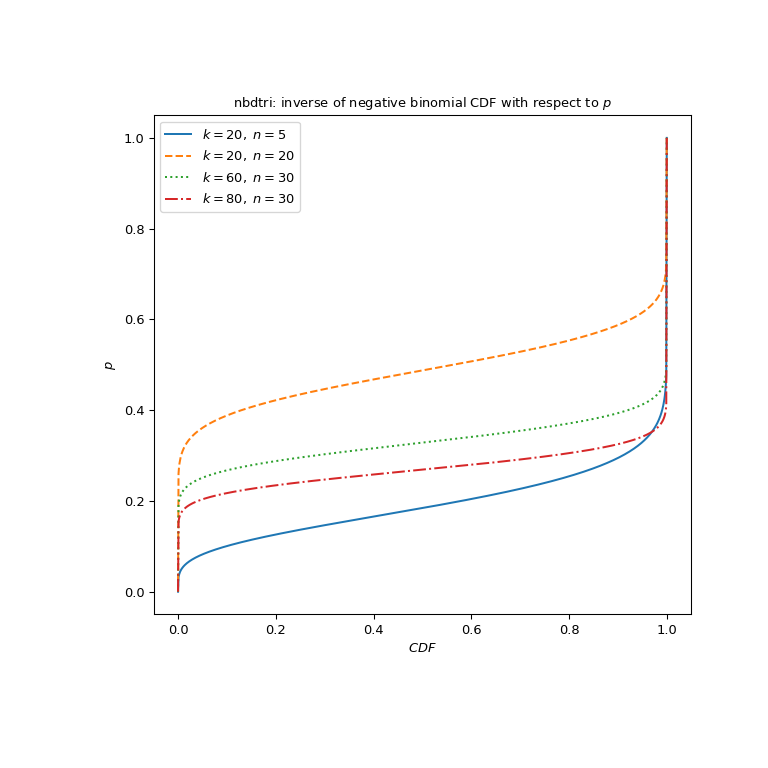
绘制三个不同参数集的函数图像。

>>> import matplotlib.pyplot as plt
>>> n_parameters = [5, 20, 30, 30]
>>> k_parameters = [20, 20, 60, 80]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(n_parameters, k_parameters, linestyles))
>>> cdf_vals = np.linspace(0, 1, 1000)
>>> fig, ax = plt.subplots(figsize=(8, 8))
>>> for parameter_set in parameters_list:
...     n, k, style = parameter_set
...     nbdtri_vals = nbdtri(k, n, cdf_vals)
...     ax.plot(cdf_vals, nbdtri_vals, label=rf"$k={k},\ n={n}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_ylabel("$p$")
>>> ax.set_xlabel("$CDF$")
>>> title = "nbdtri: inverse of negative binomial CDF with respect to $p$"
>>> ax.set_title(title)
>>> plt.show()

../../_images/scipy-special-nbdtri-1_00_00.png

通过为 k、n 和 p 提供兼容广播的形状的数组，nbdtri 可以评估不同的参数集。这里，我们计算三个不同的 k 在四个位置 p 的函数值，得到一个 3x4 的数组。

>>> k = np.array([[5], [10], [15]])
>>> y = np.array([0.3, 0.5, 0.7, 0.9])
>>> k.shape, y.shape
((3, 1), (4,))

>>> nbdtri(k, 5, y)
array([[0.37258157, 0.45169416, 0.53249956, 0.64578407],
       [0.24588501, 0.30451981, 0.36778453, 0.46397088],
       [0.18362101, 0.22966758, 0.28054743, 0.36066188]])