散点数据插值 (griddata)#
假设您有多维数据,例如,对于一个底层函数 \(f(x, y)\),您只知道非规则网格上点 (x[i], y[i]) 的值。
假设我们想对 2D 函数进行插值
>>> import numpy as np
>>> def func(x, y):
... return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
在 [0, 1]x[0, 1] 上的网格中
>>> grid_x, grid_y = np.meshgrid(np.linspace(0, 1, 100),
... np.linspace(0, 1, 200), indexing='ij')
但我们只知道它在 1000 个数据点上的值
>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])
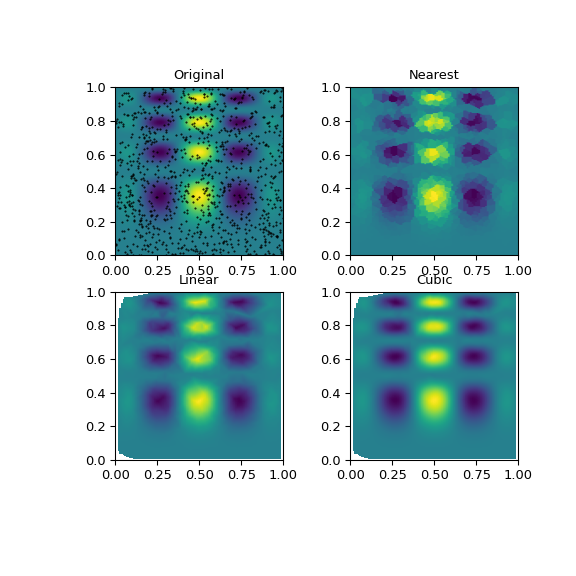
这可以通过 griddata 完成 —— 下面,我们尝试所有插值方法
>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')
可以看出,所有方法都在某种程度上再现了精确结果,但对于这种平滑函数,分段三次插值器给出了最佳结果(黑点显示了正在插值的数据)
>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.plot(points[:, 0], points[:, 1], 'k.', ms=1) # data
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()
对于每种插值方法,此函数都委托给相应的类对象 —— 这些类也可以直接使用 —— 分别是 NearestNDInterpolator、LinearNDInterpolator 和用于 2D 分段三次插值的 CloughTocher2DInterpolator。
所有这些插值方法都依赖于使用封装在 scipy.spatial 中的 QHull 库对数据进行三角剖分。
注意
griddata 基于三角剖分,因此适用于非结构化、散点数据。如果您的数据位于完整网格上,则 griddata 函数——尽管有其名称——并非正确的工具。请改用 RegularGridInterpolator。
注意
如果输入数据的维度单位不相称且相差多个数量级,则插值器可能会产生数值伪影。在插值之前考虑重新缩放数据,或在 griddata 中使用 rescale=True 关键字参数。
使用径向基函数进行平滑/插值#
径向基函数可用于 N 维散点数据的平滑/插值,但对于观测数据范围之外的外推应谨慎使用。
一维示例#
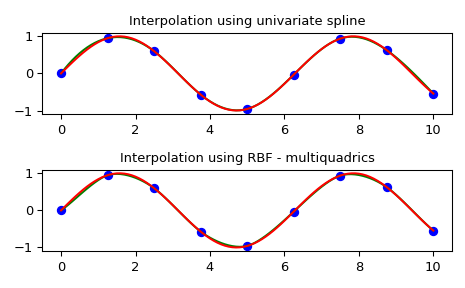
此示例比较了 RBFInterpolator 和 UnivariateSpline 类在 scipy.interpolate 模块中的用法。
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator, InterpolatedUnivariateSpline
>>> import matplotlib.pyplot as plt
>>> # setup data
>>> x = np.linspace(0, 10, 9).reshape(-1, 1)
>>> y = np.sin(x)
>>> xi = np.linspace(0, 10, 101).reshape(-1, 1)
>>> # use fitpack2 method
>>> ius = InterpolatedUnivariateSpline(x, y)
>>> yi = ius(xi)
>>> fix, (ax1, ax2) = plt.subplots(2, 1)
>>> ax1.plot(x, y, 'bo')
>>> ax1.plot(xi, yi, 'g')
>>> ax1.plot(xi, np.sin(xi), 'r')
>>> ax1.set_title('Interpolation using univariate spline')
>>> # use RBF method
>>> rbf = RBFInterpolator(x, y)
>>> fi = rbf(xi)
>>> ax2.plot(x, y, 'bo')
>>> ax2.plot(xi, fi, 'g')
>>> ax2.plot(xi, np.sin(xi), 'r')
>>> ax2.set_title('Interpolation using RBF - multiquadrics')
>>> plt.tight_layout()
>>> plt.show()
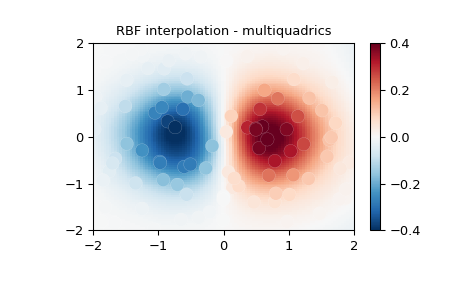
二维示例#
此示例展示了如何插值散点 2D 数据
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator
>>> import matplotlib.pyplot as plt
>>> # 2-d tests - setup scattered data
>>> rng = np.random.default_rng()
>>> xy = rng.random((100, 2))*4.0-2.0
>>> z = xy[:, 0]*np.exp(-xy[:, 0]**2-xy[:, 1]**2)
>>> edges = np.linspace(-2.0, 2.0, 101)
>>> centers = edges[:-1] + np.diff(edges[:2])[0] / 2.
>>> x_i, y_i = np.meshgrid(centers, centers)
>>> x_i = x_i.reshape(-1, 1)
>>> y_i = y_i.reshape(-1, 1)
>>> xy_i = np.concatenate([x_i, y_i], axis=1)
>>> # use RBF
>>> rbf = RBFInterpolator(xy, z, epsilon=2)
>>> z_i = rbf(xy_i)
>>> # plot the result
>>> fig, ax = plt.subplots()
>>> X_edges, Y_edges = np.meshgrid(edges, edges)
>>> lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
>>> mapping = ax.pcolormesh(
... X_edges, Y_edges, z_i.reshape(100, 100),
... shading='flat', **lims
... )
>>> ax.scatter(xy[:, 0], xy[:, 1], 100, z, edgecolor='w', lw=0.1, **lims)
>>> ax.set(
... title='RBF interpolation - multiquadrics',
... xlim=(-2, 2),
... ylim=(-2, 2),
... )
>>> fig.colorbar(mapping)