scipy.interpolate.

RBFInterpolator#

class scipy.interpolate.RBFInterpolator(y, d, neighbors=None, smoothing=0.0, kernel='thin_plate_spline', epsilon=None, degree=None)[source]#

N ≥ 1 维径向基函数插值器。

参数:
y(npoints, ndims) 类数组

数据点坐标的二维数组。

d(npoints, …) 类数组

y 处数据值的 N 维数组。 d 沿第一轴的长度必须等于 y 的长度。与某些插值器不同，插值轴无法更改。

neighbors整型, 可选

如果指定，每个评估点的插值结果将仅使用此数量的最近数据点计算。默认情况下使用所有数据点。

smoothing浮点型或 (npoints, ) 类数组, 可选

平滑参数。当此参数设置为 0 时，插值器完美拟合数据。对于较大值，插值器接近指定阶数多项式的最小二乘拟合。默认值为 0。

kernel字符串, 可选

RBF 类型。应为以下之一：

  • ‘linear’ : -r

  • ‘thin_plate_spline’ : r**2 * log(r)

  • ‘cubic’ : r**3

  • ‘quintic’ : -r**5

  • ‘multiquadric’ : -sqrt(1 + r**2)

  • ‘inverse_multiquadric’ : 1/sqrt(1 + r**2)

  • ‘inverse_quadratic’ : 1/(1 + r**2)

  • ‘gaussian’ : exp(-r**2)

默认值为 ‘thin_plate_spline’。

epsilon浮点型, 可选

用于缩放 RBF 输入的形状参数。如果 kernel 是 ‘linear’、‘thin_plate_spline’、‘cubic’ 或 ‘quintic’，则此参数默认为 1 且可以忽略，因为它与缩放平滑参数具有相同的效果。否则，必须指定此参数。

degree整型, 可选

附加多项式的阶数。对于某些 RBF，如果多项式阶数过小，则插值结果可能不是适定的。这些 RBF 及其对应的最小阶数如下：

  • ‘multiquadric’ : 0

  • ‘linear’ : 0

  • ‘thin_plate_spline’ : 1

  • ‘cubic’ : 1

  • ‘quintic’ : 2

默认值为 kernel 的最小阶数，如果没有最小阶数则为 0。设置为 -1 表示不附加多项式。

方法

__call__(x)

评估 x 处的插值结果。

另请参阅

NearestNDInterpolator
LinearNDInterpolator
CloughTocher2DInterpolator

备注

RBF 是 N 维空间中的一个标量值函数，其在 \(x\) 处的值可以表示为 \(r=||x - c||\)，其中 \(c\) 是 RBF 的中心。

对于数据值向量 \(d\)（来自位置 \(y\)），RBF 插值器是中心位于 \(y\) 的 RBF 的线性组合，再加上一个指定阶数的多项式。RBF 插值器表示为

\[f(x) = K(x, y) a + P(x) b,\]

其中 \(K(x, y)\) 是以 \(y\) 为中心的 RBF 矩阵，并在点 \(x\) 处评估； \(P(x)\) 是单项式矩阵，它构成指定阶数的多项式，并在 \(x\) 处评估。系数 \(a\) 和 \(b\) 是线性方程组的解：

\[(K(y, y) + \lambda I) a + P(y) b = d\]

和

\[P(y)^T a = 0,\]

其中 \(\lambda\) 是一个非负平滑参数，控制我们拟合数据的程度。当平滑参数为 0 时，数据被精确拟合。

如果满足以下要求，上述系统是唯一可解的：

  • \(P(y)\) 必须具有满列秩。当 degree 为 -1 或 0 时，\(P(y)\) 始终具有满列秩。当 degree 为 1 时，如果数据点位置不都是共线（N=2）、共面（N=3）等，则 \(P(y)\) 具有满列秩。

  • 如果 kernel 是 ‘multiquadric’、‘linear’、‘thin_plate_spline’、‘cubic’ 或 ‘quintic’，则 degree 不得低于上面列出的最小值。

  • 如果 smoothing 为 0，则每个数据点位置必须是唯一的。

当使用非尺度不变的 RBF（‘multiquadric’、‘inverse_multiquadric’、‘inverse_quadratic’ 或 ‘gaussian’）时，必须选择合适的形状参数（例如，通过交叉验证）。形状参数值越小，RBF 越宽。当形状参数过小时，问题可能变得病态或奇异。

求解 RBF 插值系数所需的内存随数据点数量呈二次方增加，这在插值超过大约一千个数据点时可能变得不切实际。为了克服大型插值问题的内存限制，可以指定 neighbors 参数，以便仅使用最近的数据点为每个评估点计算 RBF 插值。

版本 1.7.0 新增。

参考文献

[1]

Fasshauer, G., 2007. Meshfree Approximation Methods with Matlab. World Scientific Publishing Co.

[3]

Wahba, G., 1990. Spline Models for Observational Data. SIAM.

示例

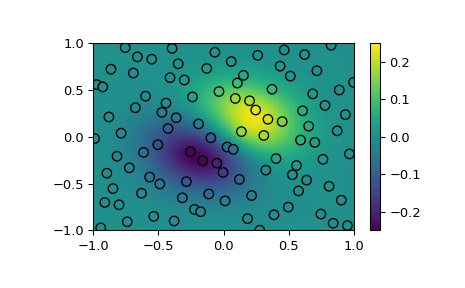
演示将二维散点数据插值到网格中。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import RBFInterpolator
>>> from scipy.stats.qmc import Halton

>>> rng = np.random.default_rng()
>>> xobs = 2*Halton(2, seed=rng).random(100) - 1
>>> yobs = np.sum(xobs, axis=1)*np.exp(-6*np.sum(xobs**2, axis=1))

>>> xgrid = np.mgrid[-1:1:50j, -1:1:50j]
>>> xflat = xgrid.reshape(2, -1).T
>>> yflat = RBFInterpolator(xobs, yobs)(xflat)
>>> ygrid = yflat.reshape(50, 50)

>>> fig, ax = plt.subplots()
>>> ax.pcolormesh(*xgrid, ygrid, vmin=-0.25, vmax=0.25, shading='gouraud')
>>> p = ax.scatter(*xobs.T, c=yobs, s=50, ec='k', vmin=-0.25, vmax=0.25)
>>> fig.colorbar(p)
>>> plt.show()
../../_images/scipy-interpolate-RBFInterpolator-1.png
本页内容