scipy.stats.qmc.

PoissonDisk#

class scipy.stats.qmc.PoissonDisk(d, *, radius=0.05, hypersphere='volume', ncandidates=30, optimization=None, rng=None, l_bounds=None, u_bounds=None)[source]#

泊松盘采样。

参数:
dint

参数空间的维度。

radiusfloat

在采样新候选项时，点之间要保持的最小距离。

hypersphere{“volume”, “surface”}, optional

用于生成最终样本中要添加的潜在候选项的采样策略。默认为“volume”。

  • volume: 原始 Bridson 算法，如 [1] 中所述。 新候选项在超球体内采样。

  • surface: 仅对超球体的表面进行采样。

ncandidatesint

每次迭代采样的候选项数量。 更多候选项会导致更密集的采样，因为每次迭代可以接受更多候选项。

optimization{None, “random-cd”, “lloyd”}, optional

是否使用优化方案来提高采样后的质量。 请注意，这是一个后处理步骤，不能保证样本的所有属性都得到保留。 默认为 None。

  • random-cd: 坐标的随机排列以降低中心差异。 基于中心差异的最佳样本会不断更新。 与使用其他差异度量相比，基于中心差异的采样在 2D 和 3D 子投影中显示出更好的空间填充鲁棒性。

  • lloyd: 使用修改后的 Lloyd-Max 算法扰动样本。 该过程收敛到等间距的样本。

1.10.0 版本新增。

rngnumpy.random.Generator, optional

伪随机数生成器状态。 当 rng 为 None 时，将使用来自操作系统的熵创建一个新的 numpy.random.Generator。 除 numpy.random.Generator 之外的类型将传递给 numpy.random.default_rng 以实例化 Generator。

1.15.0 版本更改: 作为从使用 numpy.random.RandomState 过渡到 numpy.random.Generator 的 SPEC-007 过渡的一部分，此关键字已从 seed 更改为 rng。 在过渡期间，这两个关键字将继续工作，尽管一次只能指定一个。 在过渡期之后，使用 seed 关键字的函数调用将发出警告。 在弃用期之后，将删除 seed 关键字。

l_bounds, u_boundsarray_like (d,)

目标样本数据的下限和上限。

方法

fast_forward(n)

将序列快进 n 个位置。

fill_space()

在间隔 [l_bounds, u_bounds] 中绘制 n 个样本。

integers(l_bounds, *[, u_bounds, n, ...])

从 l_bounds （包括）到 u_bounds （不包括）绘制 n 个整数，或者如果 endpoint=True，则从 l_bounds （包括）到 u_bounds （包括）。

random([n, workers])

在半开区间 [0, 1) 中绘制 n。

reset()

将引擎重置为基本状态。

注释

泊松盘采样是一种迭代采样策略。 从种子样本开始，在种子周围的超球体中采样 ncandidates。 拒绝低于某个 radius 或在域外的候选项。 新样本添加到样本种子池中。 当池为空或达到所需样本数时，该过程停止。

样本可以包含的最大点数与 radius 直接相关。 随着空间维度的增加，更高的半径会进一步分散点，并有助于克服维度诅咒。 有关更多详细信息，请参阅 拟蒙特卡罗教程。

警告

由于其迭代性质和内存需求，该算法更适合低维度和采样大小。 选择具有高维度的小半径意味着该空间可能包含比使用低维度或更大半径更多的样本。

一些代码取自 [2]，原始作者 Shamis 在 2021 年 3 月 31 日给予了书面同意，允许在 3 条款 BSD 下在 SciPy 中免费使用。

参考文献

[1]

Robert Bridson，“任意维度中的快速泊松盘采样”。 SIGGRAPH，2007 年。

示例

使用 0.2 的 radius 生成 2D 样本。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from matplotlib.collections import PatchCollection
>>> from scipy.stats import qmc
>>>
>>> rng = np.random.default_rng()
>>> radius = 0.2
>>> engine = qmc.PoissonDisk(d=2, radius=radius, rng=rng)
>>> sample = engine.random(20)

可视化 2D 样本并显示没有点比 radius 更接近。 radius/2 用于可视化非相交的圆。 如果两个样本彼此相距正好 radius，则它们的 radius/2 半径圆将接触。

>>> fig, ax = plt.subplots()
>>> _ = ax.scatter(sample[:, 0], sample[:, 1])
>>> circles = [plt.Circle((xi, yi), radius=radius/2, fill=False)
...            for xi, yi in sample]
>>> collection = PatchCollection(circles, match_original=True)
>>> ax.add_collection(collection)
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> plt.show()
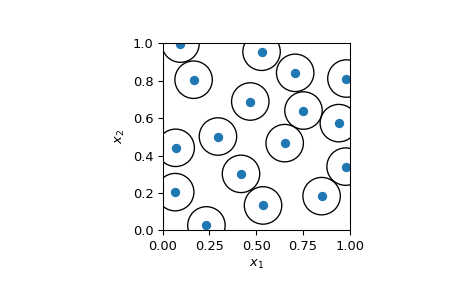
../../_images/scipy-stats-qmc-PoissonDisk-1_00_00.png

这种可视化可以看作是圆形填充：我们可以在空间中放置多少个圆。 这是一个 np-hard 问题。 方法 fill_space 可用于添加样本，直到无法添加更多样本。 这是一个难题，可能需要手动调整参数。 请注意维度：随着维度增加，填充空间所需的样本数量呈指数增长（维度诅咒）。

在此页上