拟蒙特卡罗#
在讨论拟蒙特卡罗(QMC)之前,先快速介绍一下蒙特卡罗(MC)。MC 方法,或称 MC 实验,是一大类计算算法,它们依赖重复随机抽样来获得数值结果。其基本概念是利用随机性来解决原则上可能是确定性的问题。它们常用于物理和数学问题,在难以或不可能使用其他方法时最有用。MC 方法主要用于三类问题:优化、数值积分以及从概率分布中生成样本。
生成具有特定属性的随机数是一个比听起来更复杂的问题。简单的 MC 方法旨在以独立同分布(IID)的方式采样点。但生成多组随机点可能会产生截然不同的结果。
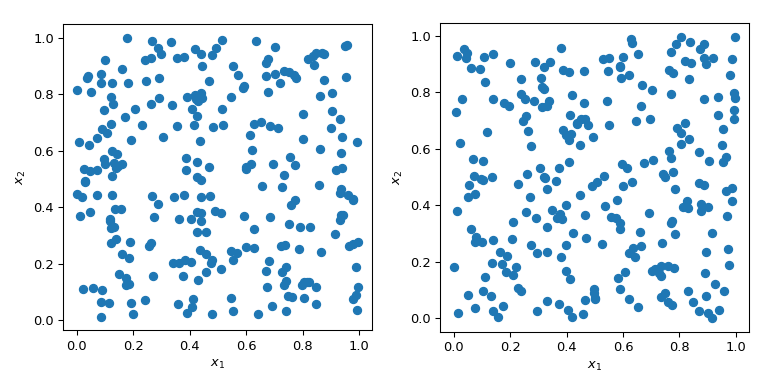
在上述图中两种情况下,点的生成都是随机的,没有关于先前抽取点的任何信息。显然,空间中的某些区域未被探索——这可能在模拟中导致问题,因为特定的点集可能会引发完全不同的行为。
MC 的一个巨大优势是它具有已知的收敛特性。让我们来看看 5 维平方和的平均值
其中 \(x_j \sim \mathcal{U}(0,1)\)。它有一个已知的平均值,\(\mu = 5/3+5(5-1)/4\)。使用 MC 采样,我们可以数值计算该平均值,并且近似误差遵循 \(O(n^{-1/2})\) 的理论收敛速度。
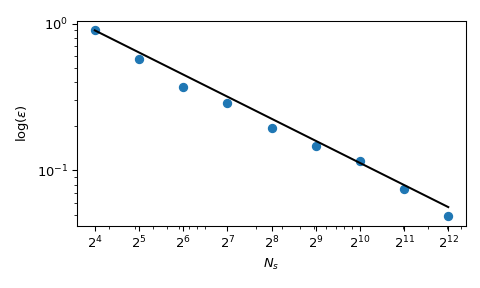
尽管收敛性得到了保证,但实践者倾向于希望探索过程更具确定性。对于普通的 MC,可以使用种子来实现可重复的过程。但是固定种子会破坏收敛性:某个给定的种子可能适用于某一类问题,但在另一类问题上则会失效。
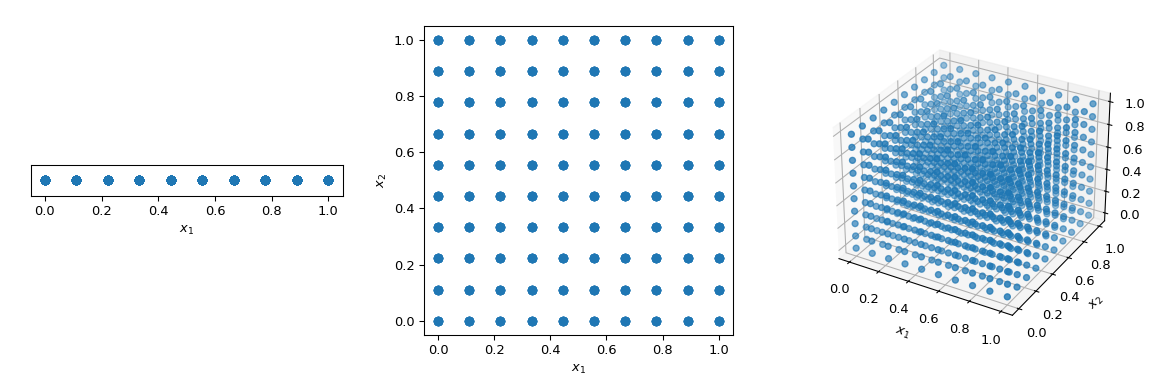
通常以确定性方式遍历空间的方法是使用一个跨越所有参数维度的规则网格,也称为饱和设计。让我们考虑单位超立方体,所有边界范围从 0 到 1。现在,如果点之间的距离为 0.1,则填充单位区间所需的点数为 10。在 2 维超立方体中,相同的间距将需要 100 个点,而在 3 维中则需要 1,000 个点。随着维度数量的增加,填充空间所需的实验数量随着空间维度的增加呈指数级增长。这种指数增长被称为“维度诅咒”。
>>> import numpy as np
>>> disc = 10
>>> x1 = np.linspace(0, 1, disc)
>>> x2 = np.linspace(0, 1, disc)
>>> x3 = np.linspace(0, 1, disc)
>>> x1, x2, x3 = np.meshgrid(x1, x2, x3)
为了缓解这个问题,QMC 方法应运而生。它们是确定性的,对空间有很好的覆盖,其中一些方法可以继续生成并保持良好的特性。与 MC 方法的主要区别在于,QMC 方法中的点不是独立同分布的(IID),而是“知道”先前的点。因此,有些方法也被称为序列。
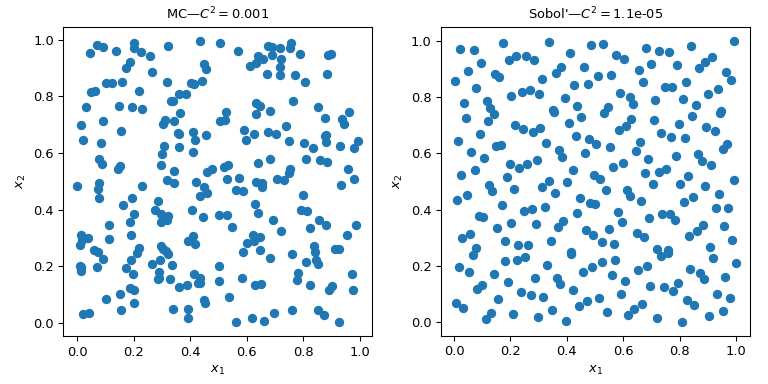
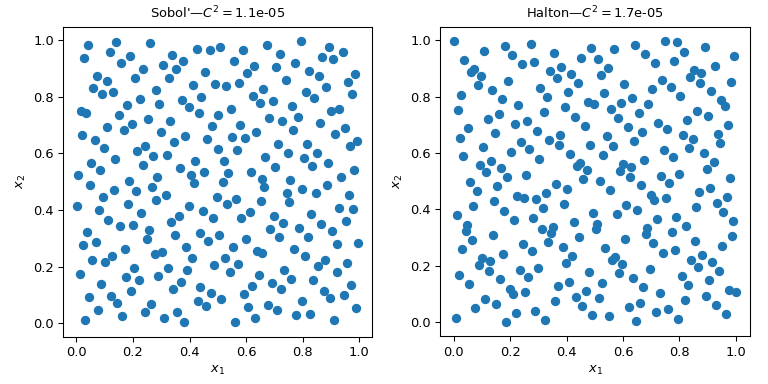
此图显示了两组 256 个点。左侧的设计是普通的 MC,而右侧的设计是使用 Sobol’ 方法的 QMC 设计。我们清楚地看到 QMC 版本更均匀。这些点在边界附近采样更好,并且聚类或间隙更少。
评估均匀性的一种方法是使用一种称为差异的度量。在这里,Sobol’ 点的差异优于粗略的 MC。
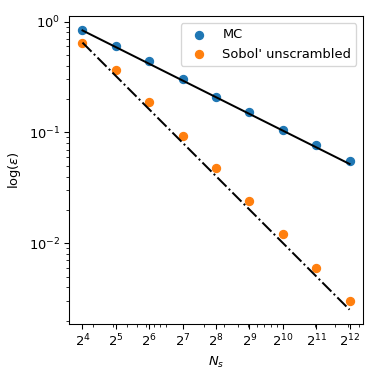
回到平均值的计算,QMC 方法在误差方面也具有更好的收敛速度。对于此函数,它们可以达到 \(O(n^{-1})\) 的速度,对于非常平滑的函数甚至可以达到更好的速度。此图显示 Sobol’ 方法的收敛速度为 \(O(n^{-1})\)
有关更多数学细节,请参阅 scipy.stats.qmc 的文档。
计算差异#
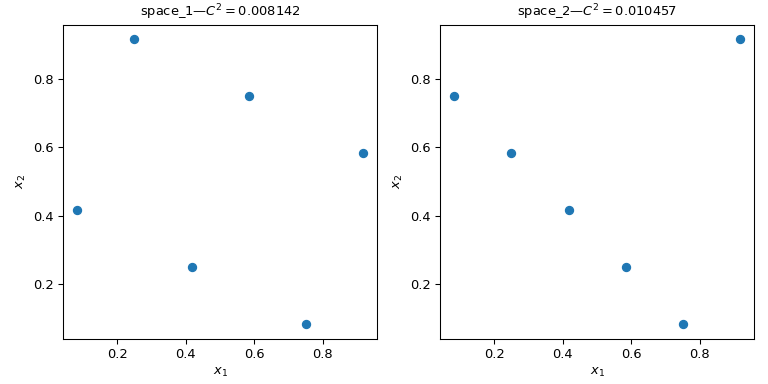
让我们考虑两组点。从下图可以看出,左侧的设计比右侧的设计覆盖了更多的空间。这可以使用 scipy.stats.qmc.discrepancy 度量来量化。差异越小,样本越均匀。
>>> import numpy as np
>>> from scipy.stats import qmc
>>> space_1 = np.array([[1, 3], [2, 6], [3, 2], [4, 5], [5, 1], [6, 4]])
>>> space_2 = np.array([[1, 5], [2, 4], [3, 3], [4, 2], [5, 1], [6, 6]])
>>> l_bounds = [0.5, 0.5]
>>> u_bounds = [6.5, 6.5]
>>> space_1 = qmc.scale(space_1, l_bounds, u_bounds, reverse=True)
>>> space_2 = qmc.scale(space_2, l_bounds, u_bounds, reverse=True)
>>> qmc.discrepancy(space_1)
0.008142039609053464
>>> qmc.discrepancy(space_2)
0.010456854423869011
使用 QMC 引擎#
已实现了多种 QMC 采样器/引擎。这里我们介绍两种最常用的 QMC 方法:scipy.stats.qmc.Sobol 和 scipy.stats.qmc.Halton 序列。
"""Sobol' and Halton sequences."""
from scipy.stats import qmc
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
n_sample = 256
dim = 2
sample = {}
# Sobol'
engine = qmc.Sobol(d=dim, seed=rng)
sample["Sobol'"] = engine.random(n_sample)
# Halton
engine = qmc.Halton(d=dim, seed=rng)
sample["Halton"] = engine.random(n_sample)
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
for i, kind in enumerate(sample):
axs[i].scatter(sample[kind][:, 0], sample[kind][:, 1])
axs[i].set_aspect('equal')
axs[i].set_xlabel(r'$x_1$')
axs[i].set_ylabel(r'$x_2$')
axs[i].set_title(f'{kind}—$C^2 = ${qmc.discrepancy(sample[kind]):.2}')
plt.tight_layout()
plt.show()
警告
QMC 方法需要特别注意,用户必须阅读文档以避免常见的陷阱。例如,Sobol’ 要求点数是 2 的幂。此外,稀疏化、“烧入”(burning)或其他点选择方式可能会破坏序列的属性,导致生成的效果不如 MC 的点集。
QMC 引擎是状态感知的。这意味着你可以继续生成序列、跳过一些点或重置它。让我们从 scipy.stats.qmc.Halton 中取 5 个点。然后请求第二组 5 个点
>>> from scipy.stats import qmc
>>> engine = qmc.Halton(d=2)
>>> engine.random(5)
array([[0.22166437, 0.07980522], # random
[0.72166437, 0.93165708],
[0.47166437, 0.41313856],
[0.97166437, 0.19091633],
[0.01853937, 0.74647189]])
>>> engine.random(5)
array([[0.51853937, 0.52424967], # random
[0.26853937, 0.30202745],
[0.76853937, 0.857583 ],
[0.14353937, 0.63536078],
[0.64353937, 0.01807683]])
现在我们重置序列。请求 5 个点将得到相同的前 5 个点
>>> engine.reset()
>>> engine.random(5)
array([[0.22166437, 0.07980522], # random
[0.72166437, 0.93165708],
[0.47166437, 0.41313856],
[0.97166437, 0.19091633],
[0.01853937, 0.74647189]])
然后我们推进序列以获得相同的第二组 5 个点
>>> engine.reset()
>>> engine.fast_forward(5)
>>> engine.random(5)
array([[0.51853937, 0.52424967], # random
[0.26853937, 0.30202745],
[0.76853937, 0.857583 ],
[0.14353937, 0.63536078],
[0.64353937, 0.01807683]])
注意
默认情况下,scipy.stats.qmc.Sobol 和 scipy.stats.qmc.Halton 都是打乱的(scrambled)。这样收敛特性更好,并能防止在高维空间中出现条纹或明显的点模式。没有实际理由不使用打乱版本。
创建 QMC 引擎,即继承 QMCEngine#
要创建自己的 scipy.stats.qmc.QMCEngine,需要定义一些方法。下面是一个封装 numpy.random.Generator 的例子。
>>> import numpy as np
>>> from scipy.stats import qmc
>>> class RandomEngine(qmc.QMCEngine):
... def __init__(self, d, seed=None):
... super().__init__(d=d, seed=seed)
... self.rng = np.random.default_rng(self.rng_seed)
...
...
... def _random(self, n=1, *, workers=1):
... return self.rng.random((n, self.d))
...
...
... def reset(self):
... self.rng = np.random.default_rng(self.rng_seed)
... self.num_generated = 0
... return self
...
...
... def fast_forward(self, n):
... self.random(n)
... return self
然后我们像使用其他 QMC 引擎一样使用它
>>> engine = RandomEngine(2)
>>> engine.random(5)
array([[0.22733602, 0.31675834], # random
[0.79736546, 0.67625467],
[0.39110955, 0.33281393],
[0.59830875, 0.18673419],
[0.67275604, 0.94180287]])
>>> engine.reset()
>>> engine.random(5)
array([[0.22733602, 0.31675834], # random
[0.79736546, 0.67625467],
[0.39110955, 0.33281393],
[0.59830875, 0.18673419],
[0.67275604, 0.94180287]])
QMC 使用指南#
QMC 有其规则!务必阅读文档,否则可能无法获得优于 MC 的效果。
如果需要**精确地** \(2^m\) 个点,请使用
scipy.stats.qmc.Sobol。scipy.stats.qmc.Halton允许采样或跳过任意数量的点。这代价是收敛速度比 Sobol’ 慢。切勿移除序列的起始点。这会破坏其特性。
打乱(Scrambling)总是更好的。
如果使用基于 LHS 的方法,则无法在不丧失 LHS 特性的情况下添加点。(有一些方法可以做到,但这尚未实现。)