scipy.stats.

linregress#

scipy.stats.linregress(x, y, alternative='two-sided', *, axis=0, nan_policy='propagate', keepdims=False)[source]#

计算两组测量的线性最小二乘回归。

参数:
x, yarray_like

两组测量值。两个数组都应具有相同的长度 N。

alternative{‘two-sided’, ‘less’, ‘greater’}, optional

定义备择假设。 默认为“two-sided”。 以下选项可用

  • ‘two-sided’：回归线的斜率不为零

  • ‘less’：回归线的斜率小于零

  • ‘greater’：回归线的斜率大于零

1.7.0 版本中新增。

axisint or None, default: 0

如果为 int，则为沿其计算统计信息的输入的轴。输入的每个轴切片（例如，行）的统计信息将显示在输出的相应元素中。如果为 None，则在计算统计信息之前将展开输入。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入 NaN。

  • propagate：如果在计算统计信息的轴切片（例如，行）中存在 NaN，则输出的相应条目将为 NaN。

  • omit：执行计算时将忽略 NaN。如果沿其计算统计信息的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

  • raise：如果存在 NaN，将引发 ValueError。

keepdimsbool, default: False

如果将其设置为 True，则缩减的轴将作为大小为 1 的维度保留在结果中。使用此选项，结果将针对输入数组正确广播。

返回值:
resultLinregressResult 实例

返回值是一个具有以下属性的对象

slopefloat

回归线的斜率。

interceptfloat

回归线的截距。

rvaluefloat

Pearson 相关系数。 rvalue 的平方等于决定系数。

pvaluefloat

假设检验的 p 值，其零假设是斜率为零，使用 Wald 检验和检验统计量的 t 分布。有关备择假设，请参阅上面的 alternative。

stderrfloat

估计斜率（梯度）的标准误差，在残差正态性的假设下。

intercept_stderrfloat

估计截距的标准误差，在残差正态性的假设下。

参见

scipy.optimize.curve_fit

使用非线性最小二乘法将函数拟合到数据。

scipy.optimize.leastsq

最小化一组方程的平方和。

注释

为了与旧版本的 SciPy 兼容，返回值的作用类似于长度为 5 的 namedtuple，其字段为 slope、intercept、rvalue、pvalue 和 stderr，因此您可以继续编写

slope, intercept, r, p, se = linregress(x, y)

但是，使用该样式，截距的标准误差不可用。 要访问所有计算值，包括截距的标准误差，请将返回值用作具有属性的对象，例如

result = linregress(x, y)
print(result.intercept, result.intercept_stderr)

从 SciPy 1.9 开始，np.matrix 输入（不建议用于新代码）会在执行计算之前转换为 np.ndarray。 在这种情况下，输出将是标量或适当形状的 np.ndarray，而不是 2D np.matrix。 同样，虽然会忽略屏蔽数组的屏蔽元素，但输出将是标量或 np.ndarray，而不是 mask=False 的屏蔽数组。

示例

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> rng = np.random.default_rng()

生成一些数据

>>> x = rng.random(10)
>>> y = 1.6*x + rng.random(10)

执行线性回归

>>> res = stats.linregress(x, y)

决定系数（R 平方）

>>> print(f"R-squared: {res.rvalue**2:.6f}")
R-squared: 0.717533

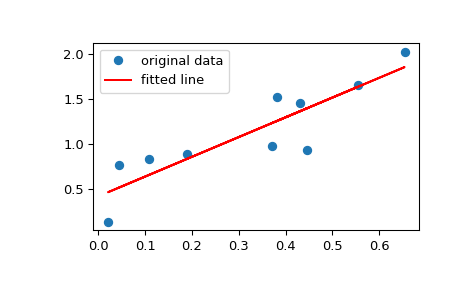
绘制数据以及拟合线

>>> plt.plot(x, y, 'o', label='original data')
>>> plt.plot(x, res.intercept + res.slope*x, 'r', label='fitted line')
>>> plt.legend()
>>> plt.show()
../../_images/scipy-stats-linregress-1_00_00.png

计算斜率和截距的 95% 置信区间

>>> # Two-sided inverse Students t-distribution
>>> # p - probability, df - degrees of freedom
>>> from scipy.stats import t
>>> tinv = lambda p, df: abs(t.ppf(p/2, df))

>>> ts = tinv(0.05, len(x)-2)
>>> print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}")
slope (95%): 1.453392 +/- 0.743465
>>> print(f"intercept (95%): {res.intercept:.6f}"
...       f" +/- {ts*res.intercept_stderr:.6f}")
intercept (95%): 0.616950 +/- 0.544475
在本页中