scipy.stats.

fit

scipy.stats.fit(dist, data, bounds=None, *, guess=None, method='mle', optimizer=<function differential_evolution>)

将离散或连续分布拟合到数据

给定分布、数据和分布参数的界限，返回参数的最大似然估计值。

参数:

distscipy.stats.rv_continuous 或 scipy.stats.rv_discrete

表示要拟合到数据的分布的对象。

data一维 array_like

要将分布拟合到的数据。 如果数据包含任何 np.nan、np.inf 或 -np.inf，则 fit 方法将引发 ValueError。

boundsdict 或元组序列，可选

如果是一个字典，则每个键是分布的参数名称，对应的值是一个包含该参数下限和上限的元组。如果分布仅为该参数的有限值范围定义，则不需要该参数的条目；例如，某些分布的参数必须位于区间 [0, 1] 上。参数 location (loc) 和 scale (scale) 的界限是可选的；默认情况下，它们分别固定为 0 和 1。

如果是一个序列，则元素 i 是一个包含分布的第 i 个参数的下限和上限的元组。在这种情况下，必须提供所有分布形状参数的界限。可选地，location 和 scale 的界限可以跟在分布形状参数之后。

如果要固定形状（例如，如果已知），则下限和上限可以相等。如果用户提供的下限或上限超出定义分布的域的范围，则分布域的界限将替换用户提供的值。类似地，必须为整数的参数将被约束为用户提供的界限内的整数值。

guessdict 或 array_like，可选

如果是一个字典，则每个键是分布的参数名称，对应的值是该参数值的猜测值。

如果是一个序列，则元素 i 是分布的第 i 个参数的猜测值。在这种情况下，必须提供所有分布形状参数的猜测值。

如果未提供 guess，则决策变量的猜测值将不会传递给优化器。 如果提供了 guess，则任何缺失参数的猜测值将设置为下限和上限的平均值。 必须为整数的参数的猜测值将四舍五入为整数值，并且位于用户提供的界限和分布域的交集之外的猜测值将被裁剪。

method{‘mle’, ‘mse’}

使用 method="mle" (默认)，通过最小化负对数似然函数来计算拟合。 对于超出分布支持的观察结果，应用大的、有限的惩罚（而不是无限的负对数似然）。 使用 method="mse"，通过最小化负对数乘积间距函数来计算拟合。 对于超出支持的观察结果，应用相同的惩罚。 我们遵循 [1] 的方法，该方法已针对重复观察的样本进行了推广。

optimizer可调用对象，可选

optimizer 是一个可调用对象，它接受以下位置参数。

fun可调用对象

要优化的目标函数。 fun 接受一个参数 x，即分布的候选形状参数，并返回给定 x、dist 和提供的 data 的目标函数值。 optimizer 的工作是找到最小化 fun 的决策变量的值。

optimizer 还必须接受以下关键字参数。

bounds元组序列

决策变量值的界限；每个元素将是一个包含决策变量的下限和上限的元组。

如果提供了 guess，则 optimizer 还必须接受以下关键字参数。

x0array_like

每个决策变量的猜测值。

如果分布有任何必须为整数的形状参数，或者如果分布是离散的并且位置参数未固定，则 optimizer 还必须接受以下关键字参数。

integrality布尔值 array_like

对于每个决策变量，如果决策变量必须约束为整数值，则为 True，如果决策变量是连续的，则为 False。

optimizer 必须返回一个对象，例如 scipy.optimize.OptimizeResult 的一个实例，该对象在属性 x 中保存决策变量的最佳值。 如果提供了属性 fun、status 或 message，则它们将包含在 fit 返回的结果对象中。

返回:

resultFitResult

具有以下字段的对象。

paramsnamedtuple

一个 namedtuple，其中包含分布的形状参数、位置和（如果适用）比例的最大似然估计值。

successbool 或 None

优化器是否认为优化成功终止。

messagestr 或 None

优化器提供的任何状态消息。

该对象具有以下方法

nllf(params=None, data=None)

默认情况下，给定 data 的拟合 params 处的负对数似然函数。 接受一个包含分布的替代形状、位置和比例的元组以及替代数据的数组。

plot(ax=None)

将拟合分布的 PDF/PMF 叠加在数据的归一化直方图上。

另请参阅

rv_continuous, rv_discrete

备注

当用户提供包含最大似然估计值的紧密界限时，优化更有可能收敛到最大似然估计值。 例如，当将二项分布拟合到数据时，每个样本的基础实验次数可能是已知的，在这种情况下，可以固定相应的形状参数 n。

参考文献

[1]

Shao, Yongzhao, and Marjorie G. Hahn. “Maximum product of spacings method: a unified formulation with illustration of strong consistency.” Illinois Journal of Mathematics 43.3 (1999): 489-499.

示例

在您的浏览器中尝试一下！

假设我们希望将分布拟合到以下数据。

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>> dist = stats.nbinom
>>> shapes = (5, 0.5)
>>> data = dist.rvs(*shapes, size=1000, random_state=rng)

假设我们不知道数据是如何生成的，但我们怀疑它遵循具有参数 n 和 p 的负二项分布。（参见 scipy.stats.nbinom。）我们认为参数 n 小于 30，并且我们知道参数 p 必须位于区间 [0, 1] 上。我们将此信息记录在变量 bounds 中，并将此信息传递给 fit。

>>> bounds = [(0, 30), (0, 1)]
>>> res = stats.fit(dist, data, bounds)

fit 在用户指定的 bounds 中搜索与数据最佳匹配的值（从最大似然估计的角度来看）。 在这种情况下，它找到了与实际生成数据的形状值相似的值。

>>> res.params
FitParams(n=5.0, p=0.5028157644634368, loc=0.0)  # may vary

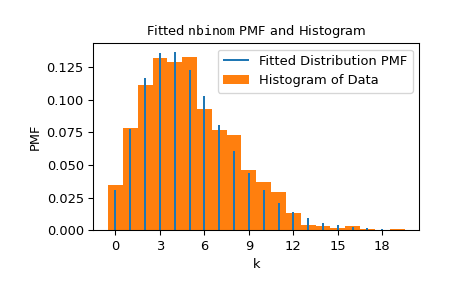
我们可以通过将分布的概率质量函数（具有拟合到数据的形状）叠加在数据的归一化直方图上来可视化结果。

>>> import matplotlib.pyplot as plt  # matplotlib must be installed to plot
>>> res.plot()
>>> plt.show()

请注意，n 的估计值正好是整数；这是因为 nbinom PMF 的域仅包含整数 n，并且 nbinom 对象“知道”这一点。 nbinom 也知道形状 p 必须是 0 到 1 之间的值。 在这种情况下 - 当分布相对于参数的域是有限的时 - 我们不需要指定参数的界限。

>>> bounds = {'n': (0, 30)}  # omit parameter p using a `dict`
>>> res2 = stats.fit(dist, data, bounds)
>>> res2.params
FitParams(n=5.0, p=0.5016492009232932, loc=0.0)  # may vary

如果我们希望强制分布以固定为 6 的 n 进行拟合，我们可以将 n 的下限和上限都设置为 6。 但是请注意，在这种情况下，通常要优化的目标函数的值会更差（更高）。

>>> bounds = {'n': (6, 6)}  # fix parameter `n`
>>> res3 = stats.fit(dist, data, bounds)
>>> res3.params
FitParams(n=6.0, p=0.5486556076755706, loc=0.0)  # may vary
>>> res3.nllf() > res.nllf()
True  # may vary

请注意，前面示例的数值结果是典型的，但它们可能会有所不同，因为 fit 使用的默认优化器 scipy.optimize.differential_evolution 是随机的。 但是，我们可以自定义优化器使用的设置以确保可重复性 - 甚至可以使用完全不同的优化器 - 使用 optimizer 参数。

>>> from scipy.optimize import differential_evolution
>>> rng = np.random.default_rng()
>>> def optimizer(fun, bounds, *, integrality):
...     return differential_evolution(fun, bounds, strategy='best2bin',
...                                   rng=rng, integrality=integrality)
>>> bounds = [(0, 30), (0, 1)]
>>> res4 = stats.fit(dist, data, bounds, optimizer=optimizer)
>>> res4.params
FitParams(n=5.0, p=0.5015183149259951, loc=0.0)

返回在新标签页中打开