scipy.stats.

rv_discrete#

class scipy.stats.rv_discrete(a=0, b=inf, name=None, badvalue=None, moment_tol=1e-08, values=None, inc=1, longname=None, shapes=None, seed=None)[源代码]#

一个用于子类化的通用离散随机变量类。

rv_discrete 是一个基类，用于构造特定分布类和离散随机变量的实例。它也可以用于构造由支持点列表和相应概率定义的任意分布。

参数:
afloat, 可选

分布支持的下界，默认值：0

bfloat, 可选

分布支持的上界，默认值：正无穷大

moment_tolfloat, 可选

用于通用矩计算的容差。

valuestuple of two array_like, 可选

(xk, pk) 其中 xk 是整数，pk 是 0 和 1 之间的非零概率，且 sum(pk) = 1。xk 和 pk 必须具有相同的形状，并且 xk 必须是唯一的。

incinteger, 可选

分布支持的增量。 默认值为 1。（尚未测试其他值）

badvaluefloat, 可选

结果数组中的值，表示违反某些参数限制的值，默认值为 np.nan。

namestr, 可选

实例的名称。 此字符串用于构造分布的默认示例。

longnamestr, 可选

当子类没有自己的文档字符串时，此字符串用作返回的文档字符串的第一行的一部分。注意：longname 存在是为了向后兼容，不要用于新的子类。

shapesstr, 可选

分布的形状。 例如，“m, n”表示将两个整数作为其所有方法的两个形状参数的分布。如果未提供，形状参数将从实例的私有方法 _pmf 和 _cdf 的签名中推断。

seed{None, int, numpy.random.Generator, numpy.random.RandomState}, 可选

如果 seed 为 None（或 np.random），则使用 numpy.random.RandomState 单例。 如果 seed 是一个 int，则使用一个新的 RandomState 实例，并使用 seed 作为种子。 如果 seed 已经是一个 Generator 或 RandomState 实例，则使用该实例。

属性:
a, bfloat, 可选

未移位/未缩放分布的支持的下/上限。 此值不受 loc 和 scale 参数的影响。 要计算移位/缩放分布的支持，请使用 support 方法。

方法

rvs(*args, **kwargs)

给定类型的随机变量。

pmf(k, *args, **kwds)

给定 RV 在 k 处的概率质量函数。

logpmf(k, *args, **kwds)

给定 RV 在 k 处的概率质量函数的对数。

cdf(k, *args, **kwds)

给定 RV 的累积分布函数。

logcdf(k, *args, **kwds)

给定 RV 在 k 处的累积分布函数的对数。

sf(k, *args, **kwds)

给定 RV 在 k 处的生存函数 (1 - cdf)。

logsf(k, *args, **kwds)

给定 RV 的生存函数的对数。

ppf(q, *args, **kwds)

给定 RV 在 q 处的百分点函数（cdf 的逆函数）。

isf(q, *args, **kwds)

给定 RV 在 q 处的逆生存函数（sf 的逆函数）。

moment(order, *args, **kwds)

指定阶数的分布的非中心矩。

stats(*args, **kwds)

给定 RV 的一些统计量。

entropy(*args, **kwds)

RV 的微分熵。

expect([func, args, loc, lb, ub, ...])

通过数值求和计算离散分布的函数相对于分布的期望值。

median(*args, **kwds)

分布的中位数。

mean(*args, **kwds)

分布的平均值。

std(*args, **kwds)

分布的标准差。

var(*args, **kwds)

分布的方差。

interval(confidence, *args, **kwds)

中位数周围具有相等面积的置信区间。

__call__(*args, **kwds)

冻结给定参数的分布。

support(*args, **kwargs)

分布的支持。

注释

此类与 rv_continuous 相似。 形状参数是否有效由 _argcheck 方法决定（默认情况下，该方法检查其参数是否严格为正。）主要区别如下。

  • 分布的支持是一组整数。

  • 此类定义了概率质量函数 pmf（以及相应的私有 _pmf），而不是概率密度函数 pdf（以及相应的私有 _pdf）。

  • 没有 scale 参数。

  • 方法（例如 _cdf）的默认实现不是为具有向下无界支持（即 a=-np.inf）的分布设计的，因此必须重写它们。

要创建一个新的离散分布，我们将执行以下操作

>>> from scipy.stats import rv_discrete
>>> class poisson_gen(rv_discrete):
...     "Poisson distribution"
...     def _pmf(self, k, mu):
...         return exp(-mu) * mu**k / factorial(k)

并创建一个实例

>>> poisson = poisson_gen(name="poisson")

请注意，上面我们以标准形式定义了泊松分布。 移动分布可以通过为实例的方法提供 loc 参数来完成。 例如，poisson.pmf(x, mu, loc) 将工作委托给 poisson._pmf(x-loc, mu)。

来自概率列表的离散分布

或者，您可以通过使用 rv_discrete 构造函数的 values 关键字参数，构造在有限值集 xk 上定义且 Prob{X=xk} = pk 的任意离散 rv。

深度复制/Pickling

如果深度复制（pickle/unpickle 等）分布或冻结分布，则任何底层随机数生成器都将与其一起深度复制。一个含义是，如果分布在复制之前依赖于单例 RandomState，则在复制后它将依赖于该随机状态的副本，并且 np.random.seed 将不再控制该状态。

示例

自定义离散分布

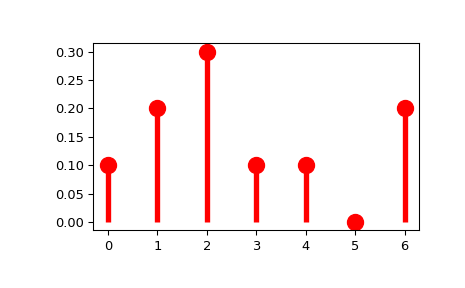
>>> import numpy as np
>>> from scipy import stats
>>> xk = np.arange(7)
>>> pk = (0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2)
>>> custm = stats.rv_discrete(name='custm', values=(xk, pk))
>>>
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.plot(xk, custm.pmf(xk), 'ro', ms=12, mec='r')
>>> ax.vlines(xk, 0, custm.pmf(xk), colors='r', lw=4)
>>> plt.show()
../../_images/scipy-stats-rv_discrete-1_00_00.png

随机数生成

>>> R = custm.rvs(size=100)
在此页面上