ecdf#
- scipy.stats.ecdf(sample)[source]#
样本的经验累积分布函数。
经验累积分布函数 (ECDF) 是样本底层分布的 CDF 的阶跃函数估计。此函数返回表示经验分布函数及其补函数(经验生存函数)的对象。
- 参数:
- sample一维类数组或
scipy.stats.CensoredData 除了类数组,还支持包含未删失和右删失观测值的
scipy.stats.CensoredData实例。目前,scipy.stats.CensoredData的其他实例将导致NotImplementedError。
- sample一维类数组或
- 返回:
- res
ECDFResult 具有以下属性的对象。
- cdf
EmpiricalDistributionFunction 表示经验累积分布函数的对象。
- sf
EmpiricalDistributionFunction 表示经验生存函数的对象。
cdf 和 sf 属性本身具有以下属性。
- quantilesndarray
定义经验 CDF/SF 的样本中的唯一值。
- probabilitiesndarray
与 quantiles 对应的概率的点估计。
以及以下方法
- evaluate(x)
在参数处评估 CDF/SF。
- plot(ax)
在提供的轴上绘制 CDF/SF。
- confidence_interval(confidence_level=0.95)
计算 quantiles 中值的 CDF/SF 周围的置信区间。
- cdf
- res
注释
当样本的每个观测值都是精确测量值时,ECDF 在每个观测值处以
1/len(sample)步进 [1]。当观测值为下限、上限或上下限时,数据被称为“删失”,并且 sample 可以作为
scipy.stats.CensoredData的实例提供。对于右删失数据,ECDF 由 Kaplan-Meier 估计量给出 [2];目前不支持其他形式的删失。
置信区间根据 Greenwood 公式或 [4] 中描述的最新“指数 Greenwood”公式计算。
参考文献
[1] (1,2,3)Conover, William Jay. Practical nonparametric statistics. Vol. 350. John Wiley & Sons, 1999.
[2]Kaplan, Edward L., and Paul Meier. “Nonparametric estimation from incomplete observations.” Journal of the American statistical association 53.282 (1958): 457-481.
[3]Goel, Manish Kumar, Pardeep Khanna, and Jugal Kishore. “Understanding survival analysis: Kaplan-Meier estimate.” International journal of Ayurveda research 1.4 (2010): 274.
[4]Sawyer, Stanley. “The Greenwood and Exponential Greenwood Confidence Intervals in Survival Analysis.” https://www.math.wustl.edu/~sawyer/handouts/greenwood.pdf
示例
未删失数据
正如 [1] 第 79 页的示例中所示,从一所高中随机选择了五个男孩。他们的一英里跑时间记录如下。
>>> sample = [6.23, 5.58, 7.06, 6.42, 5.20] # one-mile run times (minutes)
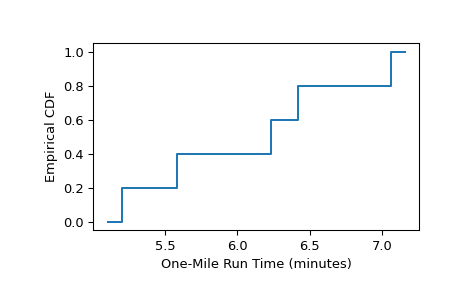
经验分布函数近似于男孩抽样人群的一英里跑时间分布函数,计算如下。
>>> from scipy import stats >>> res = stats.ecdf(sample) >>> res.cdf.quantiles array([5.2 , 5.58, 6.23, 6.42, 7.06]) >>> res.cdf.probabilities array([0.2, 0.4, 0.6, 0.8, 1. ])
要将结果绘制为阶跃函数
>>> import matplotlib.pyplot as plt >>> ax = plt.subplot() >>> res.cdf.plot(ax) >>> ax.set_xlabel('One-Mile Run Time (minutes)') >>> ax.set_ylabel('Empirical CDF') >>> plt.show()
右删失数据
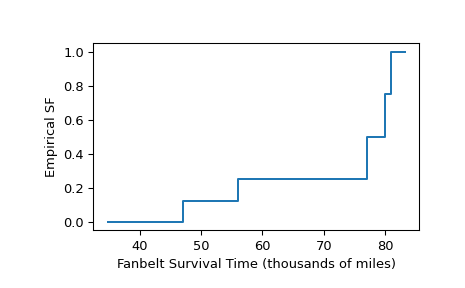
正如 [1] 第 91 页的示例中所示,测试了十个汽车风扇皮带的寿命。五个测试因被测风扇皮带断裂而结束,但其余测试因其他原因而结束(例如,研究资金耗尽,但风扇皮带仍然可以工作)。记录了风扇皮带行驶的里程如下。
>>> broken = [77, 47, 81, 56, 80] # in thousands of miles driven >>> unbroken = [62, 60, 43, 71, 37]
在测试结束时仍然可以工作的风扇皮带的精确生存时间未知,但已知它们超过
unbroken中记录的值。因此,这些观测值被称为“右删失”,并且数据使用scipy.stats.CensoredData表示。>>> sample = stats.CensoredData(uncensored=broken, right=unbroken)
经验生存函数计算如下。
>>> res = stats.ecdf(sample) >>> res.sf.quantiles array([37., 43., 47., 56., 60., 62., 71., 77., 80., 81.]) >>> res.sf.probabilities array([1. , 1. , 0.875, 0.75 , 0.75 , 0.75 , 0.75 , 0.5 , 0.25 , 0. ])
要将结果绘制为阶跃函数
>>> ax = plt.subplot() >>> res.sf.plot(ax) >>> ax.set_xlabel('Fanbelt Survival Time (thousands of miles)') >>> ax.set_ylabel('Empirical SF') >>> plt.show()