scipy.stats.

boxcox#

scipy.stats.boxcox(x, lmbda=None, alpha=None, optimizer=None)[source]#

返回通过 Box-Cox 幂变换转换的数据集。

参数:

xndarray

要转换的输入数组。

如果 lmbda 不是 None，则它是 scipy.special.boxcox 的别名。如果 x < 0 则返回 nan；如果 x == 0 且 lmbda < 0 则返回 -inf。

如果 lmbda 为 None，则数组必须为正数，一维且非恒定。

lmbda标量，可选

如果 lmbda 为 None（默认值），则找到使对数似然函数最大化的 lmbda 值，并将其作为第二个输出参数返回。

如果 lmbda 不为 None，则对该值进行转换。

alpha浮点数，可选

如果 lmbda 为 None 且 alpha 不为 None（默认值），则返回 lmbda 的 100 * (1-alpha)% 置信区间作为第三个输出参数。必须介于 0.0 和 1.0 之间。

如果 lmbda 不为 None，则忽略 alpha。

optimizer可调用对象，可选

如果 lmbda 为 None，则 optimizer 是用于查找使负对数似然函数最小化的 lmbda 值的标量优化器。 optimizer 是一个接受一个参数的可调用对象

fun可调用对象: 目标函数，它在提供的 lmbda 值处评估负对数似然函数

并返回一个对象，例如 scipy.optimize.OptimizeResult 的实例，该实例在属性 x 中保存 lmbda 的最佳值。

有关更多信息，请参阅 boxcox_normmax 中的示例或 scipy.optimize.minimize_scalar 的文档。

如果 lmbda 不为 None，则忽略 optimizer。

返回值:

boxcoxndarray: Box-Cox 幂变换数组。
maxlog浮点数，可选: 如果 lmbda 参数为 None，则第二个返回的参数是使对数似然函数最大化的 lmbda。
(min_ci, max_ci)浮点数元组，可选: 如果 lmbda 参数为 None 且 alpha 不为 None，则此返回的浮点数元组表示给定 alpha 的最小和最大置信限。

另请参阅

probplot, boxcox_normplot, boxcox_normmax, boxcox_llf

说明

Box-Cox 变换由下式给出

\[y = \begin{cases} \frac{x^\lambda - 1}{\lambda}, &\text{for } \lambda \neq 0 \log(x), &\text{for } \lambda = 0 \end{cases}\]

boxcox 需要输入数据为正数。有时，Box-Cox 变换提供一个移位参数来实现这一点； boxcox 不会。这样的移位参数等效于在调用 boxcox 之前向 x 添加一个正数常量。

提供 alpha 时返回的置信限给出了以下区间

\[l(\hat{\lambda}) - l(\lambda) < \frac{1}{2}\chi^2(1 - \alpha, 1),\]

其中 \(l\) 是对数似然函数，\(\chi^2\) 是卡方函数。

参考文献

G.E.P. Box 和 D.R. Cox，“转换分析”，皇家统计学会 B 期刊，26, 211-252 (1964)。

示例

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

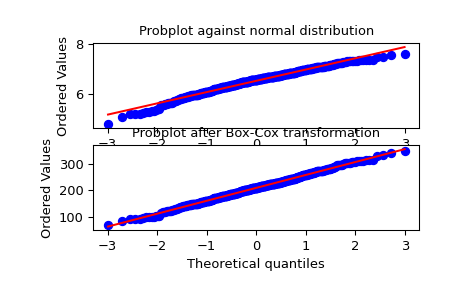
我们从非正态分布生成一些随机变量，并为其创建一个概率图，以显示它在尾部是非正态的

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

我们现在使用 boxcox 转换数据，使其最接近正态

>>> ax2 = fig.add_subplot(212)
>>> xt, _ = stats.boxcox(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Box-Cox transformation')

>>> plt.show()