scipy.special.yn#

scipy.special.yn(n, x, out=None) = <ufunc 'yn'>#

整数阶实参的第二类贝塞尔函数。

参数：

narray_like: 阶数（整数）。
xarray_like: 参数（浮点数）。
outndarray, optional: 可选的输出数组，用于存储函数结果

返回：

Y标量或 ndarray: 贝塞尔函数的值，\(Y_n(x)\)。

另请参阅

yv: 适用于实数阶和实数或复数参数。
y0: 此函数在 0 阶时的更快实现
y1: 此函数在 1 阶时的更快实现

注意

Cephes [1] 例程 yn 的封装。

该函数通过对 n 进行前向递推求值，起始值由 Cephes 例程 y0 和 y1 计算得出。如果 n = 0 或 1，则直接调用 y0 或 y1 例程。

参考文献

[1]

Cephes 数学函数库，http://www.netlib.org/cephes/

示例

在某个点计算 0 阶函数。

>>> from scipy.special import yn
>>> yn(0, 1.)
0.08825696421567697

在某个点计算不同阶数的函数。

>>> yn(0, 1.), yn(1, 1.), yn(2, 1.)
(0.08825696421567697, -0.7812128213002888, -1.6506826068162546)

通过为 v 参数提供列表或 NumPy 数组作为参数，可以在一次调用中完成不同阶数的计算

>>> yn([0, 1, 2], 1.)
array([ 0.08825696, -0.78121282, -1.65068261])

通过为 z 提供数组，在多个点计算 0 阶函数。

>>> import numpy as np
>>> points = np.array([0.5, 3., 8.])
>>> yn(0, points)
array([-0.44451873,  0.37685001,  0.22352149])

如果 z 是一个数组，则如果要在一次调用中计算不同阶数，阶数参数 v 必须可广播到正确的形状。要计算一维数组的 0 阶和 1 阶

>>> orders = np.array([[0], [1]])
>>> orders.shape
(2, 1)

>>> yn(orders, points)
array([[-0.44451873,  0.37685001,  0.22352149],
       [-1.47147239,  0.32467442, -0.15806046]])

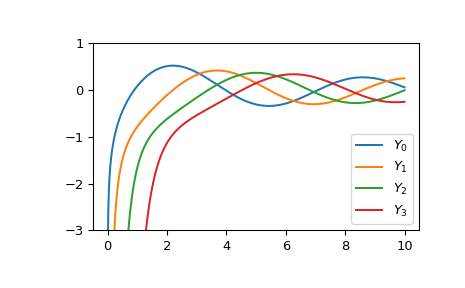
绘制 0 到 10 范围内 0 到 3 阶的函数。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 10., 1000)
>>> for i in range(4):
...     ax.plot(x, yn(i, x), label=f'$Y_{i!r}$')
>>> ax.set_ylim(-3, 1)
>>> ax.legend()
>>> plt.show()