scipy.special.kve#

scipy.special.kve(v, z, out=None) = <ufunc 'kve'>#

指数级缩放的第二类修正贝塞尔函数。

返回实数阶 v 处复数 z 的指数级缩放的第二类修正贝塞尔函数（有时也称第三类）。

kve(v, z) = kv(v, z) * exp(z)

参数:

v浮点数数组类型: 贝塞尔函数的阶
z复数数组类型: 用于计算贝塞尔函数的参数
outndarray, 可选: 可选的函数结果输出数组

返回:

标量或 ndarray: 指数级缩放的第二类修正贝塞尔函数。

另请参阅

kv: 此函数不带指数级缩放。
k0e: 此函数在阶数为 0 时的更快版本。
k1e: 此函数在阶数为 1 时的更快版本。

说明

AMOS [1] 例程 zbesk 的包装器。有关所用算法的讨论，请参阅 [2] 以及其中引用的参考文献。

参考文献

[1]

Donald E. Amos, “AMOS，一个用于复数自变量和非负阶贝塞尔函数的便携式软件包”, http://netlib.org/amos/

[2]

Donald E. Amos, “算法 644：一个用于复数自变量和非负阶贝塞尔函数的便携式软件包”, ACM TOMS Vol. 12 Issue 3, Sept. 1986, p. 265

示例

在以下示例中，kv 返回 0，而 kve 仍然返回一个有用的有限数值。

>>> import numpy as np
>>> from scipy.special import kv, kve
>>> import matplotlib.pyplot as plt
>>> kv(3, 1000.), kve(3, 1000.)
(0.0, 0.03980696128440973)

通过提供列表或 NumPy 数组作为 v 参数的实参，在单点计算不同阶数的函数

>>> kve([0, 1, 1.5], 1.)
array([1.14446308, 1.63615349, 2.50662827])

通过为 z 提供数组，在多个点计算阶数为 0 的函数。

>>> points = np.array([1., 3., 10.])
>>> kve(0, points)
array([1.14446308, 0.6977616 , 0.39163193])

通过为 v 和 z 同时提供数组，在多个点计算不同阶数的函数。两个数组都必须能够广播到正确的形状。要计算一维点数组的阶数 0、1 和 2，请执行以下操作：

>>> kve([[0], [1], [2]], points)
array([[1.14446308, 0.6977616 , 0.39163193],
       [1.63615349, 0.80656348, 0.41076657],
       [4.41677005, 1.23547058, 0.47378525]])

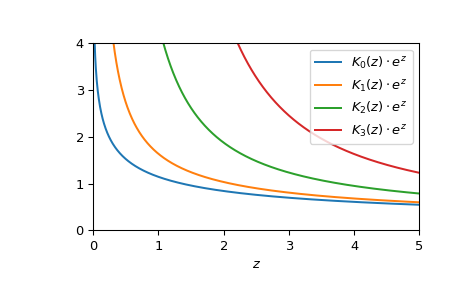
绘制阶数为 0 到 3 的函数，自变量范围从 0 到 5。

>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 5., 1000)
>>> for i in range(4):
...     ax.plot(x, kve(i, x), label=fr'$K_{i!r}(z)\cdot e^z$')
>>> ax.legend()
>>> ax.set_xlabel(r"$z$")
>>> ax.set_ylim(0, 4)
>>> ax.set_xlim(0, 5)
>>> plt.show()