scipy.special.iv#

scipy.special.iv(v, z, out=None) = <ufunc 'iv'>#

实数阶第一类修正贝塞尔函数。

参数:

v类数组: 阶数。如果 z 是实数且为负数，则 v 必须是整数值。
z浮点数或复数的类数组: 参数。
outndarray，可选: 可选的用于存放函数值的输出数组

返回:

标量或 ndarray: 修正贝塞尔函数的值。

另请参阅

ive: 此函数去除了前导指数行为。
i0: 此函数阶数为0的更快版本。
i1: 此函数阶数为1的更快版本。

注意

对于实数 z 和 \(v \in [-50, 50]\)，使用 Temme 方法 [1] 进行求值。对于更高阶数，则应用一致渐近展开式。

对于复数 z 和正数 v，调用 AMOS [2] zbesi 例程。它对小 z 使用幂级数，对大 abs(z) 使用渐近展开式，对中间幅度使用由 Wronskian 归一化的 Miller 算法和 Neumann 级数，对高阶则使用 \(I_v(z)\) 和 \(J_v(z)\) 的一致渐近展开式。必要时，使用逆向递推生成序列或降低阶数。

上述计算在右半平面进行，并通过以下公式延伸到左半平面，

\[I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\]

(当 z 的实部为正时有效)。对于负数 v，使用公式

\[I_{-v}(z) = I_v(z) + \frac{2}{\pi} \sin(\pi v) K_v(z)\]

，其中 \(K_v(z)\) 是第二类修正贝塞尔函数，使用 AMOS 例程 zbesk 进行求值。

参考文献

[1]

Temme, Journal of Computational Physics, vol 21, 343 (1976)

[2]

Donald E. Amos, “AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order”, http://netlib.org/amos/

示例

在一点处计算0阶函数。

>>> from scipy.special import iv
>>> iv(0, 1.)
1.2660658777520084

在一点处计算不同阶数的函数。

>>> iv(0, 1.), iv(1, 1.), iv(1.5, 1.)
(1.2660658777520084, 0.565159103992485, 0.2935253263474798)

可以通过为 v 参数提供列表或 NumPy 数组作为参数，一次性完成不同阶数的计算

>>> iv([0, 1, 1.5], 1.)
array([1.26606588, 0.5651591 , 0.29352533])

通过为 z 提供数组，在多个点计算0阶函数。

>>> import numpy as np
>>> points = np.array([-2., 0., 3.])
>>> iv(0, points)
array([2.2795853 , 1.        , 4.88079259])

如果 z 是一个数组，则如果要在一次调用中计算不同阶数，阶数参数 v 必须可广播到正确的形状。计算1D数组的0阶和1阶

>>> orders = np.array([[0], [1]])
>>> orders.shape
(2, 1)

>>> iv(orders, points)
array([[ 2.2795853 ,  1.        ,  4.88079259],
       [-1.59063685,  0.        ,  3.95337022]])

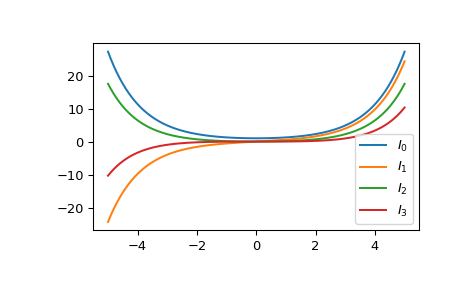
绘制从-5到5的0阶到3阶函数。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(-5., 5., 1000)
>>> for i in range(4):
...     ax.plot(x, iv(i, x), label=f'$I_{i!r}$')
>>> ax.legend()
>>> plt.show()