scipy.special.fdtri#

scipy.special.fdtri(dfn, dfd, p, out=None) = <ufunc 'fdtri'>#

F 分布的第 p 分位数。

此函数是 F 分布累积分布函数（CDF）fdtr 的逆函数，返回满足 fdtr(dfn, dfd, x) = p 的 x 值。

参数:

dfnarray_like: 第一个参数（正浮点数）。
dfdarray_like: 第二个参数（正浮点数）。
parray_like: 累积概率，范围为 [0, 1]。
outndarray, optional: 用于函数值的可选输出数组

返回值:

xscalar or ndarray: 与 p 对应的分位数。

另请参阅

fdtr: F 分布累积分布函数
fdtrc: F 分布生存函数
scipy.stats.f: F 分布

说明

该计算通过与逆正则化贝塔函数，\(I^{-1}_x(a, b)\) 的关系进行。令 \(z = I^{-1}_p(d_d/2, d_n/2).\) 则，

\[x = \frac{d_d (1 - z)}{d_n z}.\]

如果 p 满足 \(x < 0.5\)，则改为使用以下关系以提高稳定性：令 \(z' = I^{-1}_{1 - p}(d_n/2, d_d/2).\) 则，

\[x = \frac{d_d z'}{d_n (1 - z')}.\]

Cephes [1] 例程 fdtri 的包装器。

F 分布也可以通过 scipy.stats.f 获得。直接调用 fdtri 相比于 scipy.stats.f 的 ppf 方法可以提高性能（参见下面的最后一个示例）。

参考文献

[1]

Cephes 数学函数库，http://www.netlib.org/cephes/

示例

fdtri 表示 F 分布 CDF 的逆函数，该 CDF 可通过 fdtr 获得。这里，我们计算 df1=1、df2=2 且 x=3 时的 CDF 值。fdtri 然后在给定相同的 df1、df2 值和计算出的 CDF 值时，返回 3。

>>> import numpy as np
>>> from scipy.special import fdtri, fdtr
>>> df1, df2 = 1, 2
>>> x = 3
>>> cdf_value =  fdtr(df1, df2, x)
>>> fdtri(df1, df2, cdf_value)
3.000000000000006

通过为 x 提供 NumPy 数组来计算函数在多个点的值。

>>> x = np.array([0.1, 0.4, 0.7])
>>> fdtri(1, 2, x)
array([0.02020202, 0.38095238, 1.92156863])

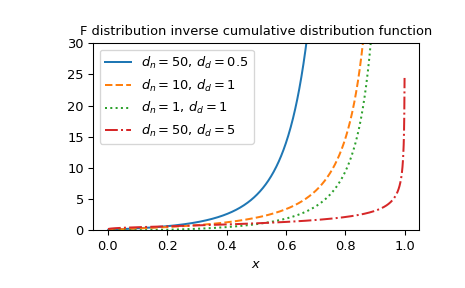
绘制不同参数集的函数图。

>>> import matplotlib.pyplot as plt
>>> dfn_parameters = [50, 10, 1, 50]
>>> dfd_parameters = [0.5, 1, 1, 5]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(dfn_parameters, dfd_parameters,
...                            linestyles))
>>> x = np.linspace(0, 1, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     dfn, dfd, style = parameter_set
...     fdtri_vals = fdtri(dfn, dfd, x)
...     ax.plot(x, fdtri_vals, label=rf"$d_n={dfn},\, d_d={dfd}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> title = "F distribution inverse cumulative distribution function"
>>> ax.set_title(title)
>>> ax.set_ylim(0, 30)
>>> plt.show()

../../_images/scipy-special-fdtri-1_00_00.png

F 分布也可以通过 scipy.stats.f 获得。直接使用 fdtri 可以比调用 scipy.stats.f 的 ppf 方法快得多，特别是对于小型数组或单个值。要获得相同的结果，必须使用以下参数化方法：stats.f(dfn, dfd).ppf(x)=fdtri(dfn, dfd, x)。

>>> from scipy.stats import f
>>> dfn, dfd = 1, 2
>>> x = 0.7
>>> fdtri_res = fdtri(dfn, dfd, x)  # this will often be faster than below
>>> f_dist_res = f(dfn, dfd).ppf(x)
>>> f_dist_res == fdtri_res  # test that results are equal
True