scipy.special.fdtr#

scipy.special.fdtr(dfn, dfd, x, out=None) = <ufunc 'fdtr'>#

F 累积分布函数。

返回 F 分布（也称为 Snedecor F 分布或 Fisher-Snedecor 分布）的累积分布函数的值。

参数为 \(d_n\) 和 \(d_d\) 的 F 分布是随机变量的分布，

\[X = \frac{U_n/d_n}{U_d/d_d},\]

其中 \(U_n\) 和 \(U_d\) 是服从 \(\chi^2\) 分布的随机变量，分别具有 \(d_n\) 和 \(d_d\) 自由度。

参数:

dfnarray_like: 第一个参数（正浮点数）。
dfdarray_like: 第二个参数（正浮点数）。
xarray_like: 参数（非负浮点数）。
outndarray, optional: 可选的输出数组，用于存放函数值

返回:

yscalar or ndarray: F 分布在 x 处的 CDF，参数为 dfn 和 dfd。

另请参阅

fdtrc: F 分布生存函数
fdtri: F 分布逆累积分布
scipy.stats.f: F 分布

说明

根据以下公式，使用正则不完全 beta 函数，

\[F(d_n, d_d; x) = I_{xd_n/(d_d + xd_n)}(d_n/2, d_d/2).\]

Cephes [1] 例程 fdtr 的包装器。F 分布也可以通过 scipy.stats.f 获得。直接调用 fdtr 相比 scipy.stats.f 的 cdf 方法可以提高性能（参见下面的最后一个示例）。

参考文献

[1]

Cephes 数学函数库, http://www.netlib.org/cephes/

示例

计算函数，当 dfn=1 和 dfd=2 时，x=1。

>>> import numpy as np
>>> from scipy.special import fdtr
>>> fdtr(1, 2, 1)
0.5773502691896258

通过为 x 提供 NumPy 数组来计算函数在多个点的值。

>>> x = np.array([0.5, 2., 3.])
>>> fdtr(1, 2, x)
array([0.4472136 , 0.70710678, 0.77459667])

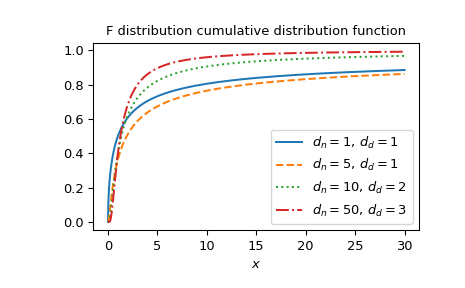
绘制不同参数集下的函数。

>>> import matplotlib.pyplot as plt
>>> dfn_parameters = [1, 5, 10, 50]
>>> dfd_parameters = [1, 1, 2, 3]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(dfn_parameters, dfd_parameters,
...                            linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     dfn, dfd, style = parameter_set
...     fdtr_vals = fdtr(dfn, dfd, x)
...     ax.plot(x, fdtr_vals, label=rf"$d_n={dfn},\, d_d={dfd}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("F distribution cumulative distribution function")
>>> plt.show()

../../_images/scipy-special-fdtr-1_00_00.png

F 分布也可以通过 scipy.stats.f 获得。直接使用 fdtr 比调用 scipy.stats.f 的 cdf 方法快得多，特别是对于小型数组或单个值。要获得相同的结果，必须使用以下参数化：stats.f(dfn, dfd).cdf(x)=fdtr(dfn, dfd, x)。

>>> from scipy.stats import f
>>> dfn, dfd = 1, 2
>>> x = 1
>>> fdtr_res = fdtr(dfn, dfd, x)  # this will often be faster than below
>>> f_dist_res = f(dfn, dfd).cdf(x)
>>> fdtr_res == f_dist_res  # test that results are equal
True