scipy.signal.

cheb1ord#

scipy.signal.cheb1ord(wp, ws, gpass, gstop, analog=False, fs=None)[源]#

切比雪夫I型滤波器阶数选择。

返回最低阶的数字或模拟切比雪夫I型滤波器的阶数，该滤波器在通带中损耗不超过 gpass dB，在阻带中衰减至少为 gstop dB。

参数:
wp, wsfloat

通带和阻带截止频率。

对于数字滤波器，这些频率与 fs 的单位相同。默认情况下，fs 为每采样2个半周期，因此这些频率被归一化到0到1之间，其中1是奈奎斯特频率。(因此 wp 和 ws 的单位是半周期/采样。)例如

  • 低通: wp = 0.2, ws = 0.3

  • 高通: wp = 0.3, ws = 0.2

  • 带通: wp = [0.2, 0.5], ws = [0.1, 0.6]

  • 带阻: wp = [0.1, 0.6], ws = [0.2, 0.5]

对于模拟滤波器，wp 和 ws 是角频率 (例如，弧度/秒)。

gpassfloat

通带中的最大损耗 (dB)。

gstopfloat

阻带中的最小衰减 (dB)。

analogbool, optional

如果为 True，则返回一个模拟滤波器，否则返回一个数字滤波器。

fsfloat, optional

数字系统的采样频率。

在 1.2.0 版本中新增。

返回:
ordint

满足要求的切比雪夫I型滤波器的最低阶数。

wnndarray 或 float

用于 cheby1 的切比雪夫自然频率（“3dB 频率”），以获得滤波器结果。如果指定了 fs，则该频率与 fs 的单位相同，并且 fs 也必须传递给 cheby1。

另请参阅

cheby1

使用阶数和临界点进行滤波器设计

buttord

根据通带和阻带规格查找阶数和临界点

cheb2ord, ellipord
iirfilter

使用阶数和临界频率进行通用滤波器设计

iirdesign

使用通带和阻带规格进行通用滤波器设计

示例

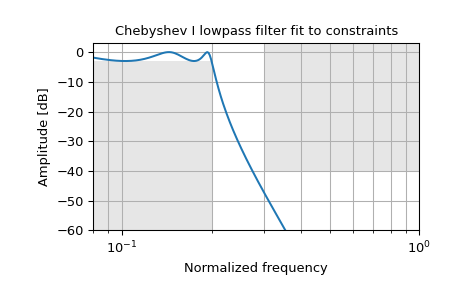
设计一个数字低通滤波器，使其通带在 0.2*(fs/2) 处不超过 3 dB 损耗，同时在 0.3*(fs/2) 以上衰减至少 -40 dB。绘制其频率响应，并用灰色显示通带和阻带约束。

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> N, Wn = signal.cheb1ord(0.2, 0.3, 3, 40)
>>> b, a = signal.cheby1(N, 3, Wn, 'low')
>>> w, h = signal.freqz(b, a)
>>> plt.semilogx(w / np.pi, 20 * np.log10(abs(h)))
>>> plt.title('Chebyshev I lowpass filter fit to constraints')
>>> plt.xlabel('Normalized frequency')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(which='both', axis='both')
>>> plt.fill([.01, 0.2, 0.2, .01], [-3, -3, -99, -99], '0.9', lw=0) # stop
>>> plt.fill([0.3, 0.3,   2,   2], [ 9, -40, -40,  9], '0.9', lw=0) # pass
>>> plt.axis([0.08, 1, -60, 3])
>>> plt.show()
../../_images/scipy-signal-cheb1ord-1.png
本页内容