scipy.signal.

buttord#

scipy.signal.buttord(wp, ws, gpass, gstop, analog=False, fs=None)[源码]#

巴特沃斯滤波器阶数选择。

返回满足以下条件的最低阶数字或模拟巴特沃斯滤波器阶数：在通带中损耗不超过 gpass dB，且在阻带中衰减至少 gstop dB。

参数:
wp, ws浮点数

通带和阻带边缘频率。

对于数字滤波器，这些频率的单位与 fs 相同。默认情况下，fs 为 2 半周期/样本，因此这些频率被归一化为 0 到 1，其中 1 是奈奎斯特频率。（wp 和 ws 因此以半周期/样本为单位。）例如

  • 低通：wp = 0.2, ws = 0.3

  • 高通：wp = 0.3, ws = 0.2

  • 带通：wp = [0.2, 0.5], ws = [0.1, 0.6]

  • 带阻：wp = [0.1, 0.6], ws = [0.2, 0.5]

对于模拟滤波器，wp 和 ws 是角频率（例如，rad/s）。

gpass浮点数

通带中的最大损耗 (dB)。

gstop浮点数

阻带中的最小衰减 (dB)。

analog布尔值，可选

如果为 True，则返回一个模拟滤波器，否则返回一个数字滤波器。

fs浮点数，可选

数字系统的采样频率。

在 1.2.0 版本中新增。

返回:
ord整数

满足规格的巴特沃斯滤波器的最低阶数。

wnndarray 或 浮点数

巴特沃斯自然频率（即“3dB 频率”）。应与 butter 一起使用以获得滤波结果。如果指定了 fs，则此频率的单位与 fs 相同，并且 fs 也必须传递给 butter。

另请参阅

butter

使用阶数和临界点进行滤波器设计

cheb1ord

根据通带和阻带规格查找阶数和临界点

cheb2ord, ellipord
iirfilter

使用阶数和临界频率进行通用滤波器设计

iirdesign

使用通带和阻带规格进行通用滤波器设计

示例

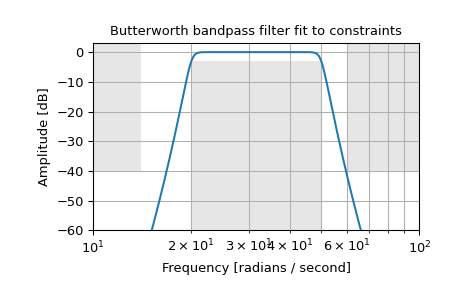
设计一个模拟带通滤波器，其通带在 20 到 50 rad/s 范围内衰减不超过 3 dB，同时在 14 rad/s 以下和 60 rad/s 以上的频率衰减至少 -40 dB。绘制其频率响应，用灰色显示通带和阻带限制。

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> N, Wn = signal.buttord([20, 50], [14, 60], 3, 40, True)
>>> b, a = signal.butter(N, Wn, 'band', True)
>>> w, h = signal.freqs(b, a, np.logspace(1, 2, 500))
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Butterworth bandpass filter fit to constraints')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(which='both', axis='both')
>>> plt.fill([1,  14,  14,   1], [-40, -40, 99, 99], '0.9', lw=0) # stop
>>> plt.fill([20, 20,  50,  50], [-99, -3, -3, -99], '0.9', lw=0) # pass
>>> plt.fill([60, 60, 1e9, 1e9], [99, -40, -40, 99], '0.9', lw=0) # stop
>>> plt.axis([10, 100, -60, 3])
>>> plt.show()
../../_images/scipy-signal-buttord-1.png
在本页