scipy.signal.

cheby1

scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba', fs=None)

切比雪夫I型数字和模拟滤波器设计。

设计一个N阶数字或模拟切比雪夫I型滤波器并返回滤波器系数。

参数:

Nint

滤波器的阶数。

rpfloat

通带中低于单位增益的最大允许纹波。以分贝为单位指定，为正数。

Wnarray_like

一个标量或长度为2的序列，给出临界频率。对于I型滤波器，这是增益首次降至-rp以下的过渡带中的点。

对于数字滤波器，Wn与fs的单位相同。默认情况下，fs为每采样2个半周期，因此这些值被归一化到0到1，其中1是奈奎斯特频率。（因此Wn的单位是半周期/采样。）

对于模拟滤波器，Wn是角频率（例如，rad/s）。

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}，可选

滤波器类型。默认为“lowpass”。

analogbool，可选

如果为True，则返回模拟滤波器，否则返回数字滤波器。

output{‘ba’, ‘zpk’, ‘sos’}，可选

输出类型：分子/分母（‘ba’）、极点-零点（‘zpk’）或二阶节（‘sos’）。为了向后兼容，默认为‘ba’，但一般用途的滤波应使用‘sos’。

fsfloat，可选

数字系统的采样频率。

在1.2.0版本中新增。

返回:

b, andarray, ndarray

IIR滤波器的分子（b）和分母（a）多项式。仅当output='ba'时返回。

z, p, kndarray, ndarray, float

IIR滤波器传递函数的零点、极点和系统增益。仅当output='zpk'时返回。

sosndarray

IIR滤波器的二阶节表示。仅当output='sos'时返回。

另请参阅

cheb1ord, cheb1ap

备注

切比雪夫I型滤波器以通带中的纹波和阶跃响应中增加的振铃为代价，最大化了频率响应通带和阻带之间的截止速率。

I型滤波器的滚降速度比II型滤波器（cheby2）快，但II型滤波器在通带中没有任何纹波。

等纹波通带具有N个最大值或最小值（例如，一个5阶滤波器有3个最大值和2个最小值）。因此，对于奇数阶滤波器，直流增益为单位增益，对于偶数阶滤波器，直流增益为-rp dB。

'sos'输出参数在0.16.0版本中添加。

示例

在浏览器中尝试！

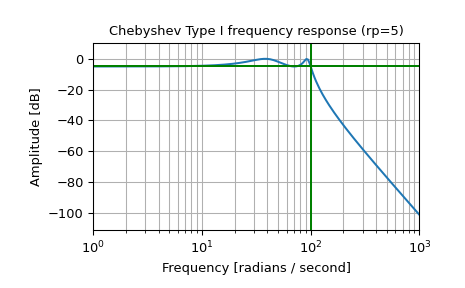
设计一个模拟滤波器并绘制其频率响应，显示临界点

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.cheby1(4, 5, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Chebyshev Type I frequency response (rp=5)')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.axhline(-5, color='green') # rp
>>> plt.show()

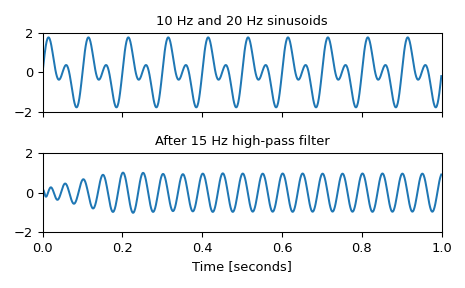
生成一个由10 Hz和20 Hz组成的信号，以1 kHz采样

>>> t = np.linspace(0, 1, 1000, False)  # 1 second
>>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
>>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
>>> ax1.plot(t, sig)
>>> ax1.set_title('10 Hz and 20 Hz sinusoids')
>>> ax1.axis([0, 1, -2, 2])

设计一个15 Hz的数字高通滤波器以去除10 Hz的音调，并将其应用于信号。（建议在滤波时使用二阶节格式，以避免使用传递函数（ba）格式时出现数值误差）

>>> sos = signal.cheby1(10, 1, 15, 'hp', fs=1000, output='sos')
>>> filtered = signal.sosfilt(sos, sig)
>>> ax2.plot(t, filtered)
>>> ax2.set_title('After 15 Hz high-pass filter')
>>> ax2.axis([0, 1, -2, 2])
>>> ax2.set_xlabel('Time [s]')
>>> plt.tight_layout()
>>> plt.show()

返回在新标签页打开